基于DEFORM的铝合金铣削有限元数值模拟

周娜，郭巨寿，王向明，卢继平

（1.中北大学机电工程学院，太原030051；2.山西柴油机工业有限责任公司，大同037036；3．北京理工大学机电一体化中心，北京100081）

基于DEFORM的铝合金铣削有限元数值模拟

周娜1，郭巨寿2，王向明1，卢继平3

（1.中北大学机电工程学院，太原030051；2.山西柴油机工业有限责任公司，大同037036；3．北京理工大学机电一体化中心，北京100081）

通过建立变厚度切削层工件模型和三维螺旋刃铣刀模型，并运用局部细化网格和自动网格划分技术对有限元模型进行处理，以达到精度和模拟时间的平衡。针对航空铝合金7050-T7451进行了两齿螺旋刃铣刀铣削加工数值模拟，并对比相同条件下的模拟结果和实验结果，对比发现铣削力和切屑形状都与实际比较一致。

变厚度切削层次摆线螺旋刃铣刀铝合金

1 前言

自1941年Martellotti详细分析铣削加工过程后指出，铣削过程中铣刀刀齿的轨迹是一条摆线，而不是圆弧线之后。Li Huaizhong等人通过建立真实的摆线轨迹模型，分析了未变形的切屑厚度，并比较了与传统近似圆弧模型之间的误差[1]。Kumanchik等人也做了类似的研究[2]。zel等人利用有限元方法研究了简化成圆弧线的刀齿运动轨迹来描述端铣（槽铣）加工过程，预测了切屑的弯曲形状、切削力和刀具应力以及切削温度等因素，并且做了实验验证[3]。简化成圆弧线的刀齿运动轨迹时着重考虑的是刀具的旋转运动，而没有考虑刀具的进给运动。因此本文在利用有限元法仿真铣削过程时，考虑了铣刀的进给运动，并实现了三维模型的次摆线轮廓。

2 铣削加工过程三维模型

2.1 次摆线工件模型的构建

刀具在铣削加工过程中，既有绕自身轴线的旋转运动，又有进给方向上的相对平移运动。铣刀刀尖可被看做从刀具中心出发的径向射线上距离旋转中心为R的某一点，切削加工时其运动轨迹形成一条次摆线，做次摆线运动的刀刃切削工件产生变厚度切屑。

让一个基圆（半径为r）在一条水平基线上做纯滚动，基圆圆弧上的某一点的轨迹为摆线，而从圆心出发的超过圆弧外的延长线上的某一点的轨迹为次摆线。铣削过程中刀尖运动的真实轨迹（摆线）所对应的参数方程为[4]如下：

其中，＋号表示逆铣；－号表示顺铣；φ为刀尖的旋转角度；R为铣刀的半径；r为基圆半径，可由下式得到：

式中，

n——铣刀转速；

T——切削时间。

将（2）、（3）代入（1）得到刀尖关于切削时间的曲线参数方程

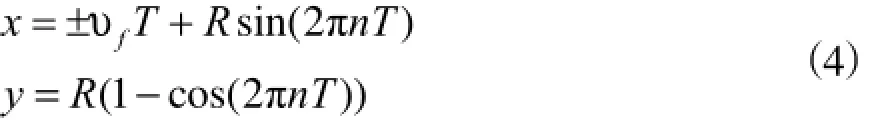
在Pro/E草图环境下插入曲线，将（4）作为笛卡儿坐标系下的曲线参数方程。由于在Pro/E中，参数t只能从0变到1，若直接将参数方程输入，则会得到铣刀刀尖旋转n圈的运动轨迹。这里我们将T=2 t/n代入参数方程，得到铣刀刀尖旋转2圈的轨迹，fn为每转进给量，如图1所示。

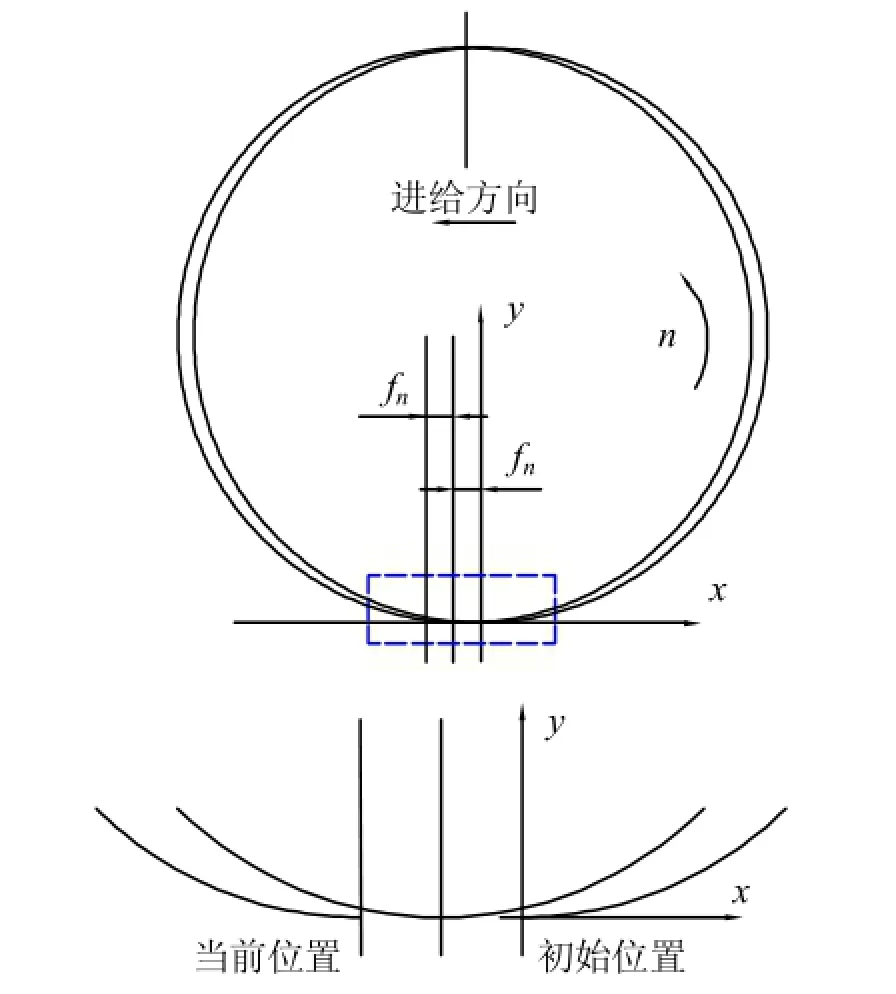
图1 铣刀刀尖次摆线轨迹示意图

铣刀刀尖的初始位置在坐标系原点处，左侧为铣刀旋转2圈后的当前位置。以此方法构建两齿铣刀刀尖切削运动轨迹，刀齿1和刀齿2刀尖轨迹所围成的部分既为边厚度切削层，切削层和工件模型见图2。

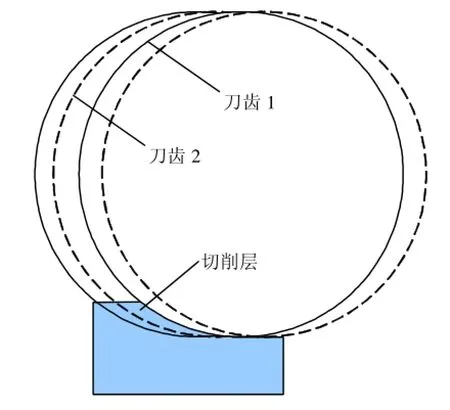
图2 次摆线工件模型及两齿铣刀切削层示意图

2.2 三维螺旋刃铣刀模型的构建

整体平头立铣刀主要由刃部、颈部和柄部三部分组成，其中，刃部是立铣刀最复杂也最关键的部分。为了满足有限元分析的需要，并且简化有限元模型，这里只对立铣刀刃部进行精确建模。其主要几何特征有刃线、前刀面、后刀面。立铣刀圆柱面上的切削刃是主切削刃，端面上分布的是副切削刃，本文研究主要研究单刃（主切削刃）切削。

本文中的立铣刀模型主要以铣刀的法前角、法后角和螺旋角为主要参数进行建模。立铣刀法前角20°，法后角20°，螺旋角20°，直径为20 mm。平头立铣刀的刃线是一条以特定螺旋角沿柱面上升的螺旋线，可通过pro/E插入基准曲线得到。根据螺旋线理论，常螺旋线方程为

而螺旋线在Pro/e中笛卡尔坐标系下的参数方程为

其中，R为铣刀半径，φ为铣刀螺旋角，t为参数，m=2πRcotφ。

在传统的平面设计中，一般是按容屑槽的端截面进行截形设计，将导致在法向截面内不能成功地保证齿刃前刀面的直线形状和容屑槽底的圆弧。本文在得到立铣刀刃线之后，进行扫描混合建立刃部实体。建模步骤如下：垂直刃线轨迹草绘第一个立铣刀法向截面（见图3），在刃线旋转过90°时，草绘第二个法向截面并旋转90°，得到立铣刀切削刃实体模型。这样就保证了立铣刀刃部法向截形的准确形状。

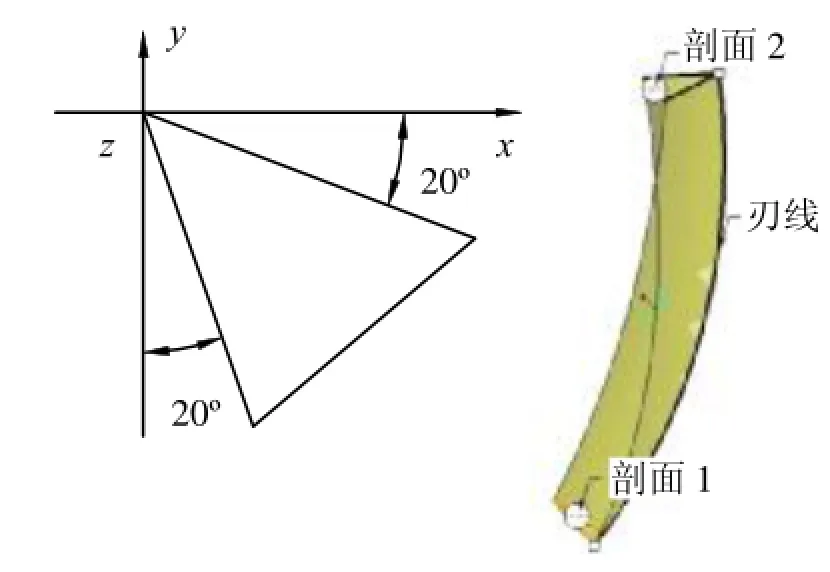
图3 立铣刀刃部法向截形及切削刃模型

最终得到的两齿立铣刀模型如图4。从图中可以看出铣刀芯部较真实铣刀芯部单薄，这是因为在有限元分析过程中刀具设为刚体，为了尽量减少网格数量，减少计算时间，将芯部做适当简化，只精确画出了参与切削的切削刃。

图4 立铣刀简化模型

值得注意的是，在工件的三维造型中，切屑的外轮廓线是一条次摆线，且尺寸较小，以Pro/E默认精度拟合的曲线会切削层理论值产生较大的几何失真。为了保证仿真精度，应适当调整Pro/E的系统精度。另外，从Pro/E三维造型环境中保存*.stl格式文件导入DEFORM有限元仿真环境时，可将偏差控制值设置的尽可能小，以保证三维模型的几何形状精度。建模时的默认参考系也一并引入到DEFORM的装配环境中，为了装配方便，最好在建模时考虑好工件和刀具坐标系的装配关系。

3 有限元网格划分策略

在划分网格时，网格数量要综合考虑计算精度和计算时间问题。单元格数量不宜过多，过多的单元格会造成运算时间呈指数上升，大大增加计算成本。再考虑到计算机字长和计算机舍入误差的存在，若网络划分太密，反而会引起误差的累加。

对于本例来说，在前处理中完成网格划分生成数据库文件后，三维实体模型即被删除，只剩下对实体结构近似逼近的有限元网格结构。此时，原切削层的理论轮廓（曲线）被有限元网格结构形成的切削层轮廓（直线段逼近的曲线）所代替，这不可避免的再一次产生几何失真。当切削仿真开始以后，网格畸变到一定程度时会激发网格重划分，每一次重划分所用的几何模型都是从上一次网格划分后形成的有限元网格结构模型提取的。经过多次的网格重划分和结构逼近后，几何误差会不断积累，从而导致尺寸微小的切削层形状产生失真，最终导致切屑厚度和计算结果明显偏离理论值。这些偏差给精加工切削仿真带来了困难，因为通常情况下精加工的进给量和切削深度非常小，仿真过程中有限元网格重划分后形成的几何模型会产生严重畸变，很容易使切削参数偏离预定值。

为了避免这种情况，就需保证切削层边缘上的节点数足够多，才能减小切削层轮廓曲线的失真，基于这种考虑需保证网格细化中曲率权重因子的大小。通过仿真对比发现，各网格细化权重因子保持默认值，利用软件本身的网格动态自适应的功能，基本可以满足要求。如果要使切削层的几何精度和切屑的形状来达到更高的精度，可以利用固定的网格细化窗口将理论切削层和生成的切屑所在空间进行适当的局部网格细化。也可采用随刀尖运动的网格细化窗口来细化网格，不过运动的局部网格细化会不断激发网格重划分，在网格细化窗口内可能会产生不必要的细化网格。另外，在仿真过程中，由于切屑与工件的分离和变形使得工件模型几何形状严重不规则化，使精细网格划分增大难度，增加每一次网格划分的时间，从这方面考虑不建议采用运动的网格细化设置[5]。

网格尺寸比例“size ratio”设置不宜过高，通常取值在7（软件切削例子所用值）左右即可，可根据模型的复杂程度作适当调整。设置过大的“size ratio”值，会出现局部网格粗大，容易引起几何模型失真。

对于真实轨迹的铣削加工来说，切屑为变厚度切屑，切削层厚度由非零逐渐减小为零的。而有限元法本身就是对实际结构的近似逼近，所以在切削层厚度由零变为非零的过程中，当切削层的单元格最小长度大于于切屑厚度时，无论是逆铣还是顺铣，仿真过程都不可能产生无切屑，这给仿真过程带来了一定的误差。为了最大程度的减小这种误差，可以在切削层厚度较小处进行网格局部细化来缩小单元格的最小边长，或者在三维建模时将此部分实体删掉，以得到更接近于理论长度的切屑。

4 模拟结果与实验对比

工件材料为铝合金7050-T7451，采用文献[5]给出的材料本构关系模型。模拟时刀具从图4所示位置开始切削铣削加工。模拟条件为：转速8 000 r/min，进给速度6 000 mm/min，切削宽度4.3 mm，切削深度3.42 mm；采用二齿整体硬质合金立铣刀，牌号为K10，弹性模量为600 GPa，刀具直径20 mm，前角20°，后角20°，螺旋角20°。工件材料弹性模量69 GPa，泊松比0.33。

图5分别示出了刀具在切入和切出某时刻的刀具和工件的相互作用及切屑形状以及实际加工得到的切屑形状，可见模拟得到的切屑和实际切屑极为相似。

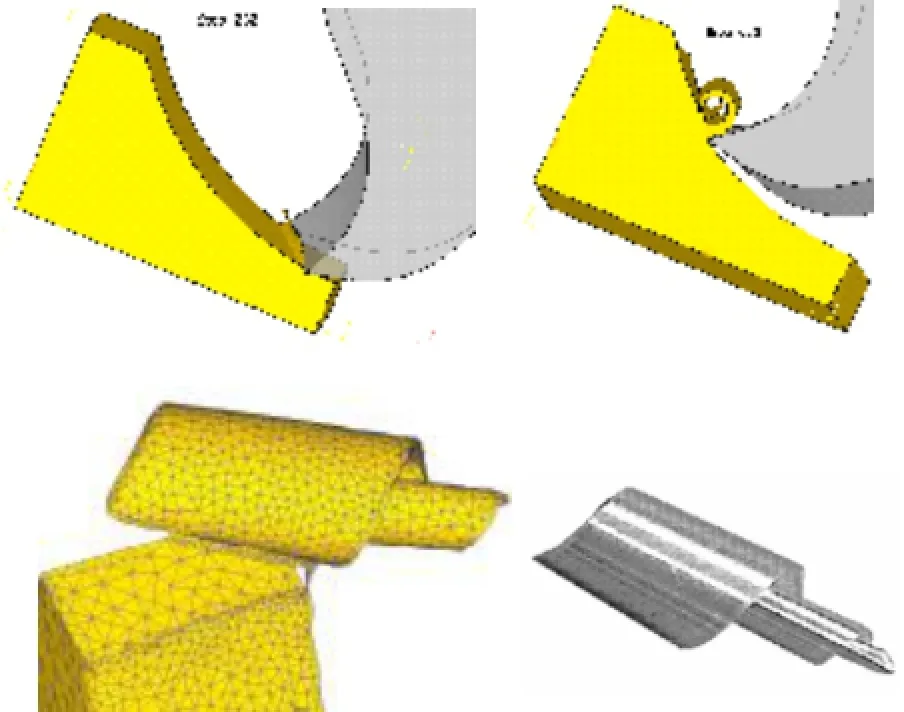
图5 切屑形成过程及实际切屑对比

图6为三向切削参数对应的切削力曲线，图中曲线对应于刀具切削工件时的一个切削周期刀具的连续切削则是此切削周期的不断重复。比较实测和模拟得到的切削力曲线可知，两者的切削力随时间的变化趋势基本是一致的。其中切削力的载荷相差较大，分析原因可能为材料本构关系模型有待改进。表1给出了切削力的模拟值和实测值的对比及其误差。

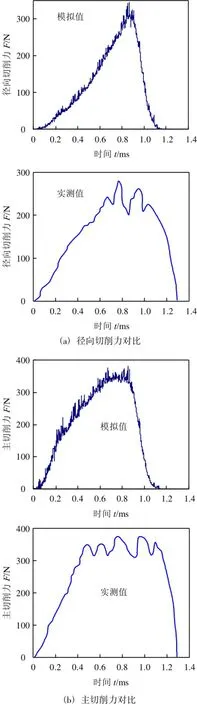
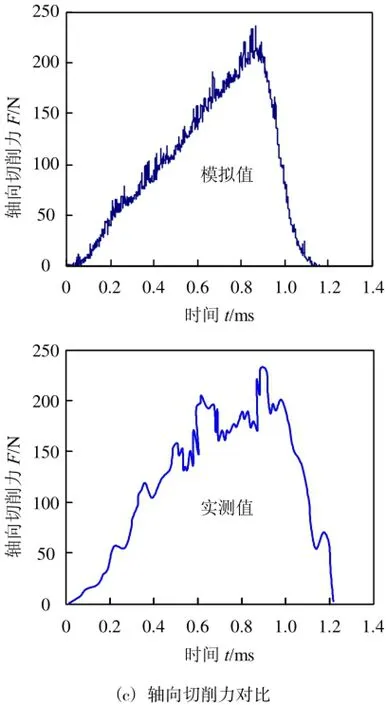
图6 模拟切削力与实测值对比

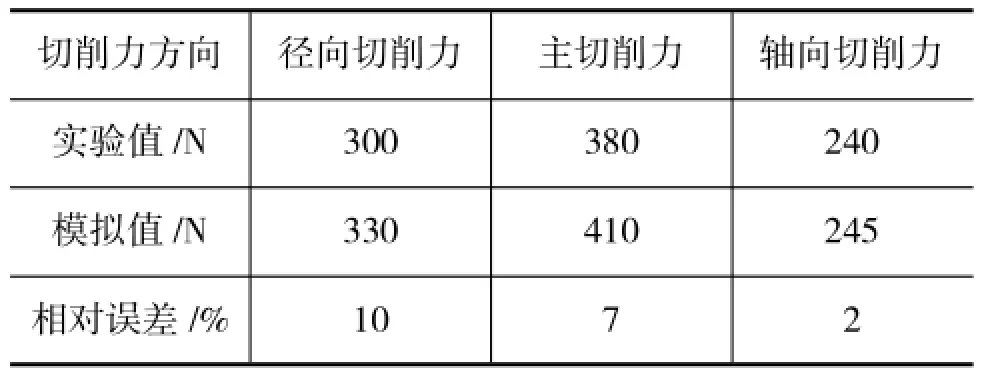
表1 切削力模拟误差对比

图7为采用等效厚度法得到的切削力曲线，从图中可以看说，三个方向的切削力趋势都是上升到最大值后保持恒定，不能体现真实切削过程中任意时刻的切削大小。

5 结论

（1）建立了螺旋齿单刃斜角铣削有限元模型，该模型可用于预测不同切削参数组合下的铣削力，给实际加工刀具集合参数、切削用量选择、机床选用等提供参考。同时，模拟得到的切屑与实际切屑也很相似。

（2）为高强度铝合金铣削加工数值模拟的深入研究奠定了基础。通过组合不同的切削参数分别进行模拟，可得到优化的切削参数；通过组合不同的刀具材料和刀具几何尺寸分别进行模拟，可辅助切削加工刀具的优选和优化设计，从而减小切削加工刀具的磨损，提高刀具使用寿命。

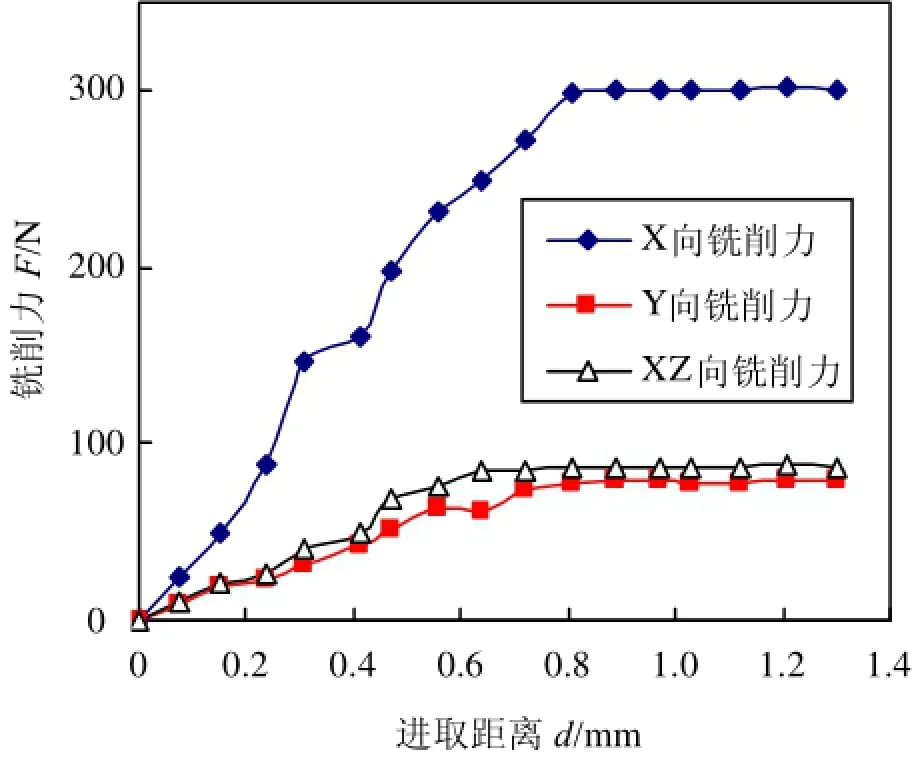
图7 斜角等效厚度切削层法得到的切削力曲线

1 Li H Z,Liu K,Li X P.A New Method for Determining the Undeformed Chip Thickness in Milling[J].Journal of Materials Processing Technology,2001,113(1～3):378-384.

2 Kumanchik L M,Schmitz T L.Improved Analytical Chip Thickness Model for Milling[J].Precision Engineering,2007,31(3):317-324.

4袁平，柯映林，董辉跃．基于次摆线轨迹的铝合金高速铣削有限元仿真[J]．浙江大学学报（工学版），2009，43（3）：570-577．

5吴红兵，柯映林，刘刚等．航空铝合金高速铣削加工的三维数值模拟[J]．浙江大学学报（工学版），2008，42（2）：234-238．

Numerical Simulation of Aluminum Alloy Milling Based on DEFORM Finite Element

Zhou Na1,Guo Jushou2,Wang Xiangming1,Lu Jiping3
（1.Electromechanical Engineering College,North University Of China,Taiyuan 030051,China; 2.Shanxi Diesel Engine Industries Corporation.LTD,Datong 037036，China; 3.Mechatronics Centre of Beijing Institute of Technology,Beijing 100081,China）

To get balance between the accuracy and the simulated time,the paper established models of variable thickness cutting layer work and three-dimensional spiral milling cutter.Partial refining grid and automatic grid divided technology was used in the processing of models.Furthermore,numerical simulation on bi-gear spiral milling cutter milling was done to the aerolite 7050-T7451.From the simulation and experimental results in the same condition,concordance between milling force and chipping shape was gained lastly.

variable thickness cutting layer,trochoid,spiral milling cutter,aluminum alloy

10.3969/j.issn.1671-0614.2013.03.009

来稿日期：2013-05-27基金项目：国家自然科学基金资助项目（51275489）

周娜（1986-），女，硕士，主要研究方向为发动机总体设计。