基于热机耦合的缸套变形分析

朱小平，白曙，陈阳，宋红年

（上海柴油机股份有限公司，上海200438）

基于热机耦合的缸套变形分析

朱小平，白曙，陈阳，宋红年

（上海柴油机股份有限公司，上海200438）

采用热机耦合分析方法，对柴油机气缸套进行了温度场分析，并将温度场用于耦合场的计算,分析了不同载荷对气缸套变形的影响。计算结果表明：气缸套最高温度为230.6℃,出现在缸套内壁顶部；缸套变形总体符合要求。热载荷是气缸套变形的主导因素，控制缸套变形时应主要控制热载荷引起的变形，对指导气缸套的设计具有重要意义。

气缸套温度场耦合场变形

1 前言

气缸套是发动机的重要零件之一，它对活塞起支承和导向作用。气缸套在受到螺栓预紧力及活塞侧向力等机械应力作用时候会产生一定的机械变形，而其内壁受到高温高压燃气作用，燃烧过程中燃气的最高温度可达2 500℃左右，外侧被冷却水包围，温度不高于100℃，如此大的内外壁温差将导致气缸套有很大的热变形[1]。

气缸套变形过大将导致活塞环与气缸套壁面之间不能良好地接触而出现间隙，燃气会从间隙处泄露出来，导致做功的燃气减少，输出功率降低，燃油消耗率增加。同时，机油也容易从间隙处蹿入燃烧室，在高温下裂解甚至燃烧，产生大量有害颗粒，影响排放。气缸套变形过大还会导致气缸垫密封失效，缸套磨损、机油消耗大等质量及可靠性的问题[2]。

随着柴油机的强化程度越来越高，最大爆发压力和平均有效压力均提高，需要更大的螺栓预紧力来压紧气缸盖垫片和缸套。而螺栓预紧力中50%～70%均作用在缸套上，这将导致发动机缸套孔变形变得更加严重。而现代发动机的轻量化要求也日益提高，使得发动机的结构更加紧凑；又由于缸套薄壁结构的特点以及与之相连接的机体刚度差异，导致发动机的气缸孔更容易变形。因此，对发动机气缸孔变形的研究将越来越重要，必须保证气缸孔的变形在合理的范围内。

本文以某机型为研究对象，采用热机耦合的方法，对气缸套的温度场和变形进行了模拟计算，对缸套变形的影响因素进行了分析，从而为缸套的设计和检验提供了参考。

2 计算方法和仿真模型的建立

2.1 计算方法

柴油机在运行时，气缸套承受着装配载荷、热载荷和燃气压力载荷。因此，对气缸套变形做出正确的评价需要考虑热载荷和机械载荷同时作用下的气缸套的应力状态，即热机耦合下的应力状态。

热载荷通过热传递分析得到，因此气缸套的变形计算可分为2个主要步骤，即热传递分析和结构分析。

热结构耦合方法分为顺序耦合和直接耦合。本文计算中选用更方便、更灵活的顺序耦合分析方法：首先对模型施加热分析的初始条件和边界条件，计算得到模型的温度场结果；然后把模型的节点温度作为结构分析的耦合载荷与结构分析的边界条件一起施加到模型上，得到结构分析的应力场结果[3]；最后提取变形结果对缸套的变形进行分析评价。整个分析流程如图1所示。

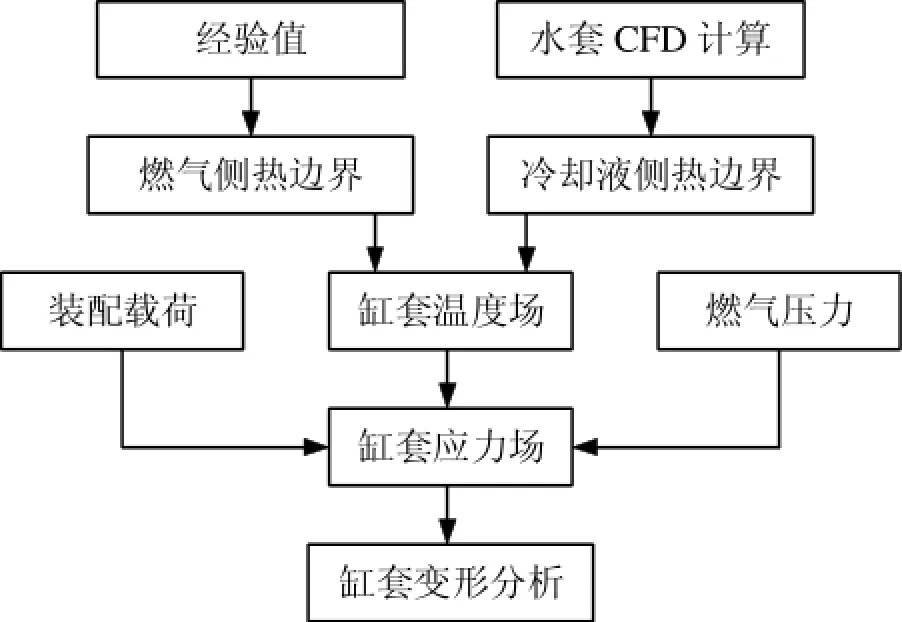
图1 气缸套变形分析流程

2.2 气缸套仿真模型的建立

本次分析对象为某6缸柴油机。为使计算准确，建立了中间2、3和4缸的有限元模型。

整体模型包括缸盖、机体、缸垫、缸盖螺栓、气门座圈和缸套。计算中考虑材料属性随温度的变化。限于篇幅，表1仅列出主要部件在20℃常温下的材料属性。

有限元网格的划分需要考虑单元类型和单元数量方面的问题。气缸盖和机体结构非常复杂，因此本文采用二阶四面体单元进行建模，对重要区域进行网格细化，建立的模型如图2所示。

3 有限元计算的边界条件

3.1 温度场计算边界条件

本文应用有限元法对气缸套温度场进行计算分析时采用第三类热边界条件，即给定温度和换热系数。缸套温度场计算热边界条件，包括冷却水侧和燃气侧。冷却水侧由CFD软件计算得到，即首先对发动机冷却水套进行流动和传热分析，然后将气缸套侧水腔表面的温度值和换热系数映射到气缸套水腔壁面上，从而完成对其热边界的施加；缸套燃气侧中，活塞下止点以上部分的稳态传热热边界条件沿轴向高度上有如下分布规律[4]：

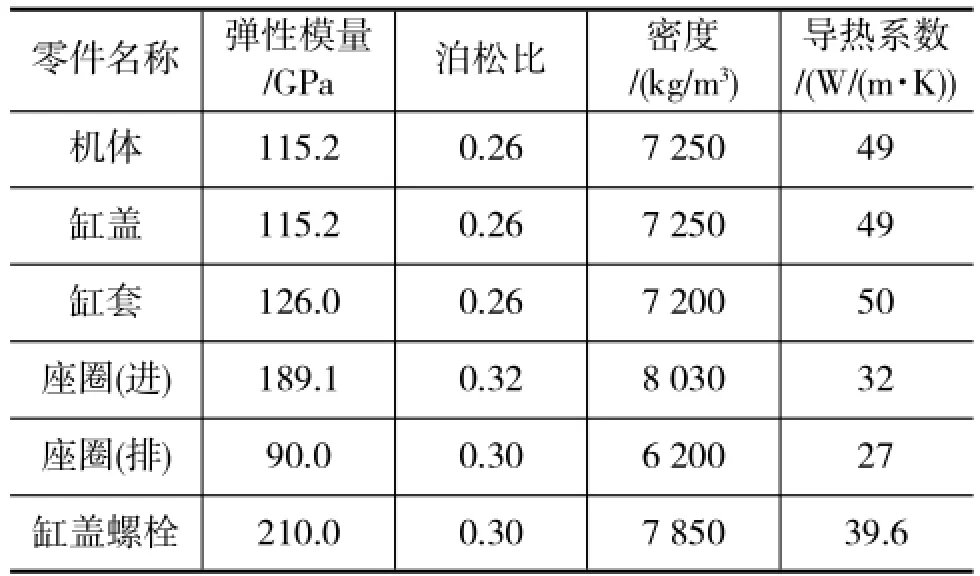
表1 主要零件材料属性表

图2 气缸套有限元分析模型

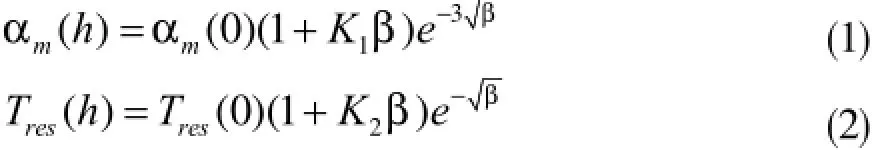
活塞下止点以下部分不与燃气接触，换热量小很多，热边界条件沿轴向高度上有如下分布规律：

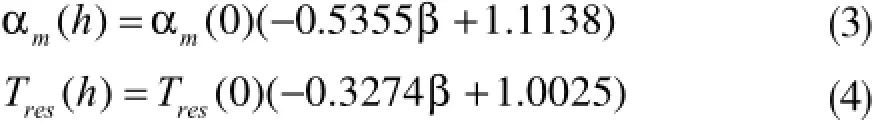
式中，

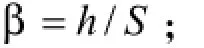
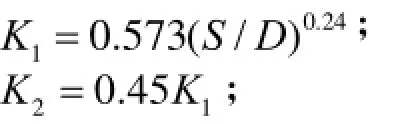
αm(0)和Tres(0)分别对应柴油机工作循环中燃气的平均换热系数和平均温度；

S——行程；

D——缸径。

根据以上经验公式，计算得到燃气测的温度和换热系数，再结合本次计算的具体机型，设定如表2所示的热边界条件。

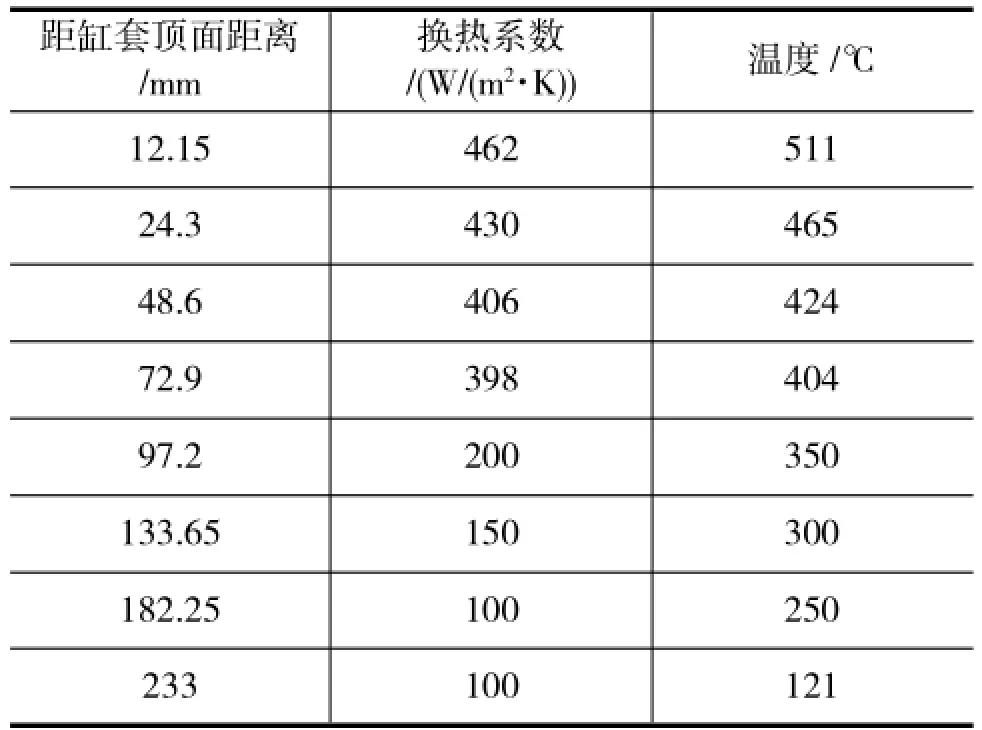
表2 燃气侧的热边界条件

3.2 耦合场计算边界条件

（1）载荷边界条件：载荷边界条件主要为装配拧紧载荷和爆发压力，缸盖螺栓拧紧采用扭矩转角法，拧紧力矩为115±5 N·m，转角为95±5°，最大爆压为16 MPa。

（2）位移边界条件：位移约束边界包括计算模型前后端两侧截面的对称约束和机体底面的全约束边界。

（3）温度边界条件：温度边界条件即由热边界计算得到的温度场结果。进行耦合计算时将温度场的结果加载到有限元模型的各个节点上。

4 计算结果与分析

4.1 温度场计算结果

图4为缸套整体温度场的计算结果。由图中可以看出，缸套最高温度值出现在顶面区域，最大值为230.6℃，符合材料许可温度的要求。

本文重点考察中间第3缸。图5为第3缸缸套内壁轴向温度变化的分布图，横坐标表示距缸套顶面距离与缸套总高的比值（无量纲轴向高度）。可以看出活塞顶上面的缸套区域因直接暴露在燃气中，受燃气的冲刷，且不处于冷却水套区域，所以导致该区域温度比较高。冷却水套区域受冷却水冲刷的作用，温度较低。图6为缸套内壁靠近第1道活塞环高度上径向截面节点的温度变化图，横坐标表示径向各节点与选取的第1个节点间径向弧长与总弧长的比值。由图中可以看出最高温度低于165℃。将各节点温度均值处理后得到平均温度为148℃，满足温度许可要求。

图4 缸套温度场分布图

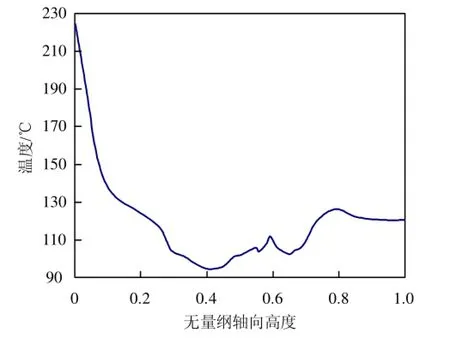
图5 缸套内壁面的轴向温度

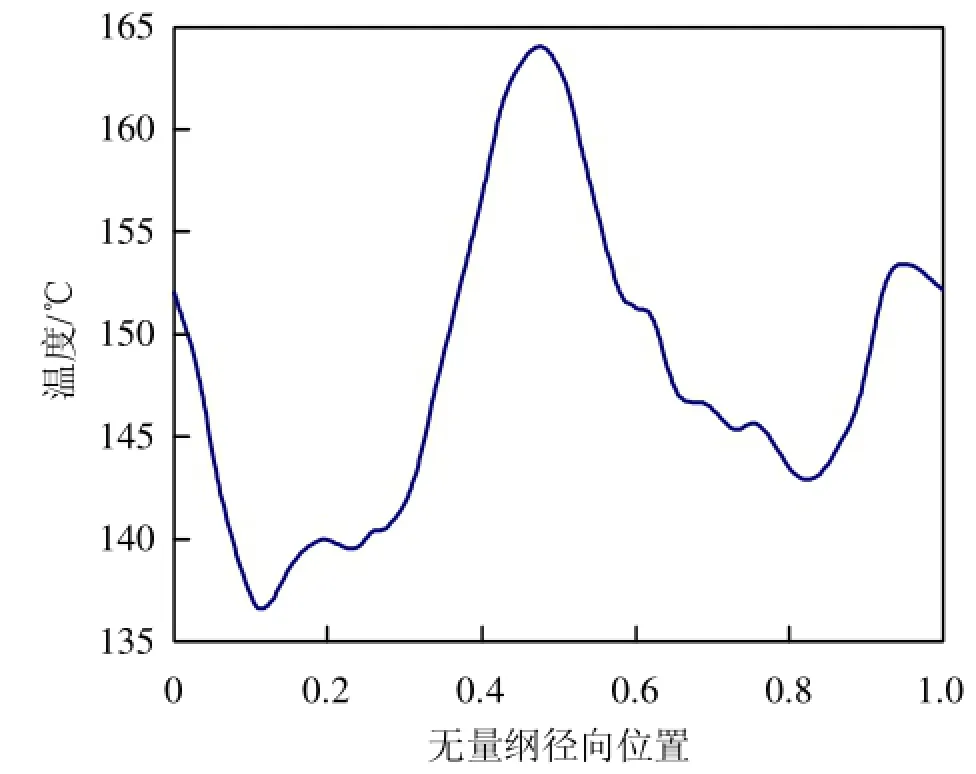
图6 缸套内壁面第1道活塞环高度上径向温度

4.2 耦合场变形分析

缸套变形主要通过整体变形、轴向变形和径向变形3种评价指标进行分析。

为考察不同因素对气缸套变形的影响，本文共计算了3个工况：装配载荷工况（LC1）、装配载荷叠加热载荷工况（LC2）、在LC2工况基础上对第3缸施加爆压工况（LC3）。

4.2.1 缸套总体变形分析

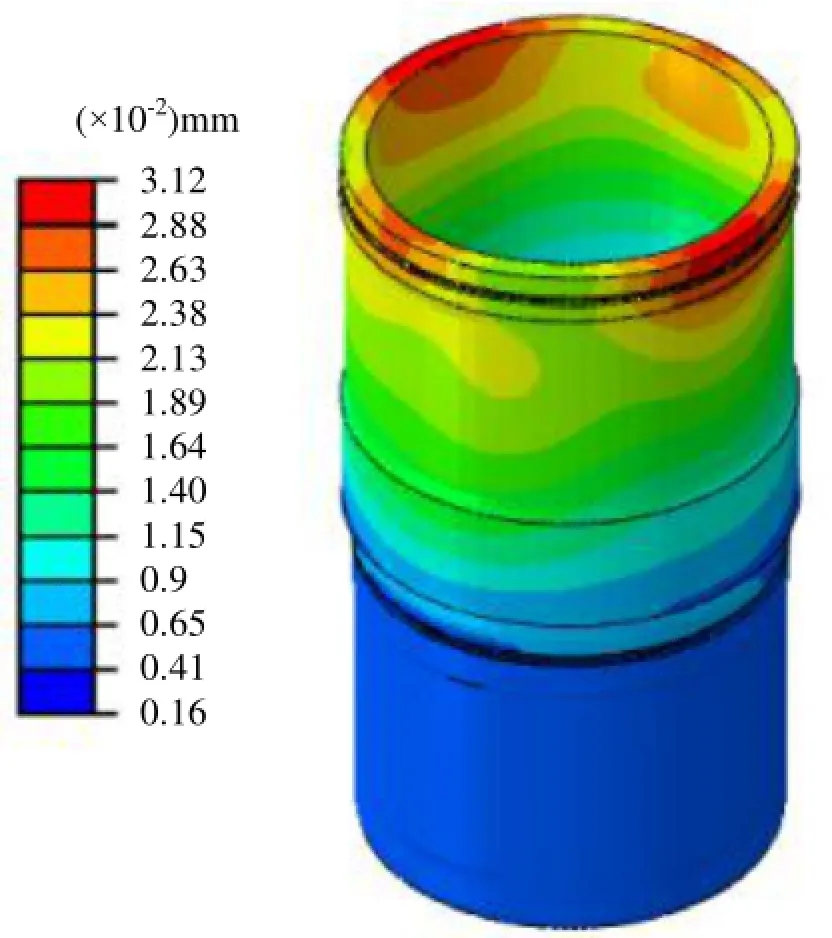
图7 工况1下缸套总体变形

图8 工况2下缸套总体变形

图9 工况3下缸套总体变形

图7～图9为缸套在3个工况下的总体变形，变形放大系数为100。由图中可以看出，LC1工况下最大变形量为0.031 26 mm，LC2工况下最大变形量为0.344 5 mm，LC3工况下最大变形量为0.408 2 mm。LC2和LC3这2个工况的变形类似。这说明在多种载荷作用下，热载荷对缸套变形起主要作用。

4.2.2 缸套轴向变形分析

如图10所示选取4个角度分析缸套的轴向变形，图11～图14为缸套各个角度对应轴向在3个不同的工况下的变形分布图。

由图中可以看出，在LC1工况下，缸套的变形在4个角度下均比较小。螺栓预紧力主要对缸套上部变形有较大的影响，沿着缸套轴向向下影响变小。在LC2工况下，缸套变形明显加大；且90°和270°对应轴向变形更加明显。LC3工况下的变形与LC2工况相似，主要对缸套顶部的变形影响较大，沿着缸套轴向向下影响变小。

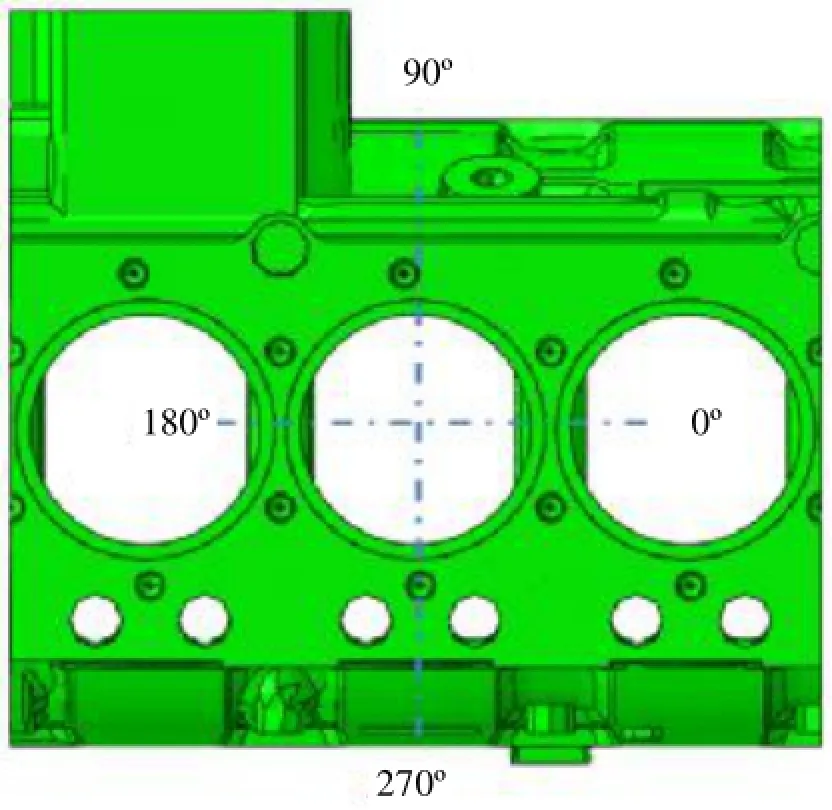
图10 缸套各轴向角度示意图

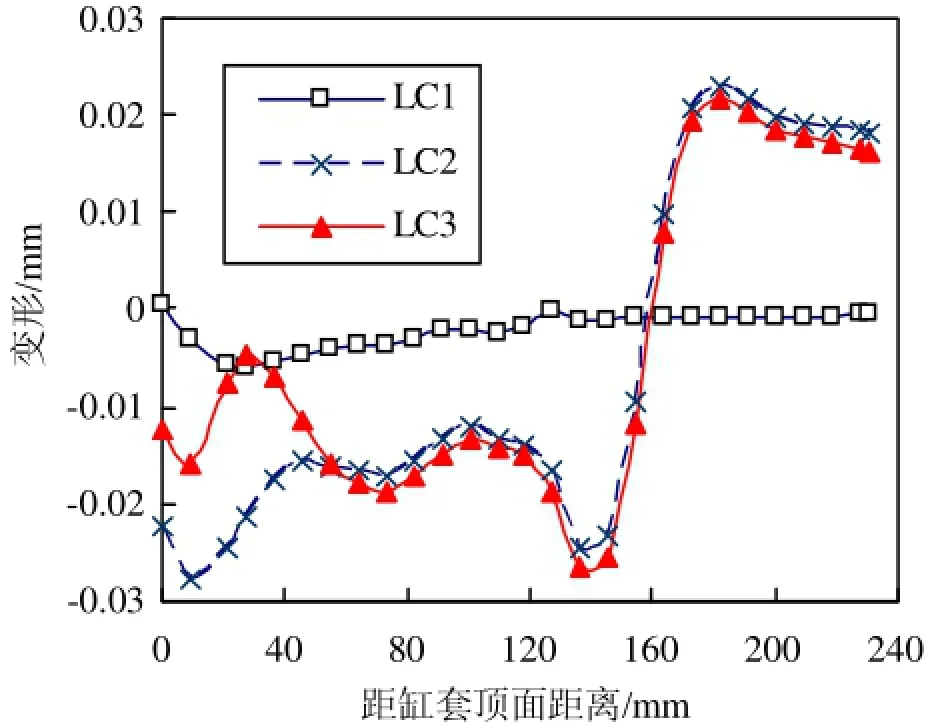
图11 缸套0°对应轴向变形图

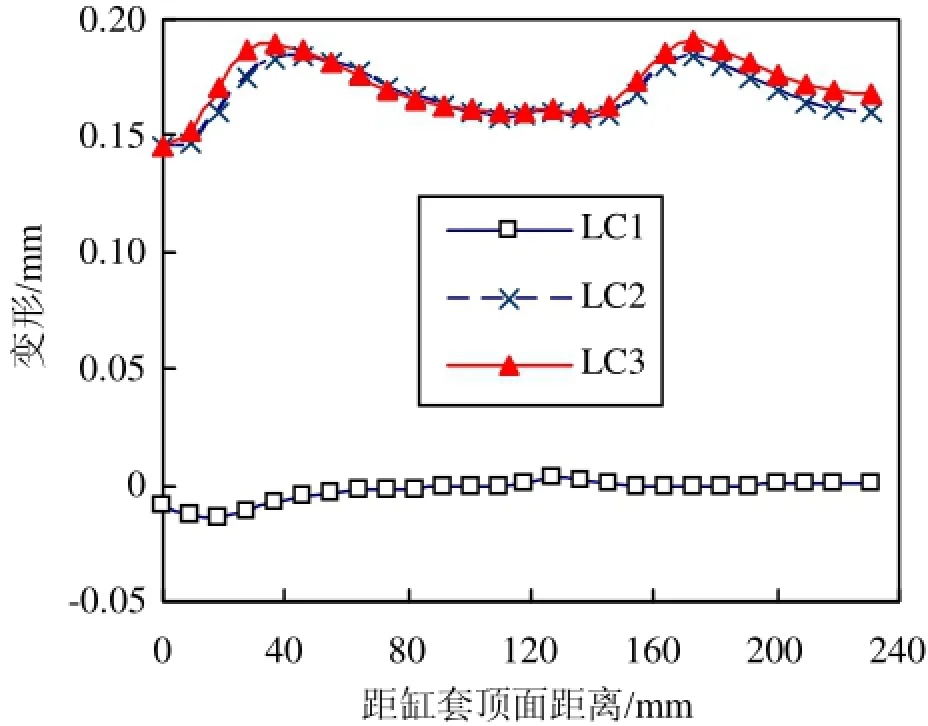
图12 缸套90°对应轴向变形图

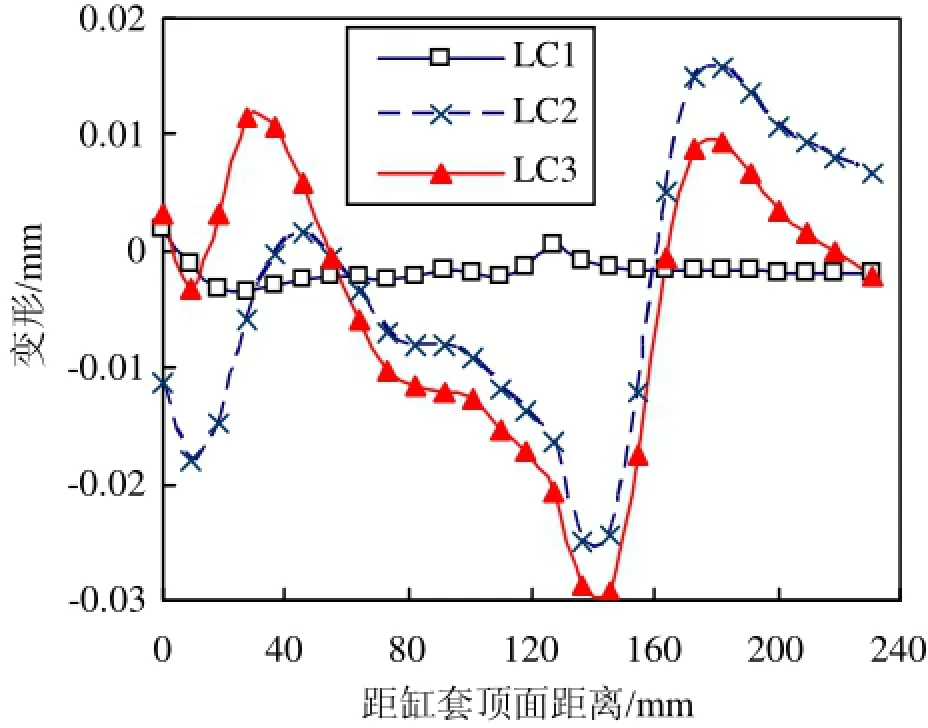
图13 缸套180°对应轴向变形图

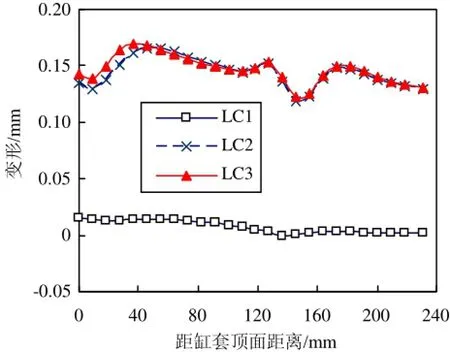
图14 缸套270°对应轴向变形图

4.2.3 缸套径向变形分析

缸套的径向变形分析也就是缸孔的失圆度分析。可根据计算结果取不同高度的缸孔变形曲线在极坐标下分析其径向的变形，也可借用谐波的概念对这些变形“圆”进行分析，应用快速傅里叶变换（FFT）计算不同阶次下的变形[5]。

根据变形出现的条件，可以将变形分为静态变形和动态变形。0、1、4阶变形为静态变形；2、3阶及更高阶次数的变形为动态变形。0、1阶变形主要是由制造公差和装配公差引起的整体尺寸和位置上的变化[6]。在本次计算中，主要考虑2～8阶变形。

选取缸套关键横截面进行分析，如表3所示。将各截面在装配工况下的径向变形进行傅里叶变换，得到如图15所示的结果。

各阶次下变形限值可按下式进行计算：

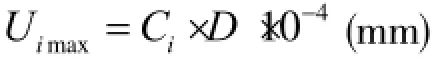
其中，Uimax为各阶次下变形的最大值，Ci为系数，D为缸径，各阶所对应的Ci值如表4所示。

根据表4计算得到本机型在各阶次下变形限值，如表5所示。由此得出，缸套径向变形符合要求。

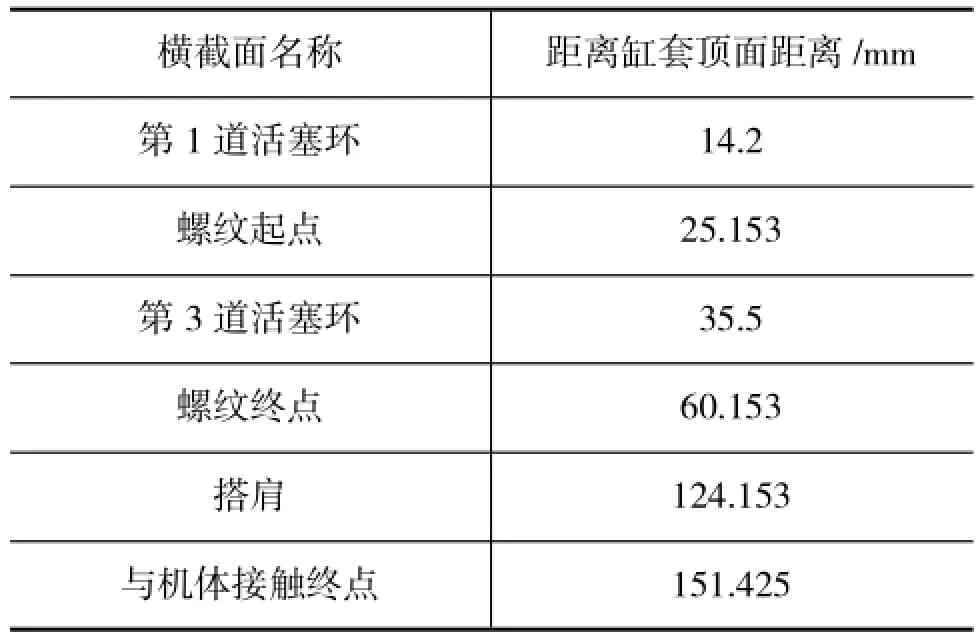
表3 各横截面定义

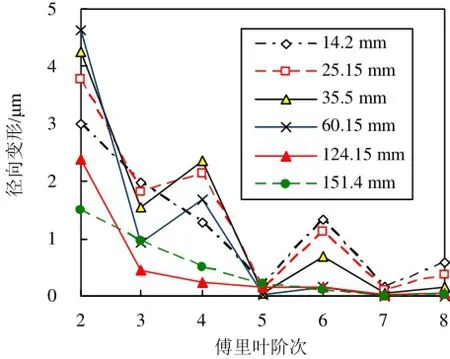
图15 缸套关键截面各阶下径向变形图

表4 各阶下对应的Ci值

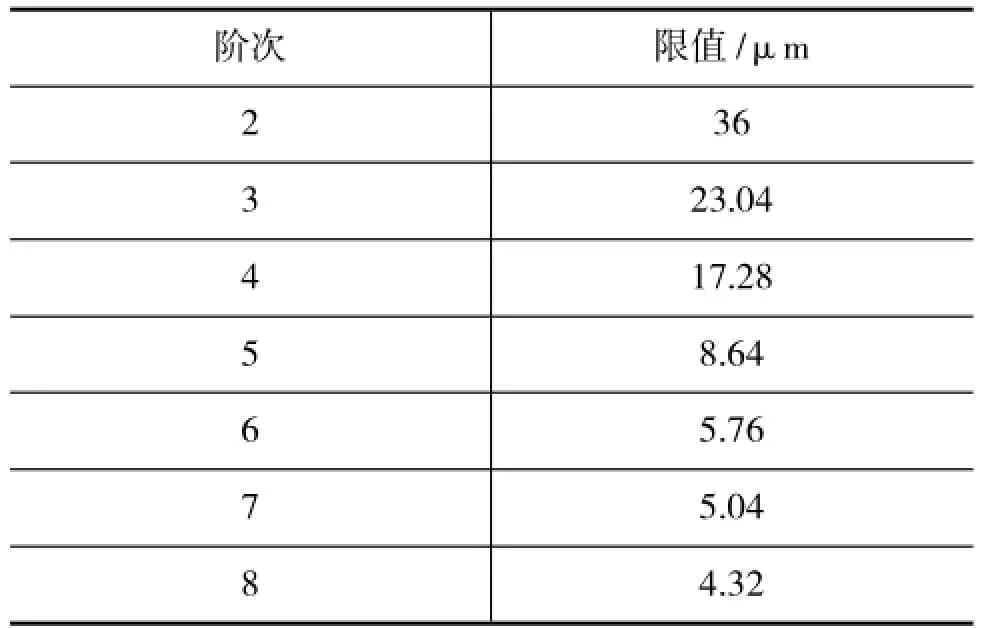
表5 各阶次下对应的变形限值

5 结论

本文通过热机耦合的方法计算了缸盖的温度场和分析了缸套的变形，结论如下：

（1）缸套最高温度为230.6℃，出现缸套顶部，满足材料许可温度的要求；缸套内壁靠近第,1活塞环径向节点温度均值为148℃，满足要求。

（2）根据耦合场计算结果取出了缸套在3个工况下的径向变形和轴向变形，分析了缸套在不同工况下的整体变形、轴向变形和径向变形，发现热载荷对缸套的变形起主要作用。在分析径向变形时，采用傅里叶变换的方法得到了缸套在装配工况下第2阶至第8阶的变形值。从结果来看，缸套变形满足要求。

1李坤，苏铁熊，赵静．顶置湿式气缸套温度场及热机耦合分析[J]．小型内燃机与摩托车，2010（2）：45-48．

2张运泉，沈捷，杨剑等．有限元分析柴油机气缸孔变形的研究[J]．内燃机，2009（5）：14-17．

3夏春晶，刘玉凤，闫明等．气缸盖蠕变－疲劳寿命预测[J]．失效分析与预防[J]，2008（1）：59-63．

4俞小莉，郑飞，严兆大等．内燃机气缸体内表面稳态传热边界条件的研究[J].内燃机学报，1987（4）：329-332．

5周舟，杨怀刚．发动机气缸盖气缸体一体化三维模拟研究[J]．车用发动机，2007（5）：56-58．

6陈亮，路明．基于有限元的缸孔变形量分析[J]．汽车工程师，2012（6）：49-51．

Deformation Analysis of the Cylinder Liner based on Mechanical-thermal Coupling

Zhu Xiaoping,Bai Shu,Chen Yang,Song Hongnian
（Shanghai Diesel Engine Co.,Ltd.,Shanghai 200438,China）

The t emperature f ield of the cylinder liner was analyzed via the mechanical-thermal coupling method.The coupling field based on the thermal analyzing results was calculated.The influence of the different load on the deformation was analyzed.The calculated results indicated that the maximum temperature of the cylinder liner was 230.6℃,which appeared on the upper part of the inner face in the cylinder liner.Over all,the deformation of the cylinder liner satisfied the requirement.The thermal load was the most important factor to the deformation of the cylinder liner.The results were very useful for the design of the cylinder liner.

cylinder liner,temperature field,coupling field,deformation

10.3969/j.issn.1671-0614.2013.03.003

来稿日期：2013-05-16

朱小平（1987-）男，CAE工程师，主要研究方向为发动机结构疲劳可靠性。