基于非线性动态逆的水下运载器控制方法研究

崔乃刚，白瑜亮，常亚武，王小刚，许江涛

(1.哈尔滨工业大学 航天学院，黑龙江 哈尔滨150001;2.哈尔滨工程大学 航天学院，黑龙江 哈尔滨150001)

0 引言

传统的控制器设计在处理非线性系统时，通常是将过程模型线性化，然后再利用线性系统控制理论设计相应的控制器[1]。在很多公开发表的文献中利用状态反馈控制、LQR 方法[2－4]、切换控制方法、双模态方法、反馈线性化方法、LQG 方法、PID 控制[5－6]及滑模变结构控制方法设计了相应的控制器。这些方法均是利用小扰动理论在水下运载器非线性模型的某一平衡位置进行泰勒展开，进而得到近似的线性模型，而后对其进行控制器设计。然而，这些方法用于非线性系统并不总能得到理想的结果。尤其在水下运载器姿态控制问题中，由于系统的高度非线性、强耦合及姿态变化较大，问题更加严重，其主要原因是在线性化过程中将不可忽视的非线性关系用线性关系代替或忽略了。

对于如何解决水下运载器非线性控制以及存在不确定性和外界干扰作用时的运动稳定性问题，国内外已有学者进行了研究。文献[7]结合模糊控制原理与PID 控制应用形式设计了一种S 控制器，结合WL－2 实验数据通过仿真验证了S 控制器的性能。Vuilme[8]设计了一种带有加速度反馈的MIMO Backstepping 控制器，通过数值模拟验证了在存在洋流干扰和参数不确定性情况下，控制器具有鲁棒性。文献[9]根据滑模控制理论，设计了一种鲁棒跟踪控制器。仿真结果表明该控制器具有良好的鲁棒性，对参数变化和干扰存在情况下具有良好的跟踪性能。张浩[10]在水下运载器纵向运动模型的基础上设计了俯仰角、偏航角以及深度的PID 控制器，并采用遗传算法对控制器参数进行整定，同时为了解决控制对模型的依赖设计了模糊控制器，取得了较好的效果。但其PID 控制器是在简化模型基础上设计而来，对于非线性考虑不够;而模糊控制器虽然解决了对模型的依赖，但其控制精度受到影响。张晶晶[11]针对五自由度水下运载器动力学模型的参数不确定性设计了一种鲁棒自适应控制器，其不需要已知精确模型参数，就可以获得较好的系统稳定性，解决了系统不确定性问题，但其忽略了水下运载器动力学模型中滚转通道的耦合影响，具有一定的局限性。

尽管上述研究对水下运载器非线性控制以及动力学模型存在不确定性和外界干扰问题已有一定的研究成果，然而研究还不够深入，针对性并不是很强，无法体现控制对象(水下运载器)的特殊性。因此，必须寻找新的非线性控制方法，设计新的控制器。

非线性动态逆方法理论上形式统一、物理概念上清晰直观、使用上简单明了[12]，能够适应水下运载器非线性强耦合的控制要求。以时间为尺度将系统划分成慢变的角度动力学和快变的角速度动力学，然后对各个回路分别进行设计，通过划分快、慢子系统，可实现将全系统的控制器设计问题转换为子系统的控制器设计问题，计算的复杂性也得以降低，但该方法只能用于系统变量在时间尺度上有明显差别的系统[13－14]。

本文从水下运载器动力学模型建立出发，基于非线性动态逆控制理论，将系统划分为慢回路和快回路，通过状态反馈分别设计了慢回路姿态控制器和快回路姿态控制器，解决了非线性、强耦合的控制问题;然后通过Lyapunov 稳定性分析证明了控制系统的稳定性。最终非线性仿真验证了控制系统的有效性。

1 水下运载器运动数学模型

考虑非线性动态逆控制的需要，建立水下运载器非线性运动数学模型。

运载器体坐标系Oxbybzb:原点位于运载器质心处，Oxb轴沿运载器纵轴指向前方;Oyb轴在纵对称面内垂直于Oxb轴，向上为正;Ozb轴与Oxb轴、Oyb轴构成右手系。

设水下运载器的角速度ω 及质心处的速度v 在水下运载器体坐标系中的3 个分量分别为ωx、ωy、ωz，vx、vy、vz;水下运载器的质量为m，水下运载器Oxb轴、Oyb轴、Ozb轴的3 个转动惯量分别为Jx、Jy、

水下运载器的动量Q 和动量矩K 在水下运载器体坐标系中的3 个分量可以表示为

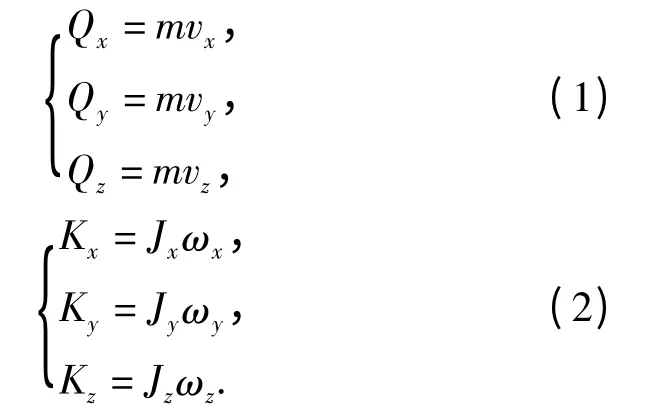
将(1)式、(2)式代入普遍使用的刚体动量和动量矩方程

式中:F、M 为作用在水下运载器上的所有外力的合力与合外力矩，包括重力和浮力、流体动力及其力矩;ω 为水下运载器体坐标系绕惯性坐标系的旋转角速度矢量。

将附加质量的表达式引入方程的左边，经运算、展开及整理，则动力学方程可写成矩阵的形式

式中:(Fx，Fy，Fz)为作用在水下运载器上的所有合外力F 在水下运载器体坐标系下的3 个分量;(Mx，My，Mz)为合外力矩M 在水下运载器体坐标系下的3 个分量;λ11，λ22，λ33为运载器的附加质量;λ44，λ55，λ66，λ26，λ35为运载器的附加转动惯量。

为了避免大俯仰情况下出现奇异，水下运载器体坐标系到地面坐标系之间的转换顺序为Z(θ)→Y(ψ)→X(φ).水下运载器旋转角速度与3 个姿态角变化率之间的关系式采用如下方程表示:

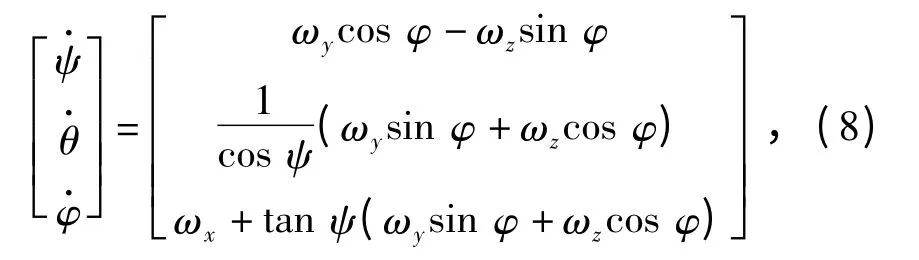
式中:ψ、θ、φ 为水下运载器的偏航角、俯仰角和滚转角。

2 动态逆控制器设计及稳定性分析

对水下运载器运动过程的控制，主要是控制姿态角和角速度，以满足期望俯仰角θ、偏航角ψ、滚转角φ 的要求。

根据状态变量动态响应过程的时间尺度差异采用层叠结构控制的思想，选取如下两组变量:快变量ωx，ωy，ωz，慢变量θ，ψ，φ.由水下运载器航行力学可知，控制系统对于θ，ψ，φ 的作用是比较慢的，对于ωx，ωy，ωz的作用则很快，因此在求解ωx，ωy，ωz子系统的动态逆时可认为θ，ψ，φ 是常量。首先以指令姿态角与实际姿态角的偏差作为输入，通过慢回路姿态控制器得到期望角速度;其次以期望角速度与实际角速度的偏差作为输入，经过快回路姿态控制器得到指令舵偏;最后，指令舵偏输入非线性模型进行弹道解算。设计快回路带宽为慢回路带宽的5 ～10 倍，这样可以使得快回路快速精确地跟踪慢回路[13]。系统框图如图1 所示。

图1 非线性动态逆控制结构示意图Fig.1 Nonlinear dynamic inversion control structure diagram

根据非线性动态逆控制器设计的需要，此处忽略浮力造成的力矩对水下运载器的影响，可以通过制导环节进行补偿。由前文所述水下运载器运动模型可以得到慢回路和快回路运动方程。

记

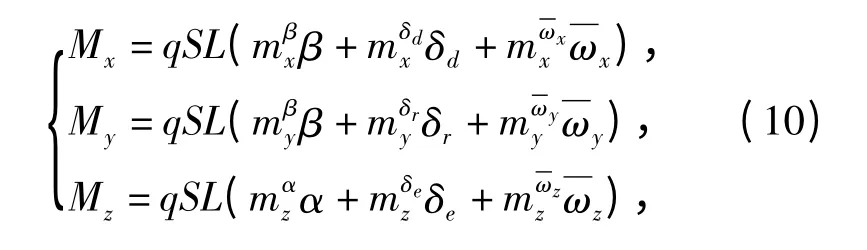
则有

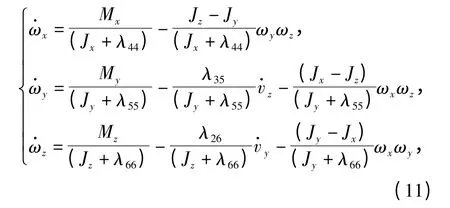
式中:Mx，My，Mz为作用在运载器上的除去浮力造成的力矩以外的总力矩在本体坐标系3 个轴的投影;为水动力矩系数;α，β，q，S 和L 为攻角、侧滑角、动压、特征面积和特征长度。

2.1 慢回路动态逆控制器设计

慢回路动态逆控制器根据由制导系统产生指令要求θc，ψc，φc以及水下运载器自身状态变量，设计出合理的角速度指令ωxc，ωyc，ωzc，并输出到快回路中。

首先证明慢回路动态逆控制器的稳定性。由方程可以得到水下运载器的慢回路运动模型。

式中:xf=[ωx，ωy，ωz]T;xs=[θ，ψ，φ]T;

令xsc=[θc，ψc，φc]，定义跟踪误差

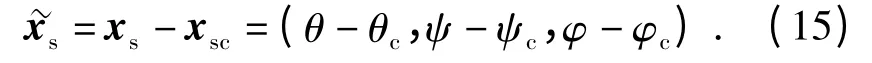
取慢回路输出为(θ，ψ，φ)，又因gs(xs)可逆，对(18)式进行反馈线性化，可得控制律如下

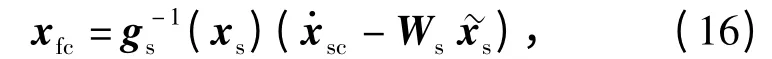
式中:Ws=diag(Wθ，Wψ，Wφ)，Wθ，Wψ，Wφ均大于0.

将(16)式代入(12)式可得系统闭环状态方程

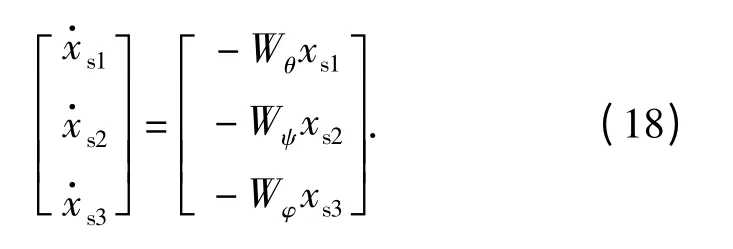
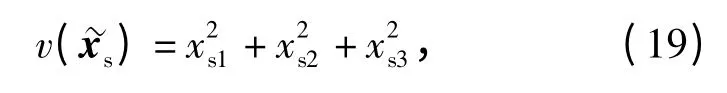
则有

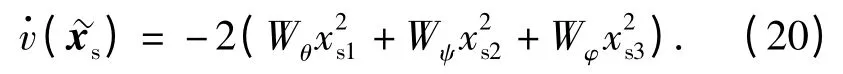
由于Wθ，Wψ，Wφ均大于0，显见)为负定。又由于→∞时)→∞，)为负定不变，故慢回路系统在式控制律条件下为大范围渐进稳定。

2.2 快回路动态逆控制器设计

快回路动态逆控制器根据慢回路动态逆控制器产生的角度指令ωxc，ωyc，ωzc，以及水下运载器自身的状态变量，获得舵偏指令δec，δrc，δdc，最终作为控制模块的输入。

由方程可以得到水下运载器的快回路动力学模型

式中:

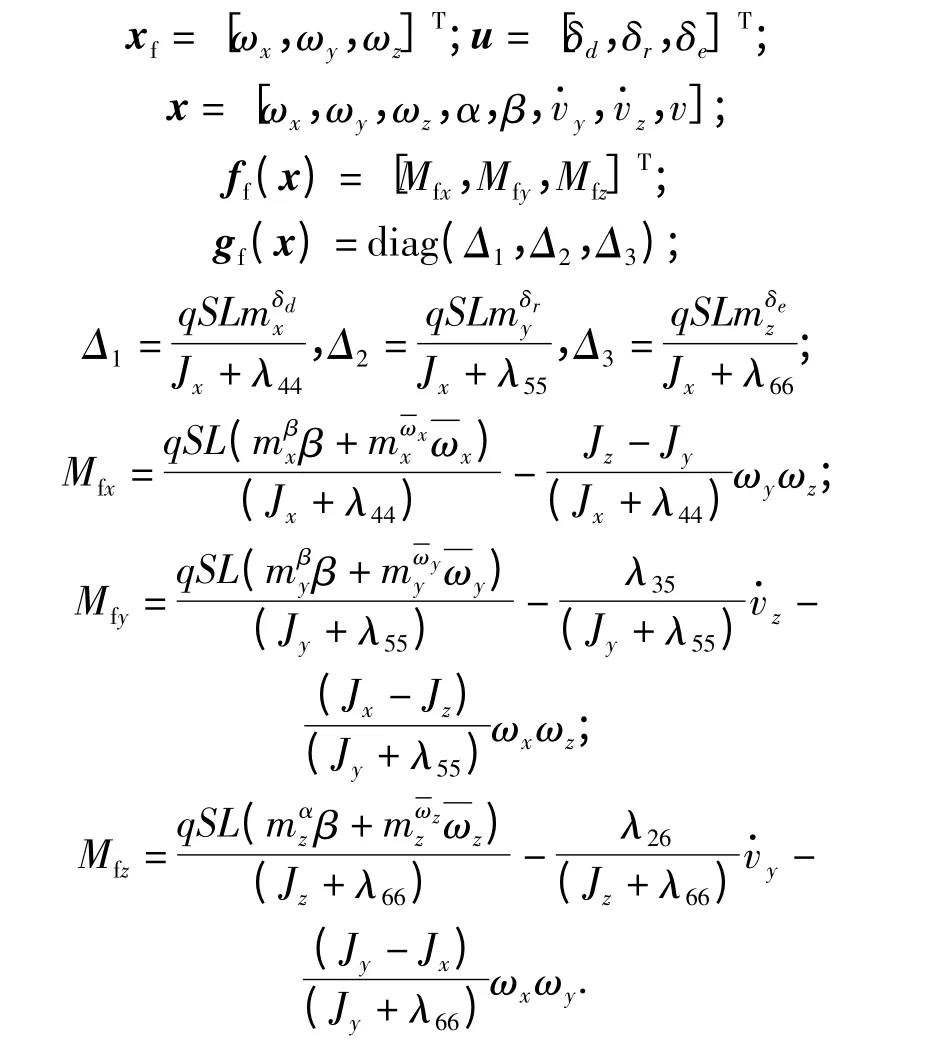
当Δ1Δ2Δ3≠0 时，则gf(x)可逆。令xfc=[ωxc，ωyc，ωzc]T，定义跟踪误差

快回路输出为ωx，ωy，ωz，又因gf(x)可逆，对(22)式进行反馈线性化，可得控制律

将(23)式代入(21)式可得系统闭环状态方程

快回路稳定性证明过程与慢回路证明过程类似。

3 计算结果与比较

在MTLAB/SIMULINK 环境下建立水下运载器非线性运动数学模型，并考虑实际舵机转角限制。在设计控制器时，快回路带宽是慢回路带宽的5 ～10 倍，使得快回路精确地跟踪慢回路。取参数Wωx=Wωy=Wωz=10 s－1，Wθ=Wψ=Wφ=2 s－1.以标准俯仰角，偏航角和滚转角作为控制系统的指令信号，验证所设计的控制器。初始条件:x = z =0 m，y= －40 m，α=β=φ=0°，v=10 m/s，M=1 840 kg，ψc=φc=0°.

实际舵机转角限制为±20°.俯仰角指令信号θc如图2 所示。

为了比较非线性动态逆控制器(简称DI 控制器)与PID 控制器之间的动态性能，通过跟踪单位阶跃信号，分析二者在动态性能方面的差别。

图2 俯仰角指令信号Fig.2 Pitch angle command signal

通过图3 可知，DI 控制器超调量为4%，稳态时间为1 s，稳态误差为零;而PID 控制器超调量为12%，稳态时间为1.5 s，稳态误差为0.2%.由此可知，DI 控制器实现控制需要时所需的控制力矩较小，能够实现快速跟踪，跟踪精度高，体现了其精确线性化的能力。

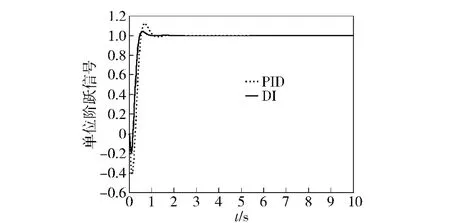
图3 跟踪单位阶跃信号对比图Fig.3 Chart of tracking unit step signal

为了进一步分析DI 控制器的性能，在不考虑水动力参数不确定性和考虑水动力参数不确定两种情况下进行非线性仿真，将DI 控制器俯仰通道仿真结果与PID 控制仿真结果进行对比分析。下面给出PID 控制器三通道控制参数:

俯仰通道比例系数Kfp= 0.347 5;积分系数Kfi=6.513 9;微分系数Kfd= －0.039 1.

偏航通道比例系数Kpp= －0.2;积分系数Kpi=9.580 1;微分系数Kpd=0.043 2.

滚转通道比例系数Kgp=0.171;积分系数Kgi=0.006;微分系数Kgd=0.435.

在水动力参数无不确定性时，与PID 控制器俯仰通道仿真结果对比如图4 所示，图5 给出了DI 控制器的偏航角和滚转角跟踪误差，图6 给出了DI 实现跟踪所需的舵偏。在水动力参数－30%不确定性时，DI 控制器与PID 控制器俯仰通道仿真结果对比如图7 所示。图8 给出了DI 控制器的偏航角和滚转角跟踪误差，图9 给出了实现跟踪控制所需的舵偏。在水动力参数具有+30%不确定性时，DI 控制器与PID 控制器俯仰通道仿真结果对比如图10 所示。

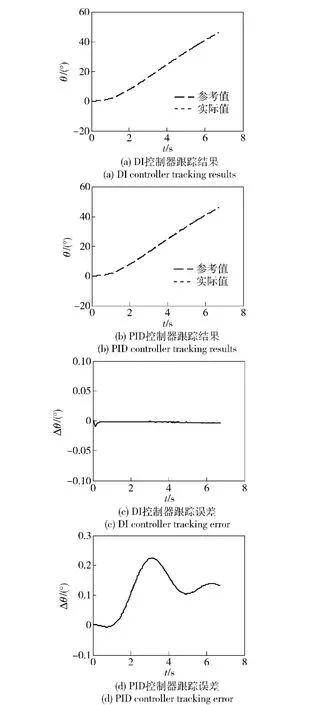
图4 无不确定性俯仰角对比Fig.4 Tracking pitch angle with uncertainty

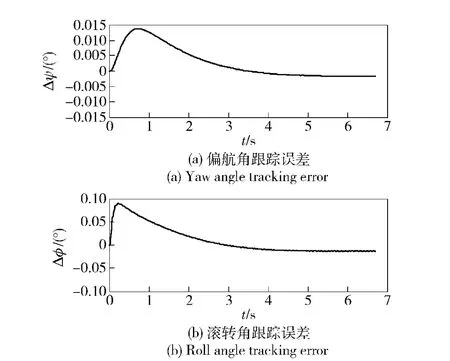
图5 无不确定性DI 控制器偏航角及滚转角跟踪误差Fig.5 Tracking error of yaw angle and roll angle for DI controller with uncertainty

图6 无不确定性指令舵偏Fig.6 Rudder Instructions with uncertainty

通过仿真可以看出，在不考虑水动力参数偏差时，DI 控制器与PID 控制器都能够很好地跟踪指令信号，但是由跟踪误差可以看出DI 控制器跟踪误差更小。当水动力系数有30% 偏差时，PID控制跟踪误差明显变大且有发散的趋势，而DI 控制跟踪误差仍然很小。因此，DI 控制具有较好的跟踪性能，能够精确地跟踪指令信号，同时具有一定的鲁棒性。

4 结论

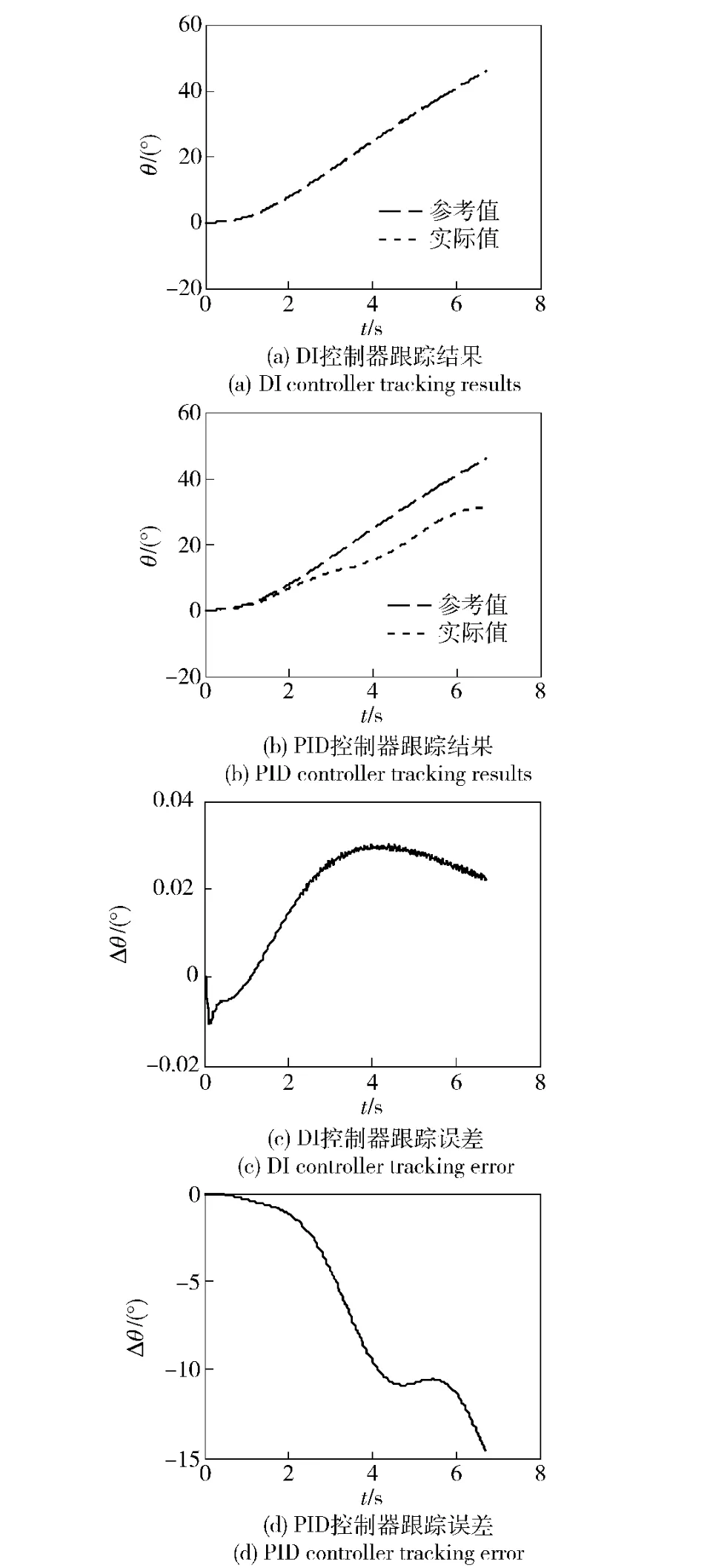
图7 －30%不确定性俯仰角对比Fig.7 Tracking pitch angle with －30% uncertainty

本文控制方法在动态特性方面较PID 控制方法具有较大提升，体现了非线性动态逆方法对非线性系统具有精确线性化的能力;在水动力参数存在不确定性情况下，本文控制器仍具有较好的跟踪性能，体现了该控制方法具有一定的鲁棒性;最重要的是本文控制器设计过程中不需要对动力学模型进行小扰动线性化，因此非常适用于非线性、强耦合、大攻角航行以及姿态变化剧烈的水下运载器控制系统。但是，由于逆误差的存在，会对控制器的性能产生影响，当逆误差很大时控制器甚至出现不稳定。后续考虑引入鲁棒控制方法对本文控制器进行改进，以保证在逆误差存在的情况下，控制器仍能使系统满足鲁棒性要求，进一步提高水下运载器的控制品质。

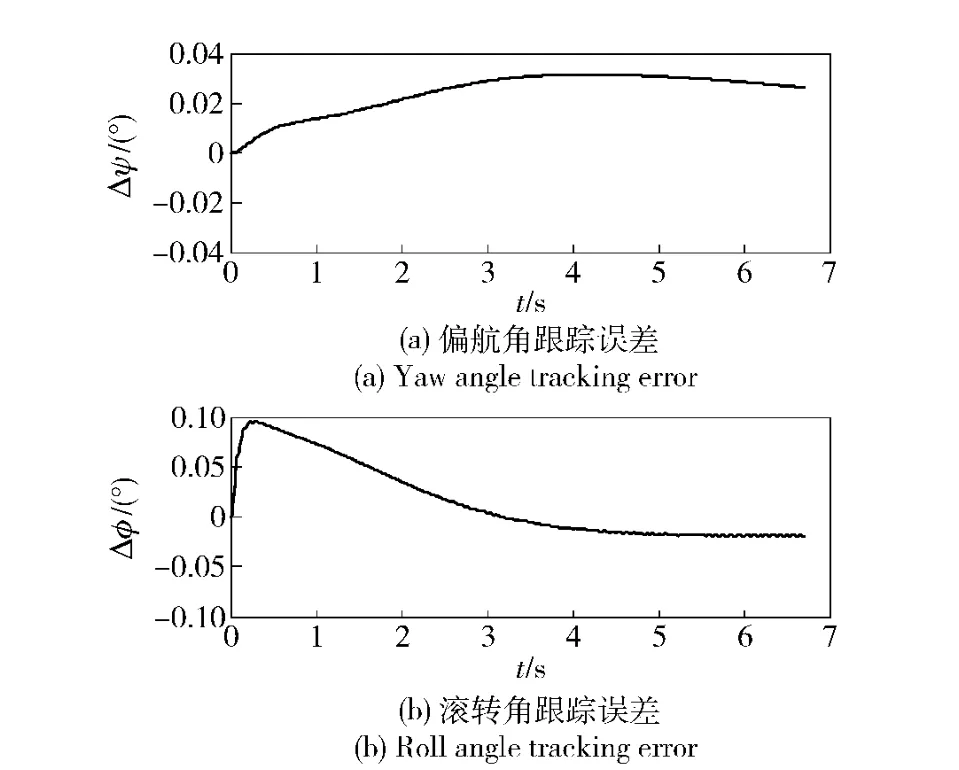
图8 －30%不确定性DI 控制器偏航角及滚转角跟踪误差Fig.8 Tracking error of yaw angle and roll angle for DI controller with －30% uncertainty

图9 －30%不确定性指令舵偏Fig.9 Rudder Instructions with －30% uncertainty

图10 30%不确定性俯仰角对比Fig.10 Tracking pitch angle with 30% uncertainty

图11 30%不确定性DI 控制器偏航角及滚转角跟踪误差Fig.11 Tracking error of yaw angle and roll angle for DI controller with 30% uncertainty

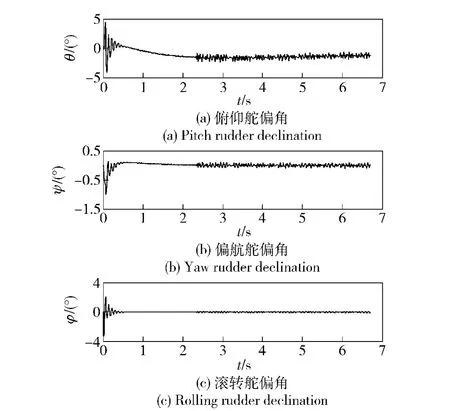
图12 30%不确定性指令舵偏Fig.12 Rudder Instructions with 30% uncertainty

References)

[1]李怡勇，沈怀荣.无人机非线性动态逆控制器的设计研究[J].航天控制，2007，25(5):54 －57.LI Yi－yong，SHEN Huai－rong.Gain－scheduling design of UAV flight controller[J].Aerospace Control，2007，25(5):54 －57.(in Chinese)

[2]Leonard N E，Graver J G.MODEL－based feedback control of autonomous underwater gliders[J].IEEE Journal of Oceanic Engineering，2001，26(10):633 －645.

[3]Lei K，Zhang Y，Fan H，et al.Matlab－based simulation of buoyancy－driven underwater glider motion[J].Journal of Ocean University of China，2008，7(2):113 －118.

[4]Wang Y，Zhang H，Wang S.Trajectory control strategies for the underwater glider[C]∥International Conference on Measuring Technology and Mechatronics Automation，2009.ICMTMA'09.IEEE，2009，1:918 －921.

[5]Bachmayer R，Graver J G，Leonard N E.Glider control:a close look into the current glider controller structure and future developments[C]∥Proceedings of OCEANS 2003.San Diego，CA:IEEE，2003:951 －954.

[6]Seo D C，Jo G，Choi H S.Pitching control simulations of an underwater glider using CFD analysis[C]∥Proceedings of OCEANS 2008.Kobe:IEEE，2008:1 －5.

[7]Wang B，Su Y，Wan L，et al.Modeling and motion control system research of a mini underwater vehicle[C]∥International Conference on Mechatronics and Automation，2009.ICMA 2009.IEEE，2009:4463 －4467.

[8]Vuilmet C.A MIMO backstepping control with acceleration feedback for torpedo[C]∥Proceedings of the 38th Southeastern Symposium on System Theory.Cookeville:IEEE，2006:157 －162.

[9]Yang H，Ma J.Sliding mode tracking control of an autonomous underwater glider[C]∥2010 International Conference on Computer Application and System Modeling.Taiyuan:IEEE，2010:555 －558.

[10]张浩.水下运载器参数辨识与控制方法研究[D].西安:西北工业大学，2006.ZHANG Hao.Parameter identification and control methods of underwater vehicles[D].Xi'an:Northwestern Polytechnical University，2006.(in Chinese)

[11]张晶晶.基于远程遥操作的水下运载器的控制器设计[D].上海:上海交通大学，2011.ZHANG Jing－jing.Control design of remotely operated vehicles based on teleoperation[D].Shanghai:Shanghai Jiaotong University，2011.(in Chinese)

[12]李春文，冯元琨.多变量非线性控制的逆系统方法[M].北京:清华大学出版社，1991.LI Chun－wen，FENG Yuan－kun.Multivariable nonlinear inverse system control method[M].Beijing:Tsinghua University Press，1991.(in Chinese)

[13]雷延花，陈士橹.非线性动态逆在大攻角导弹控制系统设计中的应用[J].弹箭与制导学报，2002，23(1):109 －112.LEI Yan－hua，CHEN Shi－lu.Nonlinear dynamic inversion applied to design of control system for high angle of attack missile[J].Journal of Projectiles，Rockets，Missiles and Guidance.2002，23(1):109 －112.(in Chinese)

[14]Wise K.Nonlinear aircraft flight control using dynamic inversion[C]∥Proceedings of the 11th American Control Conference.Chicago:IEEE，1992:1322 －1326.