桅杆型光电探测系统总体精度分析

陈兆兵，王兵，陈宁，时魁，刘长顺

(中国科学院 长春光学精密机械与物理研究所，吉林长春130033)

0 引言

随着光电探测系统在小型化、多功能、高成像质量等方面的要求越来越高，各种光电探测系统在经过加工和装调后其探测成像质量与初始设计指标相差很大，甚至连预定的使用要求都无法满足。如果得不到各项精度误差对探测成像质量的影响定量数据，就无法在系统设计、加工、装调及使用时对系统误差进行有针对性的修正。因此从光电探测系统的工程应用前景来看，为此类系统建立合理完善的误差分配体系是必不可少的，对该类系统进行必要的精度分析也是光电探测系统工程化应用的必要条件之一。

目前国内外针对光电探测系统本身的精度分析与误差分配的研究较为深入。很多光电探测系统在加工之前都建立了以精度分析为基础的误差分配体系。如美国的4 m 大口径光电探测系统在设计之初就通过精度分析进行了多种方案的误差分配，为系统的加工、装调与使用提供了理论参考[1]。将光电探测系统架设于桅杆顶端进行应用在国外是近几年才出现。若采用传统的光电探测系统精度分析方法对本文所探讨的系统进行分析则无法体现作为承载平台的光电桅杆的自身误差对系统探测成像质量的影响。因此有必要在此类系统工程化应用之前建立一套合理有效的精度分析与误差分配方案指导系统的应用。

本文为解决传统车载式光电探测系统易受地形遮挡无法远距离探测的问题，提出一种车载桅杆高架式光电探测系统，对该系统进行整体的精度分析与误差分配。并对光电探测系统本身及桅杆承载平台在方位方向进行了整体精度分析。在研究中引入对光电桅杆自身精度分配与分析的策略。依据总体精度指标及系统参数分配了各项误差并采用计算与试验的方式验证了误差分配的合理性，从而为此类桅杆平台型光电探测系统的精度分析与误差分配体系的建立提供了理论参考。

1 系统精度指标与误差分配的组成

桅杆型光电探测系统的一个重要组成部分是作为支撑结构的桅杆，桅杆的精度与稳定性在很大程度上将会影响系统的整体精度。为了简化模型，在整体误差计算中，将桅杆平台的误差作为一个整体因素进行探讨，专门针对桅杆的误差分配与计算验证进行探讨。在分析中不考虑承载光电桅杆的载车的振动，将桅杆底部看成与地面成刚体状态。根据光电探测系统的作用距离、探测目标类型、系统本身的参数水平及目标引导精度要求确定的桅杆型光电探测系统在方位方向的总体精度指标值为25″.将此总精度值分配给光电探测系统本身和桅杆系统，分别根据其自身参数计算是否满足分配指标。通过试验验证该分配是否合理。对光电探测系统的分析需要充分考虑误差的种类、来源、性质与传递规律，同时根据光电系统的总精度要求和可靠性要求，对组成系统的各个零部件的误差进行合理的分配及可靠性设计与分析预测，从而确定光电系统各零部件的制造与装调技术要求，使系统的精度满足要求，并在系统加工、装调与使用过程中进行合理的误差控制。根据系统中误差的种类、来源及性质等的不同，将桅杆型光电探测系统分为4 部分:1)轴角编码器(采用光电式轴角编码器，这种测角系统由光学系统、精密机械系统、电子系统组成);2)瞄准系统(采用内调焦式红外系统);3)转轴系统(采用两轴结构，分别为方位轴和俯仰轴);4)平台系统(为光电系统提供安装与运行平台，包括组成桅杆的各段机械结构、调平系统)。

桅杆型光电探测系统除了探测系统自身的误差外，还受到风载、车辆振动等随机误差的影响，因此需要对随机误差进行合理分配，在这个过程中往往采用等作用分配原则或加权作用原则。这种方法将设备的各个环节及各个零部件的源误差对光电设备总体的误差影响是大小一致的[2－3]。而加权作用原则需要在考虑设备各个环节的局部误差对系统总体的误差存在影响程度不一致外还要考虑设备的不同环境对整体的误差控制存在控制难易程度不一致的情况[4]。这种分配方法比较接近实际的情况，在本文的研究中将采用这种方法。

2 系统总体精度的计算与分析

2.1 桅杆型光电探测系统总体精度计算

光电系统参数:

1)方位轴角编码器:直径120 mm，最小读数2″.

2)俯仰轴角编码器:直径100 mm，最小读数2″.

3)瞄准系统:红外系统放大倍率Γ=30，最短视距500 m.

4)方位轴系统:轴内径100 mm，外径450 mm，轴承滚珠直径5 mm，高度150 mm，轴隙Δd =0.003 mm.

5)俯仰轴系统:外径15 mm，轴承滚珠直径5 mm，轴隙Δd=0.003 mm.

6)读数系统:采用红外CCD，以液晶显示为主读数方式。

7)安装平台系统:5 节5 m 式升降式桅杆平台结构，4 组连接配合组件。

桅杆型光电探测系统的主要误差是方位方向的扭转误差，该误差更能影响以远距离探测为目的光电探测系统的跟踪精度，因此在误差分析上将以方位方向的误差为研究重点。首先对系统的误差来源进行探讨，设备的误差主要由人为误差、外界误差、设备误差三项组成。其中人为误差是由于设备操作人员在熟练程度、疲劳程度、心理状态不一造成的，在不同的情况下读数误差的大小是不一致的。外界误差则既包括温度气候、大气吸收折射等纯外部因素，又包括探测系统的支撑安装平台—桅杆的稳定性因素[5]。在参考同类型的光电设备室内外测量的平均值，同时充分考虑高架桅杆受风载振动的平均值后，取这项因素的误差标准差为光电系统安装误差值与桅杆作用到平台上的误差值之和，可表示为σo=σin+σm，σo为外界误差，σin为安装误差，按经验可取为5″，σm为桅杆作用到平台上的误差，根据经验光电探测系统的本身误差值一般为0.7″ ～2.8″，取光电设备本身的分配许用误差值为Δσs=2″.光电设备本身的误差包括轴角编码器误差σc，光电系统瞄准误差σa，系统整体的轴系误差σts，人眼判读误差σr等几项，下面分别对各项误差值进行计算与分析。

由光电系统的误差来源可得综合(1)式，误差的分配也可以采用(1)式进行:

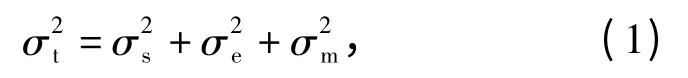
式中:σt为总误差;σs为光电设备本身的分配误差;σe为人眼判读误差。

为简化模型假设许用人眼判读误差Δσe=6.7″，又知许用总体误差Δσt=25″，Δσs=2″，代入(1)式，即可求得光电设备本身的误差值与桅杆带来的误差值:

从(2)式可以看出，分配给光电桅杆的误差为主要误差源。

2.2 光电探测系统本身的精度分析

光电探测系统的原始误差有20 多项，文献[6]将此类系统的误差分配中光电设备本身的误差归结为六项。此处将光电探测设备的安装误差归结到桅杆平台的误差中进行分析。由于将影响较大的桅杆及安装平台误差剥离出了光电设备的本身总误差，因此可以按等精度原则对光电设备本身的分项误差进行分析，如(3)式所示。

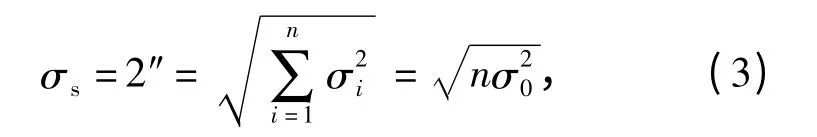
式中:σi为各分项误差;σ0为各分项误差的平均值，通过该值可以反向推得光电探测系统各分项的原始误差允许值。但由于光电探测系统本身的误差因素非常复杂，各单项精度上的计算结果并不精确，因此有必要通过对系统各单向原始误差分别进行误差计算的方式得到综合误差。

伺服系统中的光电编码器的最大误差可以取为1″，此项误差服从均匀分布，其分布系数可以取为光电轴角编码器误差值为

由误差理论和仪器精度理论知，光电系统的对准误差和瞄准误差的视差量分别为

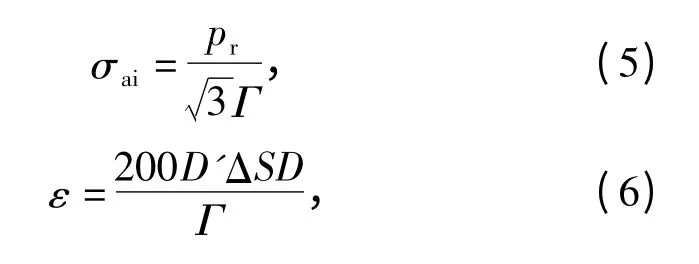
系统轴系误差包括方位轴误差和俯仰轴误差，由于间隙的存在方位轴存在一定的角度晃动，该轴运行过程中偏离铅垂线的最大晃动角为

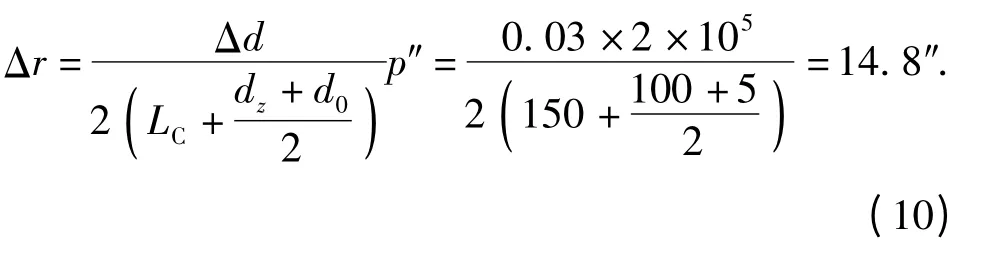
在方位轴系误差的计算中假设目标的垂直角为±6°，又由于该误差可以认为是服从均匀分布，因此方位轴系误差为

式中:方位轴系误差σpa为轴系总误差σts的一部分，由于本文仅探讨系统的方位误差，因此未计算轴系总误差σts.

俯仰轴误差为轴系误差的一个重要方面，该误差对方位误差也存在一定的影响[7]。俯仰轴横跨在光电探测系统结构的左右轴承之间，该轴的误差主要是由于两轴承高度不一致、俯仰轴存在装配间隙以及轴颈的椭圆度存在误差等因素造成。前两项误差可以采用正倒镜测量法及Ⅴ形轴系结构消除，在俯仰轴的误差上仅需要对椭圆度误差进行重点考虑，当俯仰轴两端椭圆的长轴互成直角时，该轴处于最大的倾斜角为

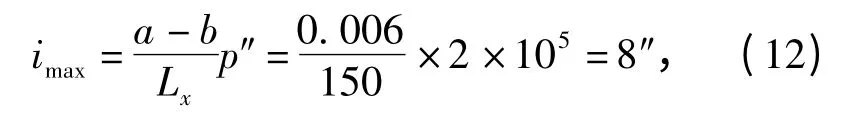
式中:a－b 为椭圆度，可取值为0.006 mm;Lx为俯仰轴的跨度，其值为150 mm.

俯仰轴的误差可以近似由测角误差代替，测角误差服从均匀分布，可用(13)式表示。轴系误差则可由(14)式表示。

在进行角度读数及分析时采用数显方式，其误差最大值为其单个量化单位0.1″，又由于此误差可以认为是服从均匀误差，读数误差为

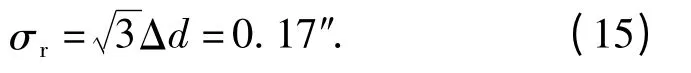
利用上述光电系统本身的分项误差值可以得到设备的总体误差，光电系统合成误差公式为

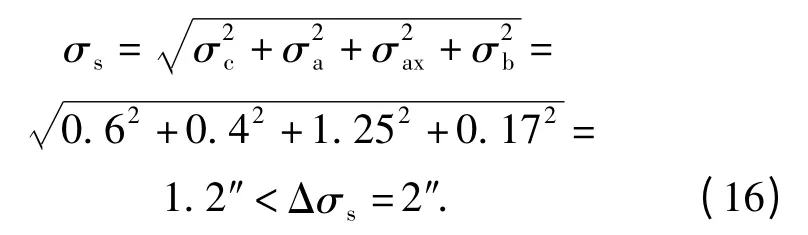
从(16)式中可以看出该合成误差小于分配的许用误差。

2.3 光电桅杆方位扭转精度分析

桅杆型光电探测系统的精度分配中桅杆本身的精度指标值为24″，因此根据桅杆及其附件的参数所计算得到的误差值需小于24″.本文探讨的是总体方位精度，当桅杆升起后与地面呈一定角度时，风载尤其是有扭转力的风载会在一定程度上造成桅杆的扭转，但这种扭转在中等风力条件下并不明显，且当桅杆处于与水平面垂直的稳定状态时风载并不会造成桅杆的直接扭转，因此桅杆在俯仰方向的晃动并不考虑。为了简化，假设桅杆工作时为5 节全部展开状态，同时桅杆与水平面呈垂直状态。在计算中引入电子水平仪的灵敏度误差σse、水平仪的调整误差σoe、桅杆整体的位移误差σme、光电探测系统安装偏心误差σge、光电探测系统步进控制带来的冲击误差σce、桅杆自身在方位方向的扭转误差σte等几项。桅杆由5 节机械结构嵌套而成，其周向扭转的最大间隙的合成为18″(即在风载作用为极限状态时桅杆的最大总扭转误差)，电子水平仪采用高精度装置，其数值直接传递给动态调平系统维持平台的水平稳定，光电探测系统对桅杆造成的冲击误差由于没有相近的经验数据参考，暂时以其最大加速度时对系统造成的扭转峰值作用为准，其值初步计算为8.6″，其他误差值以当前光电设备中普遍能够达到的精度标准的平均值为准，由(17)式可以求得桅杆的总体误差，该误差值小于分配的许用误差值。

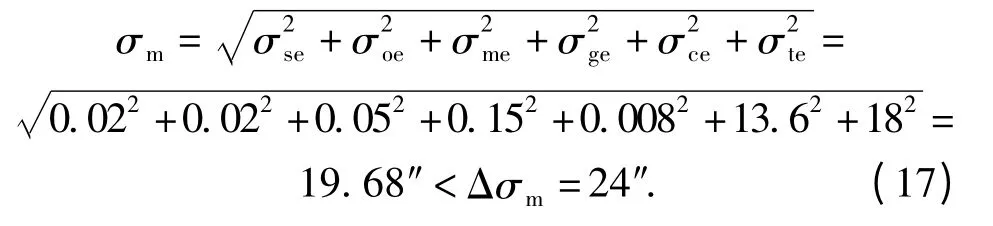
3 试验分析

为了对上述桅杆型光电探测系统精度的计算与分析有效性进行验证，对某试验型桅杆式光电探测系统的精度进行了试验测量。该试验采用国内某型车载光电探测系统与某型高精度光电桅杆，探测系统与桅杆的参数与上述计算中所取的参数一致。试验主要针对桅杆本身以及光电探测系统本身在方位方向的晃动误差进行验证。

3.1 固定方式

在试验状态下固定底段桅杆的架子可以看成是与地面成一体的，即认为桅杆的最底段是固定的，作用于桅杆上部的力对桅杆的底段是没有影响的。在这一前提下对桅杆在方位方向的精度进行验证才有意义。为了消除由于桅杆固定不稳造成光电探测系统的误差对桅杆系统进行了三重固定，分别为桅杆底部以大重量底板为固定件，将桅杆底座以螺栓的形式进行固定。桅杆第一节中用两个机械式抱环将桅杆固定在厂房的型钢柱子上，而第一节桅杆上部采用三组连杆将桅杆固定平台与地面连接在一起。通过三重固定，该桅杆与地面及厂房钢柱成为一个刚体。桅杆的固定如图1 所示。

3.2 检测方法

图1 桅杆的固定方式Fig.1 The fixation way of mast

将质量为100 kg 的光电探测系统架设到桅杆顶部的平台上，如图2 所示，图中左侧为光电桅杆及其支撑的光电探测系统，右侧为某便携式桅杆架设的平行光管，主要为光电探测系统提供稳定的目标源。为了全面衡量该桅杆在方位方向的间隙与扭转量，在试验过程通过多次升降多次测量与读数的方式得到总体误差值。具体方法为光电探测系统对距离为1 m 远的平行光管进行连续探测，由光电探测系统软件直接输出平行光源的偏差。同时为了剥离光电探测系统本身在方位方向的误差，采用将激光笔水平架设在桅杆顶端光电探测系统底端的方式测量桅杆本身在方位方向的偏差。当光电探测系统开机运行时打开激光笔，其光点将照射到距桅杆一定距离的靶板上，通过测量光点在方位方向的晃动量以及桅杆与靶面的水平距离便可以计算出桅杆本身的方位误差。将光电探测系统软件记录的总方位偏差减掉桅杆本身的误差便可以得到光电探测系统本身的误差。

3.3 试验

位于桅杆顶端的光电探测系统的连续旋转运动的运动速度为80 r/min.将桅杆型光电探测系统总体架设到光电桅杆顶部的平台上，将平行光管用另一根桅杆架设在桅杆型光电探测系统旁边，调整平行光管至桅杆型光电探测系统窗口等高位置，先手动调节光电探测系统窗口与平行光管光轴对齐并让光电探测系统窗口在静止状态下对平行光管目标进行扫描探测，然后桅杆型光电探测系统开始运动并对平行光管目标进行扫描。当桅杆型光电探测系统静止不动时，对目标的扫描值为目标的真实方位值;当桅杆型光电探测系统运动时，得到的目标扫描值为系统动态条件下光电桅杆与桅杆型光电探测系统作用下的探测方位值，对比两者的探测值，便可以得到桅杆型光电探测系统与桅杆系统总体的探测偏差值。所有取值均通过光电探测系统的软件直接输出，其探测数值以目标的能量中心为准。同时将激光笔稳定架设在桅杆顶端，记录系统运行时激光笔光点的运动量，计算得到桅杆在方位方向的精度值。

图2 试验系统图Fig.2 Testing system

3.4 试验结果与分析

通过对桅杆型光电探测系统总体的试验，得到结果如表1 所示。

表1 桅杆型光电探测系统方位精度试验结果Tab.1 The experimental results of mast－mounted photodetection system on azimuth direction

从表1 可知，上述针对某桅杆型光电探测系统在方位方向的精度分配基本上合理，无论是单项误差还是总体误差均与分配计算值相差不大，可以认为本文所探讨的这种桅杆与光电探测系统的精度同时探讨的方法是可行有效的。由于在试验过程中不考虑上述计算中的读数误差、水平仪误差及误差合成采用直接加减方式等因素，因此这种简化的试验与实际值将有一定的误差。

4 结论

针对桅杆型光电探测系统提出对该系统进行整体的桅杆系统与光电探测系统精度分析和误差分配的方案。将误差分配的结果用于桅杆型光电探测系统的加工、装调与使用过程。以某5 节型光电桅杆及其承载的光电探测系统为例，进行了精度分析，建立了一种以此型系统为对象的误差分配模式。通过理论计算与试验得到了系统在方位方向的误差值。研究结果表明，光电探测系统本身在方位方向的误差值远远小于桅杆系统在该方向的误差值，从整体上看本系统满足初始总误差分配要求。可以认为这种将光电探测系统与桅杆系统综合考虑进行精度分析与误差分配的方法是适用于此类高架式光电探测系统。桅杆型光电探测系统在俯仰方向的误差大小以及该误差对于方位方向误差的耦合作用如何等问题还需要做进一步研究。另外光电探测系统本身误差与光电桅杆承载平台误差之间的相互影响如何以及如何降低桅杆系统的误差对光电探测系统的最终成像质量影响将是今后研究的重点。

References)

[1]Hubbard R.ATST system error budge[J].ATST Project Documentation，2009.

[2]王志乾，赵继印，谢慕君，等.一种快速高精度自主式寻北仪设计及精度分析[J].兵工学报，2008，29(2):164 －168.WANG Zhi－qian，ZHAO Ji－yin，XIE Mu－jun，et al.Design and accuracy analysis for a fast high precision independence north －seeking[J].Acta Armamentarii，2008，29(2):164 －168.(in Chinese)

[3]玄伟佳，王东光，邓元勇，等.双折射滤光器的误差分析与性能优化[J].光学精密工程，2010，18 (1):52 －59.XUAN Wei－jia，WANG Dong－guang，DENG Yuan－yong，et al.Error analysis and performance optimization of birefringent filter[J].Optics and Precision Engineering，2010，18 (1):52 －59.(in Chinese)

[4]李婷，潘存云，李强，等.安装误差对球齿轮姿态调整机构指向精度的影响分析[J].兵工学报，2009，30(7):962 － 966.LI Ting，PAN Cun－yun，LI Qiang，et al.Analysis of assembly error affecting on directing precision of spherical gear attitude adjustment mechanism[J].Acta Armamentarii，2009，30(7):962 －966.(in Chinese)

[5]李俊峰，谢京江，宋淑梅，等.应用多模式组合加工技术修正大口径非球面环带误差[J].光学精密工程，2010，18 (7):1460 －1467.LI Jun－feng，XIE Jing－jiang，SONG Shu－mei，et al.Zonal error removal for large aspheric with multi－mode combined manufacture technique[J].Optics and Precision Engineering，2010，18(7):1460 －1467.(in Chinese)

[6]张福民，曲兴华，孟宪伟，等.一种机械寿命实验设计方法与精度分析[J].仪器仪表学报，2007，28(7):18 －24.ZHANG Fu－min，QU Xing－hua，MENG Xian－wei，et al.Design method for mechanical endurance test and its precision analysis[J].Chinese Journal of Scientific Instrument，2007，28(7):18－24.(in Chinese)

[7]叶鑫，张之敬，王强，等.微动工作台线性化精度评价方法研究[J].兵工学报，2008，29(6):741 －745.YE Xin，ZHANG Zhi－jing，WANG Qiang，et al.Research on linear accuracy evaluation method of a micro－manipulation platform[J].Acta Armamentarii，2008，29 (6):741 －745.(in Chinese)