运筹学中关于几类规划问题的教学研究

徐 鑫

（安徽大学数学科学学院，安徽 合肥 230601）

1 引言

在经典的运筹学教材中线性规划、目标规划以及多目标规划是分为三个独立的章节进行教学的，教材中所给出的例题也都是针对这三种规划问题按照各自章节介绍的方法进行优化和计算，如清华大学版运筹学教材[1]中第一章“线性规划及单纯形法”与第四章“目标规划”中涉及了许多应用的例子，有生产安排的、有合理利用材料的以及人员分配等例子；而文献[2-3]也仅仅对目标规划问题提出不同的优化方法；上述这些文献仅仅对所研究的规划问题进行研究，都没有从这三种规划的关系角度就探究它们的本质联系和区别，不具备一定灵活性、系统性；在教学过程中发现学生也只是机械的、单纯的会去了解这三种规划各自概念，然后按照书上给出的例题依葫芦画瓢地对相应的规划问题进行求解，学习过程很刻板，且学习之后也不能很好地将相关章节内容灵活地联系在一起，达到融会贯通；久而久之，学生不仅对所学内容理解不深刻，而且对相关章节联系的理解脱节，从而不易提升学生自己对学习新知的能动性、创造性和方法论。因为本文以文献[1]中例题为引例，结合多年教学过程的经验和心得来分析三种规划问题的联系，并得到有效的结论，为以后的教学创新提供绵薄之力。

2 可化为多目标规划问题的分析

2.1 线性规划（LP）与目标规划（LGP）的研究

2.1.1 引例

以[1]中P102例1为例，题为：某工厂生产Ⅰ、Ⅱ两种产品，已知有关数据见下表：

?

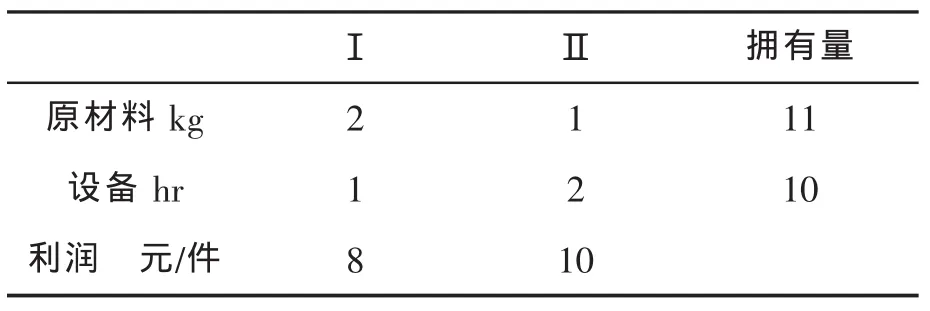
求获利最大的生产方案。

由例中讨论可用如下线性规划描述

其中X1，X2表示生产产品Ⅰ、Ⅱ的件数。

该工厂的目的是要在不超过所有资源限量的条件下，如何确定X1，X2以得到最大利润；所以上描述可转化为目标规划问题，其描述如下：

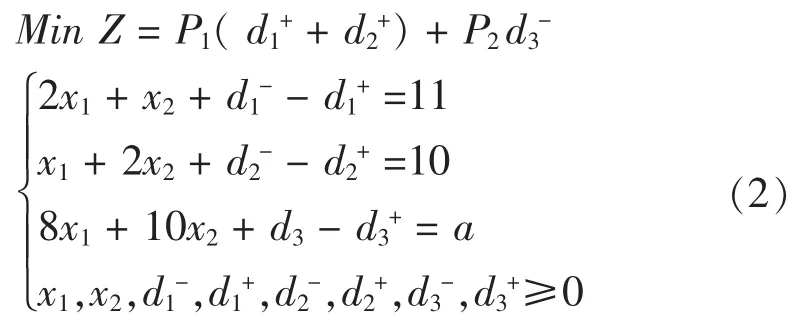
其中a为任一常数。

2.1.2 归纳及分析

我们通过上例得如下归纳：

对标准LP问题：

我们可以将（1）转化为LGP问题：

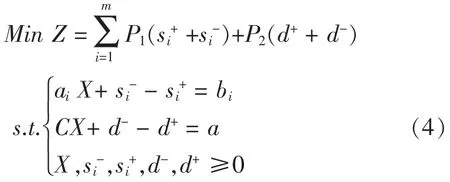
其中 a为任一常数 i=1，2，…，m

也就是说从LGP角度来看（4）式是除去一个目标外，把其余所有目标（在LP里的约束条件）放在等同的优先位置，要求它们必须尽可能地满足，在此前提条件下，把剩下的一个目标（在LP里称为目标函数）作为一级考虑因素予以最小化，显然对于（4）与（3）式并不等价，但作为 LGP模型，（4）叙述更为灵活。事实上LP问题（3）有可行解当且仅当问题（4）第一级目标值为零[4]，这时两问题的含义是相同的；若问题（3）无可行解，则（4）可以在其特定的算法中找到近似的可行点。

2.1.3 两种规划方法比较

一般来说LGP问题比LP问题更具有灵活性，也往往更切合实际。在应用型问题中，经常存在多个目标，这些目标之间可能冲突，可能相互联系，则此时满意解往往比最优解更具有现实意义。因为各目标优先级、同级中权系统以及指标值可由决策者提供。所以LGP与LP计算差别不大，同时LGP比LP更易求得结果。不过一旦数据改变，LGP问题也就随之改变，就得重新计算。

2.2 目标规划与多目标规划的研究

上述的引例在实际作决策的时候，要考虑到市场等一系列其它条件，如：引例的决策在原材料供应受严格限制的基础上考虑：首先是产品Ⅱ的产量不低于产品Ⅰ的产量；其次是充分利用设备有效台时，不加班；再次是利润不小于56元；求决策方案。

由分析可列得目标规划为：

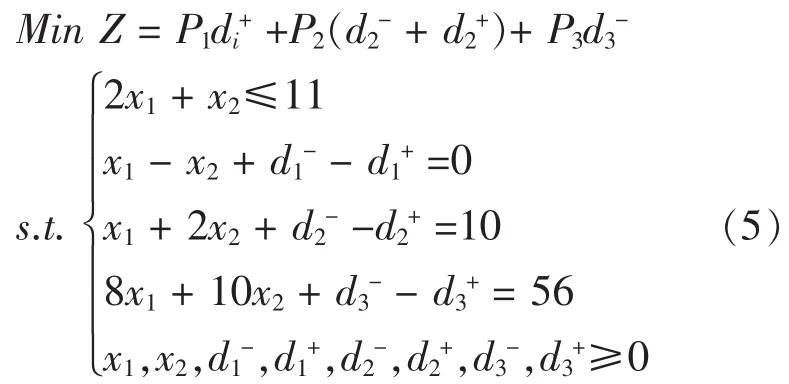
（5）中第一个条件是绝对约束条件，其余的是目标约束；（5）式可转化为多目标规划：

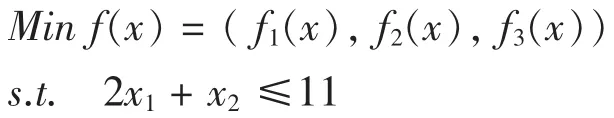
其中

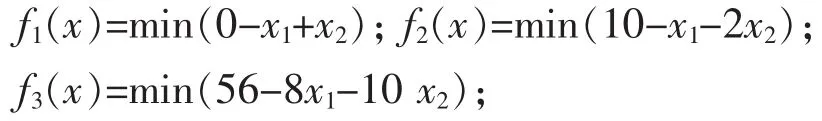
而目标规划中 P1，P2，P3相当于多目标规划中的权重，而权重是依实际情况由决策者而定；

我们可将上模型归纳为：

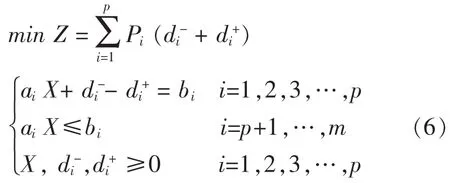
可将（6）式转化为：

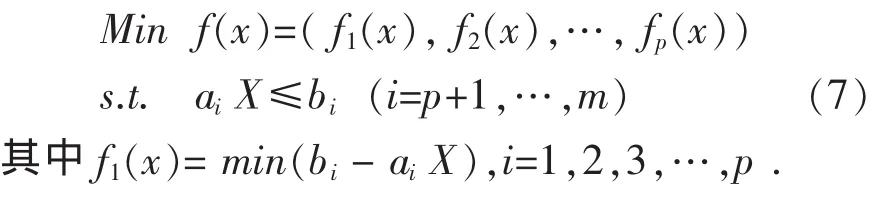
（7）中目标函数中的权重 ω=（ω1，ω2，…，ωm）是由实际因数加上决策者的偏好而定。

2.3 单目标规划与多目标规划的关系

线性规划是属于单目标规划问题，但单目标规划有其自身优点，在解决实际问题中也显出了其不足之处。在现实生活和实际工作中遇到更为普遍的问题常常含有多个目标，如生产问题中，又想使利润达到最大，又想使耗电量达到最小等。该问题只用有限个约束条件的单目标规划是解决不了的，就得依靠多目标规划进行求解，这就涉及到一个求解多目标规划问题。多目标解法很多，有TOPSIS法、夹角向量法、层次分析法等等[5]。但要找一种方法把单目标规划与多目标规划有机结合在一起的方法——加权和法，见如下定理：

定理 已知多目标决策问题：

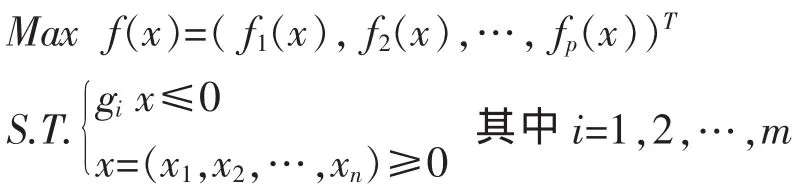
当各目标权重 ω=（ω1，ω2，…，ωp）＞0 时，下列单目标规划决策问题

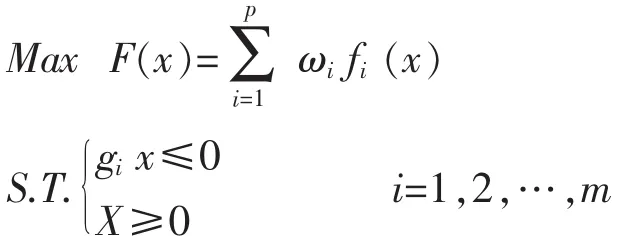
的最优解必为多目标决策的非劣解。

该定理可用K—T条件证明 。

该定理是将多目标规划转化为单目标规划后，用图象或单纯形方法求解，但也有一定的局限性，对于多维情况则很难求解。

3 小结

本文通过对了运筹学中一个经典的线性规划例子作为引例进行研究，从教学角度对线性规划（LP）、目标规划（LGP）及多目标规划（MLP）这三种常见的规划的概念、内在关系进行研究，发现在实际中线性规划和目标规划都可以转化为多目标规划来进行优化，不仅能将这三种规划融汇贯通理解本质和含义，也为其它规划问题的拓展研究提供理论和方法上教学借鉴。

从理论上看：线性规划（LP）、目标规划（LGP）以及多目标规划（MLP）三者有着联系，LGP是LP的推广，显然包括LP作为其特殊情况；在LGP中的优先级就相当于MLP中的权重，所以在某种意义上来说，MLP是LGP问题的推广；所以LP、LGP都可以转化为MLP来进行求解。

从实践上看：在日常生活中所遇到的实践问题中，大多数都涉及到多个目标和要求的，虽然有的可直接用LP和LGP去求解，但LP与LGP所解决的问题多限于一定变量个数，如遇大规模优化问题，LP与LGP解决起来不太灵活；而对于MLP问题求解，我们大多可用软件来实现，但对MLP求解中，由于权重取的不同，则结果也不尽相同，所以我们可以多取一些权重的形式多进行几次计算，找一个切合实际的满意解即可。（因为在解决实际问题中，满意解往往比最优解更具有现实意义）。

了解的这三种规划的概念、联系，也为以后进一步学习随机规划、模糊规划做了铺垫作用，这些规划在理论上、方法上都是同出一辙，只是用不同的研究工具对规划问题进行研究，是的对实际问题的优化问题的研究和讨论更加与实际问题跟贴切。

[1] 运筹学教材遍写组.运筹学（修改版）[M].北京：清华大学出版社，1990.

[2] 钱伟懿，杨菊，等.求解多目标规划问题的一种新的群体搜索算法[J].辽宁师范大学学报，2007，（2）：141-143.

[3] 刘旺梅，韩旭里.一种求解多目标规划的新方法[J].系统工程与电子技术，2001，（8）：15-17.

[4] 张建中，许绍吉.线性规划[M].北京：科学出版社，1999.

[5] 邱箢华.管理决策与应用熵学[M].机械工业出版社，2000.