氢负离子在变形球面附近的光剥离*

李绍晟 王德华

(鲁东大学物理与光电工程学院,烟台 264025)

(2012年7月10日收到;2012年9月28日收到修改稿)

1 引言

近几年来,随着强场和表面物理的发展,原子、分子、离子与外场和表面的相互作用引起了人们的广泛关注.由于剥离阈附近氢负离子的光剥离可以提供一个很好的自由电子的相干电源,外场或表面可以调控电子波的传播,所以负离子体系在外场和表面附近光剥离的研究引起了人们的极大兴趣.自从Bryant等[1]报道了氢负离子在静电场中的光剥离截面出现振荡结构以后,对于负离子在各种不同的外场中光剥离问题的理论和实验研究如雨后春笋般地涌现出来.主要的研究有：1989年,Du[2]用量子力学的方法研究了氢负离子在平行的电场和磁场中的光剥离.1993年,Peters和Delos[3,4]研究了在相互垂直的电场和磁场中氢负离子的光剥离问题.1996—1997年,Liu和Wang等将文献[2—4]的研究进行了推广,探讨了当电场和磁场成任意夹角时氢负离子的光剥离截面的振荡问题[5,6].最近几年,由于氢负离子被用来探测吸附物的态寿命和反向散射中的电荷转移,表面附近氢负离子的光剥离问题也引起了人们极大的兴趣.首先,Yang等[7,8]利用闭合轨道理论研究了氢负离子在弹性界面附近的光剥离;其次,文献[9]发展了理论模型成像方法,并且对同一体系进行了研究,得到的结果和闭合轨道理论结果符合得比较好.文献[10—21]将弹性表面推广到金属面,研究了氢负离子在金属面附近的光剥离问题.在前人的研究中,主要针对氢负离子在平面附近的光剥离问题进行研究,对于在曲面附近,氢负离子光剥离问题的研究,研究报道相对较少.最近,Haneef等[22]对氢负离子在球面附近光剥离的电子能谱进行了研究.我们研究小组对氢负离子在金属球面附近光剥离电子的运动和体系的光剥离截面进行了计算和分析[23].但是,当平面和球面相结合时,氢负离子光剥离问题的研究,迄今还未见报道.本文在文献[22]工作的基础上,采用理论模型成像方法,对氢负离子在变形球面附近的光剥离问题进行了研究.研究结果表明：入射光子的能量和H-到球面的距离以及球面半径对光剥离电子通量分布和光剥离截面的振荡结构都会产生很大的影响.在距离z轴比较近的区域,球面效应起主要作用,平面效应可以忽略;距离z轴较远的区域,平面效应和球面效应共同起作用,此时电子通量分布和光剥离截面变得更加复杂.因此,我们可以通过改变负离子到球面的距离以及球面的半径对氢负离子的光剥离进行调控.我们的结果对于研究负离子体系在曲面附近的光剥离及光剥离显微问题的实验研究具有一定的参考价值.

2 理论模型和公式推导

2.1 物理图像描述

该体系的物理模型如图1所示.变形球面可以看作是由一个平面将中间部分弯曲成一个半径为rc的半球面以后形成的.假定氢负离子到球面顶点距离为d,球面半径为rc,观测平面到球面顶点的距离为L,L通常为几千原子单位.激光的极化方向沿z轴的正方向.氢负离子可以看作是单电子体系,即电子被一个短程势松散地束缚在氢原子附近.氢负离子在变形球面附近光剥离的物理图像可以这样来描述：当一束激光照射到氢负离子,氢负离子吸收了光子能量以后,电子便会挣脱氢原子的束缚,从而剥离出去.假定剥离电子位于图1中的点1处,电子以电子波的形式沿着各个方向向外传播,当电子波传播到平面和球面附近时,会发生反射.反射波继续向外传播.可以将反射波看作是由像电荷2和3发出的.因此,氢负离子在变形球面附近的光剥离过程,要比单纯存在球面时复杂.但是进一步的分析发现,在观测平面上的每一点处,并不总是由三列电子波同时到达.在距离z轴较近的区域,只有直接从剥离电子出射的电子波和从球面反射后的电子波到达观测屏幕.此时,氢负离子的光剥离过程与在单一球面附近的光剥离是一致的[22].而距离z轴较远的区域,从剥离电子出射的电子波和从球面和平面反射后的电子波同时到达观测屏幕,此时观测平面上的波函数可以看作是由三列电子波的线性组合.假定观测点到z轴的距离为r′,经平面反射后出射的电子波能够到达观测屏的位置距离z轴最短距离为r0,由几何关系证明得到

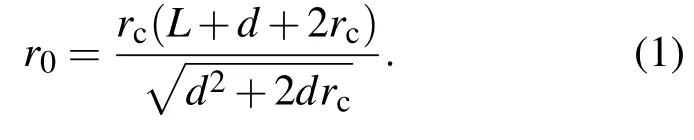
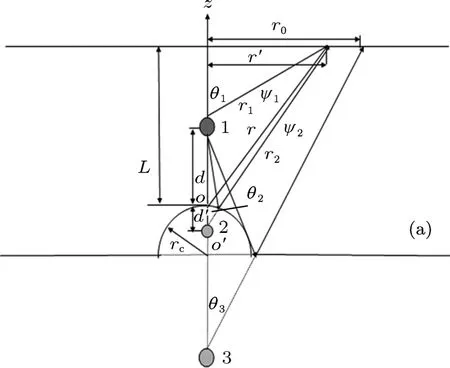
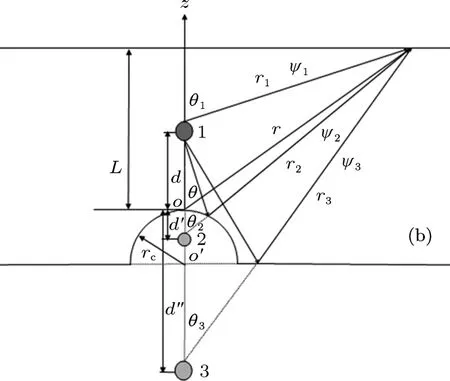
图1 氢负离子在变形球面附近光剥离的物理图像 位于1,2,3处的电荷代表剥离电子和剥离电子分别由于球面效应和平面效应而形成的像;三列出射波分别为ψ1,ψ2,ψ3;观测屏到球面顶点的距离为L,r0为平面效应作用的最小半径;(a)r′≤r0时,只有两列出射波到达观测屏上一点;(b)当r′＞r0时,三列出射波同时到达观测屏上一点

2.2 剥离电子波函数

从图1(a)可以清楚地看到,当观测屏上一点距z轴距离r′小于r0(即r′≤r0)时,只有直接出射的电子波和从球面反射后的电子波到达观测屏幕.此时剥离电子的波函数与只存在球面时的情况完全相同[22]：

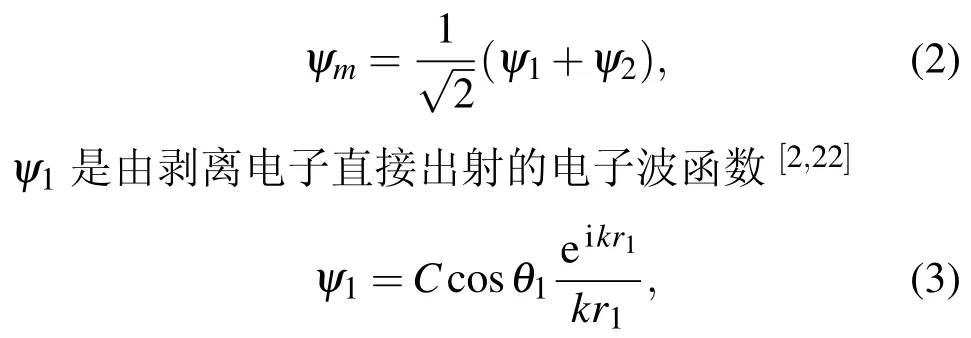
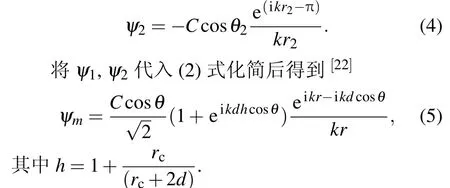
当观测屏上一点距z轴距离r′大于r0(即r′＞r0)时,从图1(b)可以看出,在观测平面上一点会有三列电子波同时到达.其中ψ1是电子被剥离以后传播了r1距离后直接传播到观测屏的;ψ2可以看作是电子以π-θ2的角度入射到球面后,经过球面反射后到达观测屏的;ψ3是电子沿着以π-θ3方向入射到平面之后,经过平面反射后到达观测屏的.根据理论模型成像方法,ψ2,ψ3可以分别被看作是从像电荷2,3发出的电子波传播了距离r2,r3后到观测屏的.因此,到达观测屏的总的电子的波函数可以看作是由ψ1,ψ2,ψ3三个波函数的线性叠加：

其中ψ1是由剥离电子直接出射的电子波函数[2,22],ψ2可以看作是剥离电子波函数经过球面发生一次反射以后形成的,ψ1,ψ2的表达式由(3),(4)式给出;ψ3是剥离电子波函数经过平面反射以后形成的,当电子波被平面反射后,也会产生π的相移并且波函数的系数中会出现一个“-”号,ψ3可以表示为

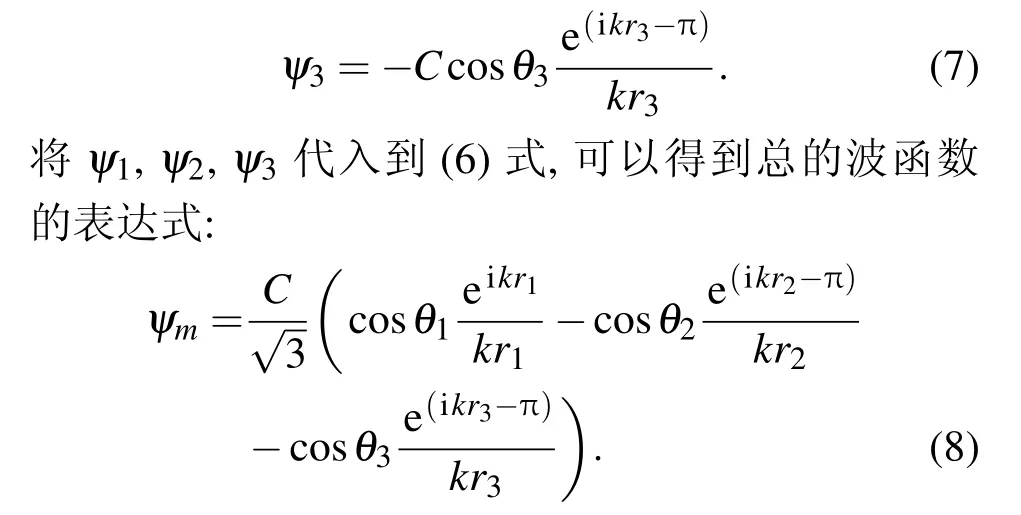
在氢负离子的光剥离显微实验中,氢负离子到观测屏的距离L≫d,因此,可以采用大距离近似法.其中θ1≈θ2≈θ3≈θ,θ为r与z轴的夹角.在(8)式中,波函数中的振荡项主要来源于指数函数,因此指数函数中的r1,r2,r3可以近似化简为：r1≈r-dcosθ,r2≈r+d′cosθ,r3≈r+(d+2rc)cosθ.在分母中,r1≈r2≈r3≈r.其中r是球面顶点与观测点之间的距离.于是到达观测屏的总的剥离电子的波函数可以化简为

2.3 光剥离电子通量分布

由量子力学知识可知,电子通量的计算公式为[22]

将剥离电子波函数(10)式代入后,可以得到各个区间光剥离电子通量沿径向方向的分布为

由于观测屏是在与z轴垂直的平面上,因此光剥离电子通量在观测屏上的分布为

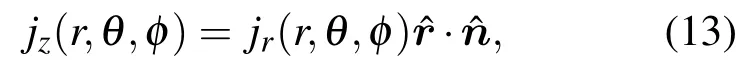
其中是沿径向方向的单位矢量,是与观测屏垂直方向的单位矢量.因为观测屏沿与z轴垂直的方向,因此

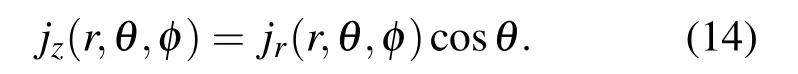
将上式中的球坐标用空间直角坐标表示,可以得到观测屏上任一点(x,y)处,光剥离电子通量分布的表达式：

2.4 光剥离截面

微分散射截面与光剥离电子通量之间的关系为[22]

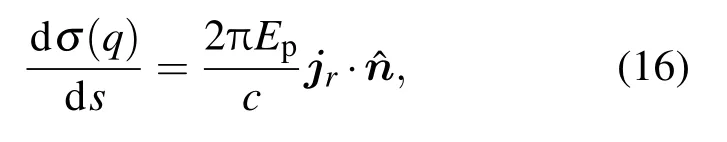
3 计算结果和分析

利用(15)式,我们给出了光剥离电子通量在观测屏上的分布图像.图2给出了光剥离电子通量jz随入射光子能量变化的三维图像.入射光子的能量Ep=E+Eb,E为剥离电子的能量.在计算中,我们假定氢负离子到球面的距离d=50 a.u.,球面半径rc=50 a.u.,观测屏到球面的距离L=1000 a.u.保持不变.在此种情况下,r0=663.95 a.u.当观测屏上一点到达z轴的距离r′≤r0时,电子通量分布与只有球面的情况一致[22];当r′＞r0,电子通量分布是由直接到达观测屏的电子波和被球面和平面反射后到达观测屏的三列电子波发生干涉引起的.从图2可以看出,随着入射光子能量的增加,光剥离电子的通量分布变得越来越复杂.当入射光子能量较小的时候,中心位置是个波谷,光剥离电子的通量分布比较简单,如图2(a)所示.随着入射光子能量的增大,波谷的位置略有升高;当入射光子能量再增大的时候,波谷的位置慢慢降低;当入射光子能量进一步增大,波谷的位置又慢慢升高,光剥离电子的通量分布中出现了一系列的振荡结构,如图2(d)所示.

图2 氢负离子在变形球面附近光剥离电子的通量分布 jz随入射光子能量变化的三维图像,其中d=50 a.u.,rc=50 a.u.,L=1000 a.u.(a)Ep=1.0 eV;(b)Ep=2 eV;(c)Ep=3 eV;(d)Ep=4 eV

为了更清晰地看出光剥离电子通量在观测屏上的分布情况,我们给出了对应图2的三维等高线轮廓图,如图3所示.从图3可以看出,等高线轮廓图中出现了一系列明暗相间的同心的干涉条纹.靠近中心干涉条纹(r′≤r0)是由直接到达观测屏的电子波和被球面反射后到达观测屏的两列电子波发生干涉引起的.靠近外侧的(r′＞r0)干涉条纹则是由直接到达观测屏的电子波和被球面和平面反射后到达观测屏的电子波发生干涉引起的.图中的亮条纹是电子波发生干涉加强以后形成的,对应图2三维图中的波峰;暗条纹是电子波发生干涉减弱以后形成的,与图2三维图中的波谷相对应.随着入射光子能量的增加,等高线轮廓图中干涉条纹的条数增加,表面观测屏上剥离电子的通量分布变得越来越复杂.

图3 氢负离子在变形球面附近光剥离电子的通量分布随入射光子能量变化的等高线轮廓图,其中d=50 a.u.,rc=50 a.u.,L=1000 a.u.(a)Ep=1 eV;(b)Ep=2 eV;(c)Ep=3 eV;(d)Ep=4 eV

图4给出了电子通量沿y轴方向的二维分布.在计算中,令(15)式中的x=0,从而给出了jz随y的变化的二维图像.其中入射光子的能量及其他的一些几何参数与图2和图3中的相同.从图4中可以看出,距离z轴较近的区域,即y≤y0=663.95 a.u.时,电子通量的分布与只有球面的情况一致[22],平面效应可以忽略;当y＞y0,球面效应和平面效应共同起作用,电子通量分布变得非常复杂,振荡峰的数目增加.从图中还可以进一步看出：随着光子能量的增加,通量分布中振荡峰的数目增加,振荡结构变得越来越复杂,并且振荡的振幅先增加,然后减小;最后慢慢升高.在y＞y0区域,电子通量分布中振荡结构的频率随光子能量的增加而增大.

图4 氢负离子在变形球面附近 jz随入射光子能量变化的二维图像,其中d=50 a.u.,rc=50 a.u.和L=1000 a.u.保持不变(a)Ep=1 eV;(b)Ep=2 eV;(c)Ep=3 eV;(d)Ep=4 eV

图5 实线表示氢负离子在变形球面附近光剥离电子通量 jz随球面半径变化的图像,虚线表示氢负离子在球面附近光剥离电子通量 jz随球面半径变化的分布曲线,其中d=100 a.u.,L=1000 a.u.,Ep=1 eV (a)rc=50 a.u.;(b)rc=100 a.u.;(c)rc=200 a.u.;(d)rc=1000 a.u.

为了进一步分析球面半径及平面反射对光剥离截面的影响,我们给出了氢负离子在变形球面附近的光剥离电子通量jz随球面半径的变化曲线,并且和氢负离子在球面附近光剥离电子通量的分布曲线进行了比较,如图5所示.其中入射光子的能量Ep=1 eV,氢负离子到球面的距离和到平面的距离相等,都取d=100 a.u.从图中可以看到,当球面半径rc很小的时候,氢负离子在变形球面附近的光剥离电子通量与氢负离子在球面附近光剥离电子通量曲线重合部分比较小,如图5(a)所示.但是随着球面半径rc的渐渐增大,氢负离子在平面附近和在变形球面附近的通量重合部分越来越大.当rc很大的时候,氢负离子在变形球面附近的光剥离电子通量和在球面附近光剥离电子通量曲线完全重合,如图5(d)所示.原因如下：当球面半径rc很小的时候,平面效应的截止半径r0比较小,平面效应对jz的贡献比较大;当rc增大的时候,平面效应的截止半径r0增大,平面效应的影响逐渐减小.例如：在图5(a)中,rc=50 a.u.时,r0=424.26 a.u.;当y≤y0=424.26 a.u.时,电子通量的分布与只有球面的情况一致[22];当y＞y0,球面效应和平面效应共同起作用,电子通量分布与只有球面的情况相差很大.在图5(b)中,rc=100 a.u.,此时r0=750.55 a.u.;只有当y＞750.55 a.u.时,电子通量分布与只有球面存在时的通量分布有一定的差别;随着rc的渐渐增大,r0逐渐增大,电子通量分布与只有球面存在时的通量分布的差别越来越小.当rc=1000 a.u.时,r0=6764.75 a.u.,此时的电子通量分布与只有球面存在时的完全相同,平面效应可以完全忽略.

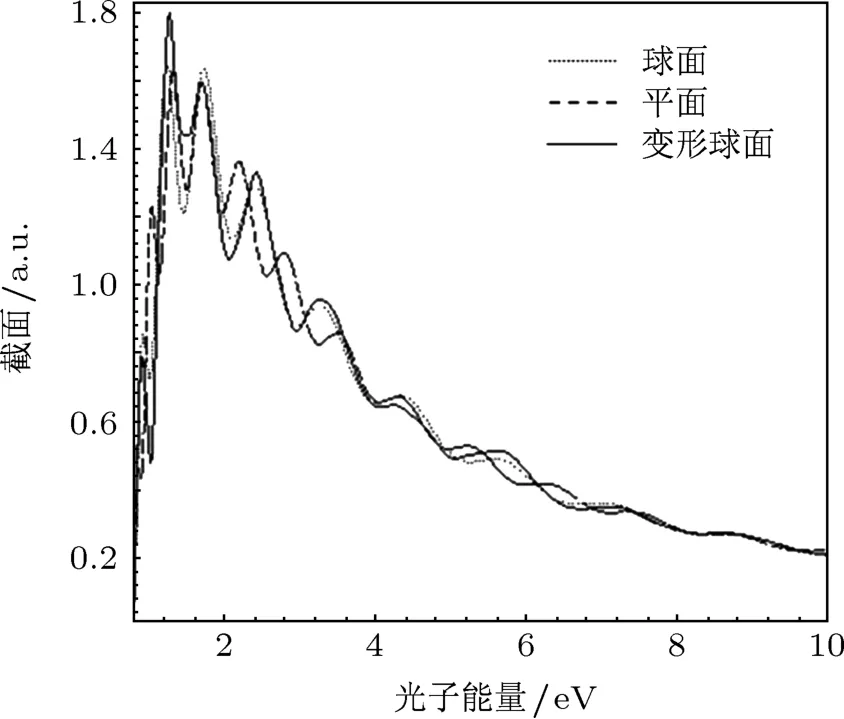
图6 氢负离子在变形球面附近光剥离截面、球面附近的光剥离截面和在平面附近的光剥离截面,其中离子到表面的距离d=50 a.u.,球面半径rc=100 a.u.

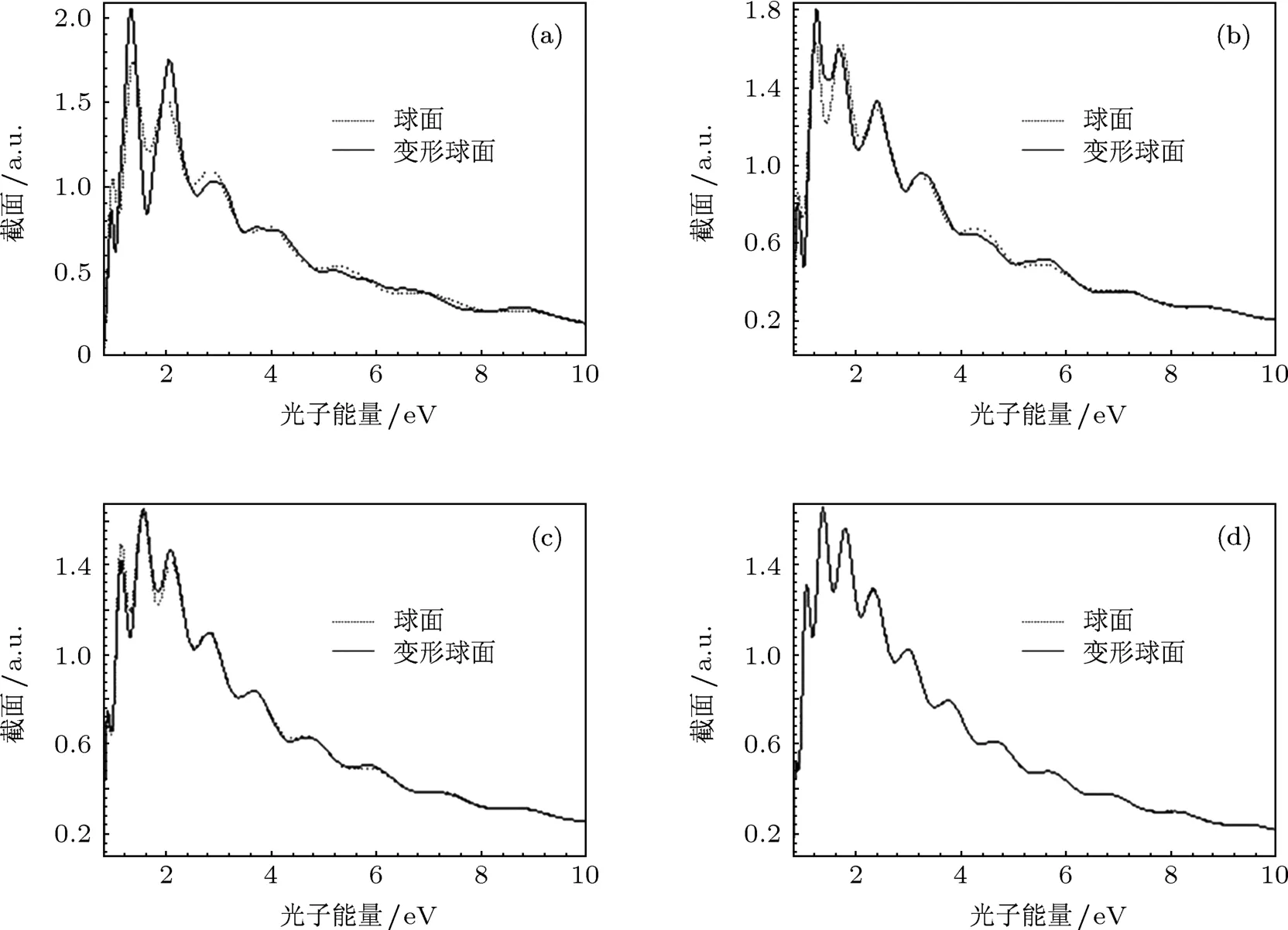
图7 d=100 a.u.,L=1000 a.u.时的光剥离截面 (a)rc=50 a.u.;(b)rc=100 a.u.;(c)rc=200 a.u.;(d)rc=1000 a.u.

借助于数值积分,我们给出了氢负离子在变形球面附近的光剥离截面,如图6中的黑色实线所示.图6中的点线和虚线分别表示氢负离子在球面附近的光剥离截面和在平面附近的光剥离截面[6].在计算中,选取离子到表面的距离d=50 a.u.,球面半径rc=1000 a.u..结果表明：氢负离子在变形球面附近的光剥离截面的振荡振幅比在单一的球面附近或平面附近的振荡振幅增加.当入射光子能量比较小的时候,氢负离子在变形球面附近的光剥离截面和在球面附近或平面附近的光剥离截面相差较大,但是当入射光子能量比较大的时候,氢负离子在变形球面附近的光剥离截面与在球面附近或平面附近的光剥离截面比较接近.

图7给出了氢负离子在变形球面附近的光剥离截面随球面半径的变化图像.其中实线代表在变形球面附近的光剥离截面,点线表示在球面附近的光剥离截面[22].通过比较可以看出：当球面半径rc比较小的时候,氢负离子在变形球面附近的光剥离截面比在单一球面附近的光剥离截面的振荡要复杂,而且振幅要比在球面附近情况要大;随着rc的逐渐增大,氢负离子在变形球面附近的光剥离截面和在球面附近的光剥离截面的差别越来越小;当rc=1000 a.u.的时候,氢负离子在变形球面附近的光剥离截面和在球面附近的光剥离截面完全符合.

4 结论

借助于理论模型成像方法,本文对氢负离子在变形球面附近的光剥离进行了研究,推导出了光剥离电子通量的计算公式,重点探讨了球面效应和平面效应对氢负离子在变形球面附近光剥离电子通量分布和光剥离截面的影响.结果表明,变形球面中的平面部分只在一定范围内对氢负离子的光剥离过程产生影响.距离z轴比较近的区域,平面效应可以忽略;距离z轴较远的区域,平面效应和球面效应共同起作用,此时变形球面对负离子体系的光剥离会产生比较大的影响.当氢负离子到球面之间的距离一定,随着球面半径的增大,光剥离电子通量和光剥离截面的振荡结构变得更加复杂,振荡结构中的峰值增加,振荡频率加强.因此,我们可以通过改变球面的半径对氢负离子的光剥离进行调控.我们所选取的变形球面是由一个平面将中间部分弯曲成一个半球面以后形成的,因此在球面和平面的连接部分不存在衍射效应.迄今为止,氢负离子在曲面附近光剥离的实验研究还未见报道,希望我们的结果对于研究负离子体系在曲面附近光剥离的实验研究提供一定的参考价值.

[1]Bryant H C 1987Phys.Rev.Lett.58 2412

[2]Du M L 1989Phys.Rev.A 40 4983

[3]Peters A D,Delos J B 1993Phys.Rev.A 47 3020

[4]Peters A D,Delos J B 1993Phys.Rev.A 47 3036

[5]Liu Z Y,Wang D H,Lin S L,Shi W Z 1996Phys.Rev.A 54 4078

[6]Liu Z Y,Wang D H 1997Phys.Rev.A 55 4605

[7]Yang G C,Zheng Y Z,Chi X X 2006J.Phys.B 39 1855

[8]Yang G C,Zheng Y Z,Chi X X 2006Phys.Rev.A 73 043413

[9]Afaq A,Du M L 2007J.Phys.B：At.Mol.Opt.Phys.40 1309

[10]Zhao H J,Du M L 2009Phys.Rev.A 79 023408

[11]Rui K K,Yang G C 2009Surf.Sci.603 632

[12]Yang B C,Du M L 2010J.Phys.B 43 035002

[13]Tang T T,Wang D H 2011J.Phys.Chem.C 115 20529

[14]Han Y,Wang L F,Ran S Y,Yang G C 2010PhysicaB 405 3082

[15]Huang K Y,Wang D H 2010J.Phys.Chem.C 114 8958

[16]Wang D H 2011J.Appl.Phys.109 014113

[17]Wang D H,Wang S S,Tang T T 2011J.Phys.Soc.Jpn.80 094301

[18]Wang D H 2011Curr.Appl.Phys.11 1228

[19]Wang S S,Wang D H,Tang T T,Huang K Y 2011Acta Phys.Sin.60 053402(in Chinese)[王姗姗,王德华,唐田田,黄凯云2011物理学报60 053402]

[20]Wang D H,Tang T T,Huang K Y 2011Acta Phys.Sin.60 053203(in Chinese)[王德华,唐田田,黄凯云2011物理学报60 053402]

[21]Huang K Y,Wang D H 2010Acta Phys.Sin.59 932(in Chinese)[黄凯云,王德华2010物理学报59 932]

[22]Haneef M,Ahmad I,Rahman A 2011J.Phys.B 44 195004

[23]Wang D H,Li S S 2012J.Phys.Soc.Jpn.81 074301