非Lipschitz条件下由一般鞅驱动的倒向随机微分方程解的存在性
2013-02-24李师煜高武军刘且根
李师煜,高武军,刘且根
(1.江西理工大学理学院,江西赣州341000;2.南昌大学电子信息工程系,南昌330031)
非Lipschitz条件下由一般鞅驱动的倒向随机微分方程解的存在性
李师煜1,高武军1,刘且根2
(1.江西理工大学理学院,江西赣州341000;2.南昌大学电子信息工程系,南昌330031)
经典的倒向随机微分方程以布朗运动做为干扰源,布朗运动是一种理想化的随机模型,从而使倒向随机微分方程的应用受到了限制.文中研究了以连续局部鞅为干扰源的倒向随机微分方程,在生成元满足一种非Lipschitz条件下,通过构造一个函数列的方法,利用Lebesgue's控制收敛定理和常微分方程的比较定理,证明了其解是存在的并且是唯一的,对经典的倒向随机微分方程进行了推广.
连续局部鞅;倒向随机微分方程;解的存在性和唯一性
0 引言
Pardoux和Peng[1]在1990年给出了非线性形式的倒向随机微分方程并且在Lipschitz条件下证明了解的存在性和唯一性,从此之后,倒向随机微分方程(BSDE)理论和应用得到了飞快发展,倒向随机微分方程现在已经成为研究随机最优控制、数理金融、偏微分方程、随机微分效用等的强大工具.
经典的倒向随机微分方程理论以布朗运动为干扰源,而布朗运动是一种理想化的随机模型,致使经典的倒向随机微分方程的应用受到了限制.一方面,许多学者研究了以其他随机过程为干扰源的倒向随机微分方程,其中李娟[2]和王湘君[3]分别研究了以连续半鞅和连续局部鞅为干扰源的倒向随机微分方程,在系数满足Lipschitz条件下证明了解的存在性和唯一性,其它研究工作可参见文献[4-6].另一方面,很多学者试图弱化生成元的Lipschitz条件和终端条件的可积性来改进Pardoux和Peng的关于解的存在唯一性,做过这方面研究的有:Fan[7-8],Lepeltier[9],Man[10],Wang[11-12],Chen[13],特别地,Fan[8]给出了一种非Lipschitz条件下解的存在唯一性结果.文中首先研究由连续局部鞅驱动的倒向随机微分方程在Fan[8]非Lipschitz条件下解的存在唯一性,通过构造一个函数列的方法,利用Lebesgue's控制收敛定理和常微分方程的比较定理,证明了其解是存在的并且是唯一的,对经典倒向随机微分方程进行了推广.
1 主要结果
令(Ω,F,{Ft}t≥0,P)为一个带信息流的完备的概率空间,且流{Ft}t≥0满足通常条件,记P为可料σ域.M={Mt,Ft∶0≤t<∞}为一个连续局部鞅,并且M0=0,
首先给出几个相关记号:
(1)用LM(0,T;Rn)表示所有使得的Ft-适应的Rn值的过程x=x(s)的集合.当n=1时简记为LM.
(2)用L′M(0,T;Rn×d)表示所有使得的Ft可料的Rn×d值的过程y=y(s)的集合.当n=d=1时简记为
(3)用L2(Ω,FT,P;Rn)表示所有满足+∞的FT-可测的Rn值的随机变量ξ的集合.当n= 1时简记为L2(Ω,FT,P).
现在给出以下的主要假设:
(H1)ξ∈L2(Ω,FT,P);
(H2)M={Mt,Ft∶0≤t<∞}为具有零初值的连续局部鞅,具有可料表示性,且

其中,u(·),v(·)∶[0,T]→R+,且满足

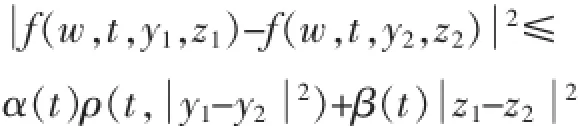
其中,α(·),β(·)∶[0,T]→R+且ρ(·,·)∈S[T,a(·),b(·)],S[T,a(·),b(·)]={k(·,·)∶[0,T]×R+→R+},且满足下面的两个条件:
(1)对固定的t,k(t,·)是连续的,单调不减的凹函数,k(t,0)=0,k(t,u)≤α(t)+β(t)u.
(2)微分方程u′(t)=-k(t,u),t∈[0,T],u(T)=0有唯一的解u(t)=0,t∈[0,T].

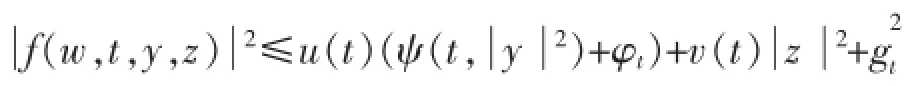
其中,ψ(·,·)∈S[T,a(·),b(·)],u(·),v(·)∶[0,T]→ R+,且是非负的Ft可测的过程,且满足E[M>t)2]<+∞.
以下,我们将讨论如下形式的一维倒向随机微分方程:
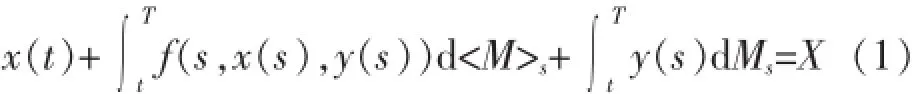
其中,x(s)为Ft适应的过程,y(s)为Ft可料的过程,X∈L2(Ω,FT,P),{Mt,Ft;0≤t<+∞}满足(H2),函数f∶Ω×[0,T]×R×R→R满足(H3).
定理1假设0<T<+∞,函数f∶Ω×[0,T]×R×R→R满足(H5)和(H6),则倒向随机微分方程(1)存在唯一一组适应解(x(s),y(s))0≤t≤T∈LM×L′M.
2 引理
为了证明定理1,我们还需要用到下面的引理.
引理1假设0<T<+∞,f满足(H7),(yt,zt)t∈[0,T]是倒向随机微分方程(1)的解,那么存在两个正数C1和C2,使得对t∈[0,T]
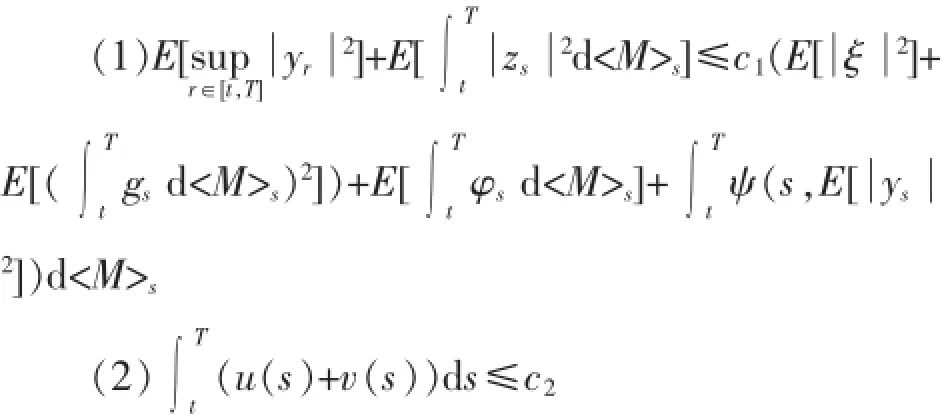
引理2假设0<T<+∞,ξ∈L2(Ω,FT,P),f满足(H4)和(H6)成立,那么倒向随机微分方程(1)存在唯一的解.
现在我们假设0<T<+∞,ξ∈L2(Ω,FT,P),f满足(H5)和(H6),构造Picard序列如下:设x0(t)=0,{xn(t),yn(t)∶0≤t≤T}∈LM×LM′,由如下的倒向随机微分方程所定义:

引理3假设0=T0<T1<T2<…<TN-1<TN,在定理1的假设下,对t∈[TN-1,TN],n,m≥1则

引理4在定理1的假设下,则存在常数K≥ 0,使得对n≥1,t∈[TN-1,TN],有成立.
注:以上4个引理的证明参见文献[7].
3 定理1的证明
存在性:定义一个函数列{φn(t)}n≥1如下:
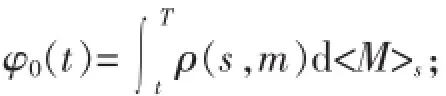

由引理4,对t∈[TN-1,TN],可得:
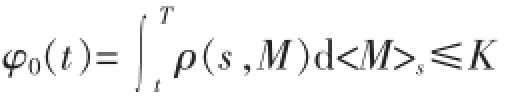
进一步可得,
0≤φn+1(t)≤φn(t)≤…≤φ1(t)≤φ0(t)≤K
因此,函数列{φn(t)}n≥1的极限存在,设其为φ(t).
对式(4)取极限,由Lebesgue's控制收敛定理可得,

由假设(H5)可得,φ(t)=0,t∈[TN-1,T].

因此,
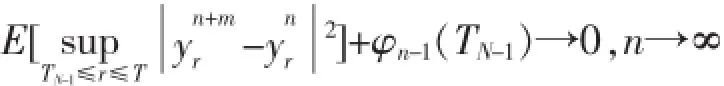
用TN-2,TN-1和yTN-1替换引理1-4中的TN-1,T和ξ,重复以上证明过程,即知At∈[0,T],(yt,zt)是倒向随机微分方程(1)的解.
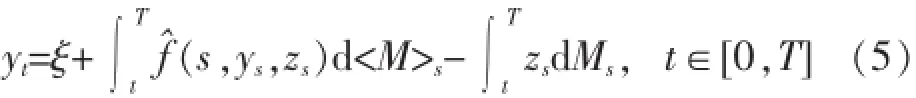
由引理1,可得

用TN-2和TN-1分别替换TN-1和T,重复以上证明过程,即知在整个区间[0,T],解是唯一的.
4 结语
文中研究了以连续局部鞅为干扰源的倒向随机微分方程,在生成元满足一种比Lipschitz条件更弱的条件下,证明了解的存在性和唯一性,对经典的倒向随机微分方程进行了推广,从而拓广了其在其它领域中的应用.此类倒向随机微分方程还有很多值得研究的地方,后续的研究可以从以下两方面进行:
(1)可以开展对此类倒向随机微分方程性质的研究,比如比较定理.
(2)可以讨论此类倒向随机微分方程在金融衍生产品期权定价的应用.
[1]Pardoux E,Peng S.Adapted solution of a backward stochastic differential equation[J].Systems&Control Letters,1990,14(1): 55-61.
[2]李娟.由一般鞅驱动的倒向随机微分方程[J].山东大学学报:理学版,2005,40(4):70-76.
[3]王湘君.由连续半鞅驱动的倒向随机微分方程[J].数学杂志,1999,19 (1):45-50.
[4]李师煜,高武军.由连续局部鞅驱动的倒向随机微分方程的解[J].江西理工大学学报,2009,30(5):71-73.
[5]Chen S.Lp solutions of one-dimensional backward stochastic differential equations with continuous coefficients[J].Stochastic Analysis and Applications,2010(28):820-841.
[6]Kobylanski M.Backward stochastic differential equations and partial differential equations with quadratic growth[J].Annals of Probability,2000(28):558-602.
[7]Fan S J,Jiang L.Finite and infinite time interval BSDEs with non-Lipschitz coefficients[J].Statistics&probability letters,2010, 80(11):962-968.
[8]Fan S J,Jiang L,Tian D J.One-dimensional BSDEs with finite and infinite time horizons[J].Stochastic Processes and their Applications, 2011,121(3):427-440.
[9]Lepeltier J P,San Martin J.Backward stochastic differential equations with continuous coefficient[J].Statistics&Probability Letters,1997,32(4):425-430.
[10]Mao X.Adapted solutions of backward stochastic differential equations with non-Lipschitz coefficients[J].Stochastic Processes and Their Applications,1995,58(2):281-292.
[11]Wang Y,Huang Z.Backward stochastic differential equations with non-Lipschitz coefficients[J].Statistics&Probability Letters,2009,79(12):1438-1443..
[12]Wang Y,Wang X.Adapted solutions of backward SDE with non-Lipschitz coefficients[J].Chinese Journal of Applied Probability and Stastistics,2003,19(3):245-251.
[13]Chen Z,Wang B.Infinite time interval BSDEs and the convergenceofg-martingales[J].Journal-Australian Mathematical Society Series A,2000,69(2):187-211.
Adapted solutions of backward stochastic differential equations driven by general martingale under non-Lipschitz condition
LI Shi-yu1,GAO Wu-jun1,LIU Qie-gen2
(1.Faculty of Science,Jiangxi University of Sciences and Technology,Ganzhou 341000,China;2.Department of Electronic and Information Engineering,Nanchang University,Nanchang 330031,China)
The classical backward stochastic differential equations(BSDE)theory is taken the Brownian motion as the noise source,but the Brown motion is one kind of extreme idealized model,which causes limitations of the BSDE theory in application.This paper studies the backward stochastic differential equation which is taken continuous local martingale as the noise source.The authors of the paper conclude a general existence and uniqueness of the solutions under non-Lipschitz condition on the generator by adopting the construction of function sequence,Lebesgue's dominated convergence theorem and the comparison of ordinary differential equation.The authors have also conducted a substantial extension of the classical backward stochastic differential equations.
continuous local martingale;backward stochastic differential equation;existence and uniqueness of the solution
O211.6
A
2095-3046(2013)03-0093-04
2013-01-28
国家自然科学基金资助项目(61262084)
李师煜(1983-),男,讲师,主要从事随机分析等方面的研究,E-mail:lishiyu83@163.com.
