对毫米波末制导雷达两点源干扰效能分析研究
2014-07-11贾仁耀韩书键孟令杰
贾仁耀,韩书键,孟令杰
(电子工程学院,安徽 合肥 230037)
0 引言
毫米波末制导导弹因其制导精度和抗干扰能力方面的优势,愈来愈多地应用于现代战争。两点源干扰是诱偏毫米波末制导导弹、降低其命中率的重要手段之一,而两点源干扰的效能分析是衡量干扰效果的一种重要方法。本文在分析两点源干扰原理的基础上,提出了两点源干扰效能指标,建立了相关指标的效能分析模型,可为两点源干扰效能评估提供科学的依据,并对改善两点源干扰效果有现实意义。
1 对毫米波末制导雷达对抗技术
毫米波电子对抗技术主要分为有源干扰和无源干扰,本文着重对有源干扰中的两点源干扰进行分析。两点源干扰是指利用两个干扰设备的配合完成对毫米波末制导雷达的干扰。毫米波末制导雷达普遍采用单脉冲角跟踪技术,具有很强的抗单点源角度欺骗干扰的能力,如果仅使用单点源干扰,干扰效果并不是很理想,且干扰源自身容易受到导弹的攻击。因此,常用两点源(或多点源)干扰方式来对抗单脉冲雷达角跟踪系统。这种干扰方式可以避免导弹对干扰装备的跟踪,在保护目标的同时,亦可以起到保护装备的作用。
2 两点源相干干扰效能分析模型
两点源相干干扰,是指在被保护目标附近设置两个干扰辐射源,干扰信号频率相同而且相位相关,造成导弹导引头跟踪目标的不确定而误判目标为两点源之外的某一点,致使导弹偏离跟踪目标而攻击失败。
由于干扰信号在功率和距离上的优势,可以忽略被保护目标反射的雷达信号。假设干扰源1配置在目标附近,并以干扰源1为坐标原点建立坐标系,如图1所示。某时刻t,导弹位于A(x,y)点,两点源对导引头的张角为θsj,干扰源1、2的距离为d,导弹跟踪方向与干扰源1方向的偏角为Δθj,O1为导弹最后落点。
干扰目的是使导弹落点偏离干扰源1,因此选取Δθj/θsj评估两点源干扰的效果。不考虑信号衰减,两干扰源辐射电场到达导弹导引头处的场强分别为[1]:
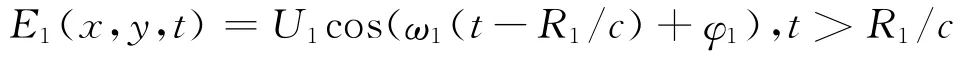

两点源干扰时导弹与干扰源的位置关系
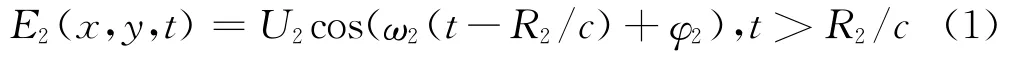
式中,ω1、ω2为两干扰源的角频率,φ1、φ2为两干扰源初始相位,U1、U2为两干扰源信号的振幅,c为光速。
相干干扰时,导弹跟踪方向与干扰源1方向的偏角Δθj为:
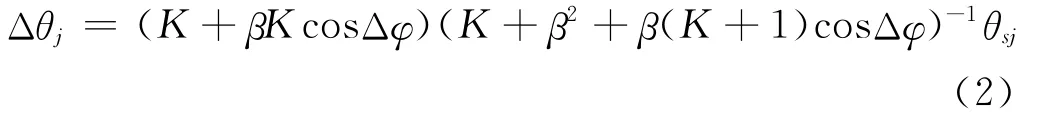
式中,K=ω1R2(ω2R1)-1,Δφ=φ1-φ2,β=U2/U1。
设两干扰源频率上保持一致,离导弹的距离差产生的相位差保持恒定,则Δθj为:
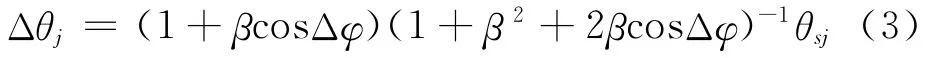
上述公式的适用范围一般为θsj/θ0.5≤0.8~0.9,β≤0.9或β≥1.1。由式(3)可得干扰效果 Δθj/θsj与Δφ、β的关系如图2所示。

图2 干扰效果与Δφ、β的关系示意图
可见,导弹偏离干扰源1的程度随Δφ先增大后减小,在Δφ=180°左右,Δθj/θsj最大;而β越大,导弹偏离干扰源1越远。考虑到β≤0.9或β≥1.1,当β≥1.1时,导弹偏离干扰源1最远,但这样有可能距离干扰源2较近;β≤0.9时,距离干扰源1和2都较远。因此,在实际使用两点源相干干扰时,相位差Δφ和振幅比β的选取尤为重要:1)为使导弹最大限度偏离干扰源1,应取Δφ=180°;2)若被保护目标价值巨大,则可取β≥1.1,导弹落在干扰源2的右侧,但有可能对干扰源2造成毁伤;若要保全干扰源2,则取β≤0.9,导弹落在两干扰源之间。
3 两点源非相干干扰效能分析模型
两点源非相干干扰,是指在末制导雷达的角度分辨范围之内,两点源同时施放干扰信号,但信号各自独立,彼此不相干。假设两点源位置关系仍如图1所示,则两点源非相干干扰时导弹跟踪方向与干扰源1的偏角为:
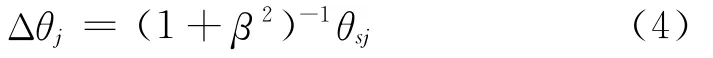
非相干干扰时,末制导雷达跟踪方向与两干扰源的信号强度有关。当信号强度相等,即β=1时,导弹跟踪两干扰源的中间;当只有一个干扰源开机时,即对应β=0或β=∞的情况,导弹跟踪开机的干扰源。
若己方被保护目标价值巨大,不惜以干扰源为代价保护目标,则应当使干扰源2开机,干扰源1关机,诱使末制导导弹飞向干扰源;若被保护目标价值相对较小,则β应取值在1附近,并适当增加两干扰源之间距离(即d/2大于导弹的杀伤半径),导弹将落在两干扰源之间。
4 闪烁干扰效能分析模型
当毫米波末制导雷达同一波束内有2个干扰源时,这两个干扰源周期交替发射干扰信号,就会使雷达波束中心交替指向两个干扰源,这就是双机闪烁干扰的原理。闪烁干扰将使导弹不停地摆动,破坏末制导雷达角跟踪系统的正常工作,导致其不能稳定地跟踪目标,或干扰关机后丢失目标,最终降低毫米波末制导武器系统的命中精度。
4.1 闪烁干扰成功的条件
闪烁干扰要成功需满足以下条件:1)有较大的干信比;2)末制导雷达无法从距离、速度和角度上分辨两目标。
当两干扰源与末制导雷达的距离大于雷达距离分辨率时,末制导雷达将从距离上分辨出两目标。当两目标之一脱离末制导雷达波束时,雷达将从角度上分辨目标,只跟踪其中一个目标。因此,要有效实施闪烁干扰,双机应始终处于毫米波末制导雷达的主波束内,与雷达的张角应不大于雷达的分辨角[2-3]。
4.2 闪烁干扰下导弹的命中概率
闪烁干扰时导弹与干扰源的位置关系如图3所示。
由导引头的动态跟踪特性可知,导弹运动轨迹与导弹雷达天线的分辨角θ密切相关:当θsj<θ时,雷达天线指向位于干扰源之间的能量重心方向;当θsj≥θ时,闪烁干扰失效,导引头重新搜索目标,分辨出两点源,并能稳定跟踪其一,这时导弹以最大过载aw向目标运动,取aw为过载平均值:
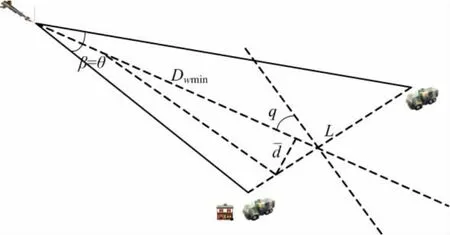
图3 闪烁干扰时导弹与干扰源的位置关系

式中,导弹惯性系数au=0.5~0.7;重力加速度g=9.8m/s2;nw为导弹所处高度允许的过载。
干扰装备运动速度相对导弹来说可以忽略不计。导弹能修正的距离误差为:
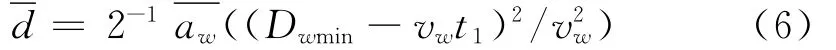
式中,Dwmin为时导弹与目标之间的距离;t1为重新搜索目标至分辨识别目标所用时间;vw为导弹速度。
两点源之间距离为L,有:


式中,αr是导弹自身的均方根误差。
因此,在受到闪烁干扰时,导弹一次射击对目标的杀伤概率为:
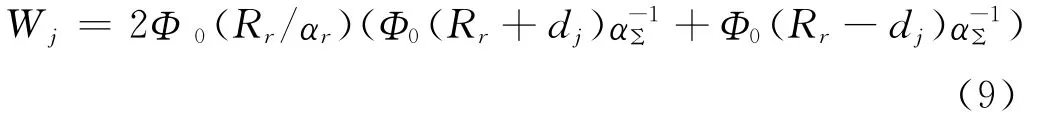
可知,导弹一次射击对目标的杀伤概率与两干扰源之间的距离有很大的关系。由于毫米波分辨单元很小,一般为2~5°,那么闪烁干扰两干扰源之间的间距L保持比较小,才能使闪烁干扰有效。
5 结束语
由于毫米波雷达导引头频带宽、自导波束角窄,实施有源干扰对侦察引导提出较高的要求。除有源干扰外,还可采用无源干扰的手段,将无源干扰物布放在较精确的空间位置,也可有效地干扰毫米波雷达末制导雷达。
[1]杨正,薛业飞,曹志耀.两点源诱骗反辐射导弹的效能评估模型研究[J].电光与火控,2007(3):19-21.
[2]侯民胜,樊晓明,洪善民.一种有效的角度欺骗干扰[J].信息化研究,2009(10):6-9.
[3]侯民胜,朱莹,樊晓明.单脉冲雷达干扰技术研究[J].现代电子技术,2009(15):1-3.
