两类矩阵多项式的逆矩阵的求法

赖新兴，肖清岚

（江西理工大学理学院，江西赣州341000）

两类矩阵多项式的逆矩阵的求法

赖新兴，肖清岚

（江西理工大学理学院，江西赣州341000）

矩阵的求逆是矩阵论中研究的重要问题，尤其是一些矩阵多项式的求逆问题．在求矩阵多项式的逆矩阵过程中，研究发现一些特殊矩阵多项式与其逆之间不仅有密切联系，而且有特殊的结构或形式．文中对两类矩阵多项式的逆矩阵求法进行了探讨，研究求逆的一些方法，得出两类矩阵多项式的求逆公式，并且对相关结论分别举例加以应用．使得这两类矩阵多项式求逆变得简单明了，相关问题也可以迎刃而解．对丰富矩阵多项式的求逆理论具有重要意义，对学习求逆知识也具有借鉴作用．

矩阵；矩阵多项式；逆矩阵

0 引言

矩阵是高等代数的主要研究对象之一，在自然科学、工程技术乃至社会科学中均广泛应用.而矩阵的求逆又是矩阵理论当中非常重要的问题，由于其解法灵活，综合性较强，能力要求较高，解决这类问题，要掌握各数学分支知识，并能综合运用各种数学技能，灵活选择合理的解题方法.在数学上，灵活运用从特殊到一般的思想，可以使很多难以解释的问题得到很好的解决.

关于矩阵的逆，在《高等代数》[1]或《线性代数》[2]的学习中就有了一定的认识，如何求逆矩阵一直是研究者探讨的问题.2002年黄光鑫[3]考虑伴随矩阵的情形得到一种求可逆矩阵新方法.2007年王丽霞[4]总结和归纳了求逆矩阵的几种求法.2008年邵逸民[5]对几类特殊矩阵的逆矩阵问题进行了研究，讨论了它们可逆的条件，分析了这些矩阵与其逆矩阵之间的关系，并给出了其逆矩阵的特征或求逆矩阵的公式.2010年王美莲和何翠竹[6]利用幂零矩阵和严格上三角形矩阵的性质得到了求其逆矩阵的一个简单公式，这为解决矩阵方幂的计算问题提供了方便.2011年蒋加清[7-8]利用多项式矩阵的初等行变换给出的r-循环矩阵和对称r-循环矩阵求逆的简便算法.同时很多文献对逆矩阵的其它特点和性质也进行了相关研究，已有诸多研究成果[9-15].但是对于一些矩阵多项式求逆的问题却一直没有很好的方法，文中讨论了两类矩阵多项式的求法，使得这两类矩阵多项式求逆的问题迎刃而解.

1 主要结果

定理1若n阶矩阵A满足A3-kE=0，矩阵B满足B=A2+mA+nE，m、n、k满足m3+k2+m3k-3mnk≠0，记d=n3+k2+m3k-3mnk，则B可逆，且有表达式：

证明由于A3＝kE，从而A4-kA=0，设B的逆矩阵为aA2+bA+cE，代入BB-1=E，则有（A2+mA+ nE）（aA2+bA+cE）=E.将A4-kA=0代入，化简得到（c+bm+an）A2+（ak+bn+mc）A+（amk+bk+cn）E=E.将系数进行对比得到：

与之对应有矩阵形式

当d=n3+k2+m3k-3mnk≠0，可以解出

得出B是可逆阵，且

得证.

定理2若n阶矩阵A满足A3-mA2-nE＝0，矩阵B满足B=A2+kE，其中m2k2+k3-2mnk+n2≠0，记Ω＝m2k2+k3-2mnk+n2，则B可逆，且

证明由于A3-mA2-nE＝0，从而A4-mA3-nA＝0，则有A3=mA2+nE，A4=mA3+nA＝m2A2+nA+ mnE，设B的逆矩阵为aA2+bA+cE，代入BB-1=E，则有（A2+kE）（aA2+bA+cE）=E.将A3=mA2+nE，A4= mA3+nA=m2A2+nA+mnE代入，化简得到

（m2a+ka+mb+c）A2+（na+kb）A+（mna+nb+kc）E=E.

将系数进行对比

与之对应有矩阵形式

当Ω＝m2k2+k3-2mnk+n2≠0，可以解出：

则可以得出B是可逆阵，且

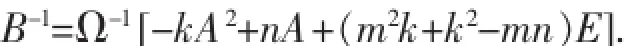
得证.

2 举例应用

例1已知n阶矩阵B＝A2+2A-E，其中n阶矩阵A满足A3＝3E，试验证B可逆并求其逆矩阵.

解这时k=3，m=2，n=-1，计算得d=n3+k2+ m3k-3mnk=50≠0，

由定理1可知矩阵B可逆，且

容易验算：

例2对于n阶矩阵B满B＝A2+2E，其中n阶矩阵A满足A3-A2-2E=0，试求B的逆矩阵.

解这里m=1，n=2，k=2，计算出Ω=m2k2+k3-2mnk+n2=8≠0，

由定理2可知矩阵B是可逆的，且

3 结论

定理1是针对矩阵A满足一个特殊三次方程，矩阵B是关于A的一般二次矩阵多项式，求B-1的问题；定理2则是针对矩阵A满足一般三次方程，矩阵B是关于A的一个特殊二次矩阵多项式，求B-1的问题，给出了这两类矩阵多项式求逆的具体方法，其它矩阵多项式求逆的问题也可以仿照此方法得以解决.

[1]北京大学数学系几何与代数教研室.高等代数[M].北京:高等教育出版社，1989.

[2]刘二根，谢霖铨.线性代数[M].南昌:江西高校出版社，2010.

[3]黄光鑫.一种关于求可逆矩阵的新方法[J].重庆师范学院学报，2002，19(1):35-36.

[4]王丽霞.逆矩阵的几种求法[J]．雁北师范学院学报，2007，23(2): 185-188.

[5]邵逸民.几类特殊矩阵的可逆性及其逆矩阵[J]．通化师范学院学报，2008(12):5-6.

[6]王美莲，何翠竹.一类特殊矩阵的逆矩阵的特点及求逆公式[J].忻州师范学院学报，2010，26(2):41-43.

[7]蒋加清.关于循环矩阵求逆的一种快速算法[J].吉林师范大学学报，2011(1):88-90.

[8]蒋加清.两类循环矩阵求逆的简便算法[J].曲阜师范大学学报，2011，37(4):44-48.

[9]邓义华.一类矩阵的逆矩阵和特征值问题[J]．洛阳师范学院学报，2005(2):33-34.

[10]邓义华.循环矩阵求逆的两个简便方法[J].云南师范大学学报，2005，25(5):1-2.

[11]杨明顺.三角矩阵求逆的一种方法[J].渭南师范学院学报，2003，18(5):12-13.

[12]张帆，王金林.一类中心对称矩阵反问题的最小二乘解[J]．江西理工大学学报，2012，33(1):86-89.

[13]陈芳，徐仲.求分块三对角矩阵和分块周期三对角矩阵逆矩阵的快速算法[J].数学的实践与认识，2005，32(12):183-187.

[14]余承依，陈跃辉.周期三对角矩阵逆的一种新算法[J].数学的实践与认识，2010，40(22):192-198.

[15]周梦，张玉俊.关于两个矩阵之和逆阵的讨论[J].大学数学，2011，27(5):149-151.

The inverse calculation of two types of matrix polynomials

LAI Xin-xing,XIAO Qing-lan
(Faculty of Science,Jiangxi University of Science and Technology,Ganzhou 341000,China)

The inverse calculation of matrix is an important problem in matrix theory,particularly the problem of the inversion of matrix polynomials.It is found that there are not only close ties but also special structures or forms between several kinds of special matrix and their inverse matrix.In the paper,inverse matrices solving methods of two classes of matrix polynomials are discussed to draw the formula of inverse matrices polynomials, and to put the results into real use.This study has certain important significance for solving relevant problems and the conclusion of it is also a good reference to further study of the inversion calculation of matrix polynomials．

matrix;matrix polynomial;inverse matrix

O151

A

2095-3046（2013）03-0090-03

2012-08-01

国家自然科学基金资助项目(61064006)；江西省教育厅青年科学基金资助项目(GJJ10155)；江西理工大学科研基金项目计划(jxxj12065)

赖新兴（1981-），男，讲师，主要从事代数等方面的研究，E-mail:doublexing@163.com．