车辆通过钢箱梁桥伸缩缝的振动响应及减振

吴延平，吴冬雁，谢旭，张鹤

（1.温州市城建设计院，浙江温州 325000；2.浙江大学土木工程系，杭州 310058）

桥梁伸缩缝处跳车已成为目前国内公路最为常见的道路病害之一。车辆在经过伸缩缝时所引起的冲击对桥梁及伸缩缝本身的安全性及使用寿命产生较大影响，刚度小、自重轻的钢桥，更容易引起此类问题。

车辆在经过桥梁结构时，会对桥梁产生多种动力效应，很多学者从理论与实测的角度进行了在一般路面下车桥耦合振动方面的大量研究[1―3]，考虑了包括行车速度、路面状况、车辆特性、桥梁类型等因素对车桥耦合振动的影响。由于桥梁伸缩缝的存在，更容易产生结构噪声、振动放大等问题。Ravshanovich K.A等[4]对车辆经过伸缩缝时噪声的产生机理进行了研究；Crocetti等[5]对modular型伸缩缝在车辆冲击荷载作用下的疲劳问题进行了研究；Steenbergen[6]研究了薄型伸缩缝在车辆荷载作用下的振动特性及伸缩缝的动力放大系数。但上述研究主要针对伸缩缝本身，而对车辆经过伸缩缝时对桥梁产生的冲击效应研究较少，邢世玲等[7]通过简单的模型研究了桥头凹陷深度对桥梁动力系数的影响；谢旭等[8]采用车桥耦合振动算法对伸缩缝跳车响应进行了数值模拟并通过实测进行对比分析。发现由于车辆经过伸缩缝时产生较大的冲击效应，对于一些桥梁特别是钢桥，有必要进行相应的减振设计。

本文以一座简支钢箱梁桥为对象，采用车桥耦合振动计算法，通过路面在伸缩缝位置的特殊处理来模拟伸缩缝的影响，得到车辆经过伸缩缝时的桥梁振动响应，并以此方法为基础进行伸缩缝冲击响应特性分析及降低桥梁对此冲击的响应，为桥梁由伸缩缝引起的振动计算方法和针对此类的减振设计提供参考。

1 桥梁概况及计算分析理论

1.1 桥梁概况及有限元模型

结构为单跨简支钢箱梁桥，跨径为65 m，宽度为9 m，如图1所示。上部结构采用两个分离式钢箱梁结构，每个箱梁高3.3 m，宽2.5 m，桥面板为正交异性钢板。在钢桥与预应力混凝土桥之间采用普通伸缩缝连接。

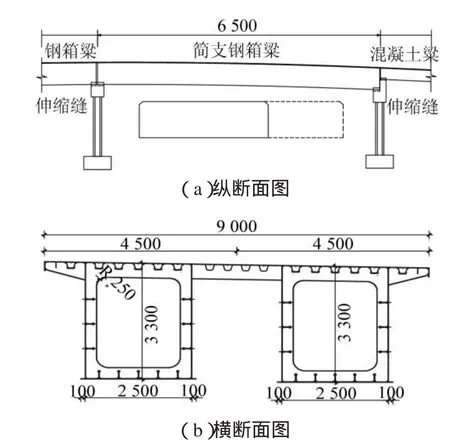
图1 桥梁结构图Fig.1 Sketch of bridge

本文近似采用三维杆系单元建立钢桥的梁格模型，其中每个小箱梁形成一根主梁，两个箱梁之间用横梁进行连接。整个模型共有190个梁单元和172个节点。

1.2 车桥耦合振动理论

车桥耦合振动计算系统由车辆、桥梁及车桥之间的路面接触三部分组成。本文计算采用4自由度的车辆模型，如图2所示。上部车体考虑上下竖向和转动振动，车辆弹簧下部考虑前后车轮的上下振动自由度。

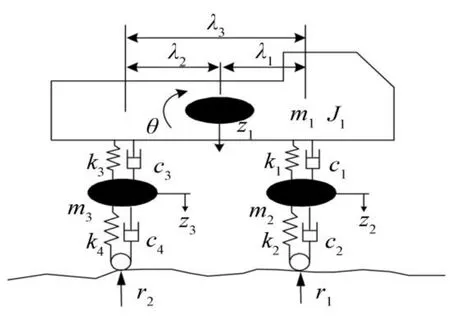
图2 4自由度车辆计算模型Fig.2 4-DOF model of vehicle

车桥之间的路面接触以ISO-8608中路面规定为基础，数值模拟本文中路面平整度。考虑到国内一般较新路面比标准中好，本文路面采用功率谱根据随机理论计算路面的凹凸不平整曲线，如图3所示。图中，r为从功率谱密度生成的路面不平整曲线样本，x为距离桥梁前端距离。

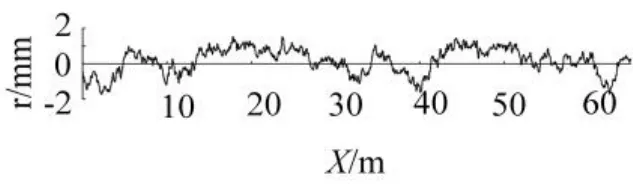
图3 路面凹凸不平样本Fig.3 Sample waves of road surface roughness

1.3 伸缩缝模拟及分析

为了考虑伸缩缝对车桥耦合振动计算的影响，通过改变在伸缩缝位置处的路面不平整度来考虑其影响。如图4所示为伸缩缝处的示意图。

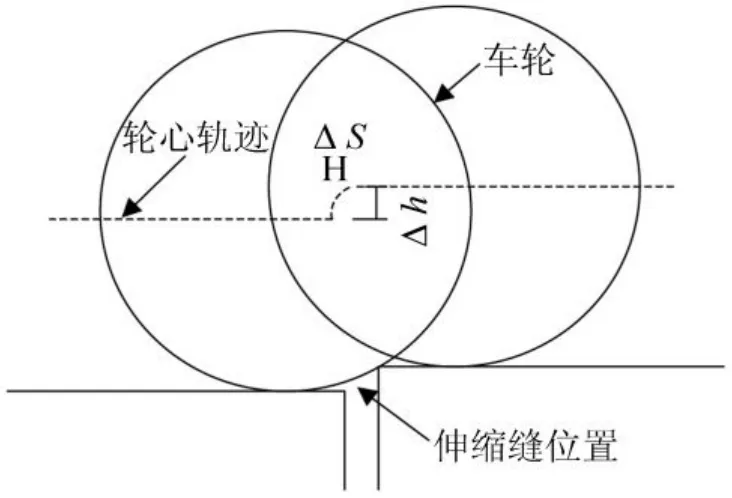
图4 伸缩缝示意图Fig.4 Sketch of expansion joint

由于路面条件对车辆振动荷载的影响主要体现在凹凸不平整r以及对应的变化率r，并且变化率与行车速度有关，随着行车速度的增大对应的路面变化率也增大。因此，在本文中在伸缩缝位置，对路面条件进行如下修改

式中v为通过伸缩缝时的行车速度；Δh为伸缩缝处前后的高差；ΔS为经过伸缩缝完成路面高差所经过的距离。

为了研究伸缩缝的冲击效应，本文根据实际情况，采用不同的Δh与ΔS对伸缩缝冲击响应进行参数分析。由于式（2）中是以Δh/ΔS为影响参数，故在分析中以Δh/ΔS和Δh为变化参数，以跨中位置时程加速度的峰值加速度apeak（如图5中的P点）为分析目标进行影响分析。

图5 考虑伸缩缝影响桥梁加速度时程Fig.5 Acceleration response of bridge considering the effect of expansion joint

图6为不同Δh与Δh/Δ15值下加速度峰值变化图，其中横轴表示Δh（单位mm）或Δh/ΔS（无量纲），纵轴为对应的加速度峰值，由图发现：1）（Δh/ΔS）的变化对冲击响应影响较大，特别在从1变化到5时，影响较显著。2）Δh的变化影响相对较小，当Δh/ΔS由0变化到2 cm时，apeak只从0.9 m/s2变化到1.2 m/s2；3）Δh的值确定根据桥梁伸缩缝两边的沉降差可确定，而Δh/ΔS值的确定最准确的方法为通过实测加速度峰值与数值计算进行比对确定。

1.4 小波变换理论

为了了解车辆在通过伸缩缝时对桥梁造成的冲击响应的振动特性，本文采用小波变换[9]对响应进行分析。由于伸缩缝的冲击效应使得结构的响应为非平稳过程，傅里叶变换只反映整个过程的频率特性，无法反映局部时间域内的振动特性，而小波变换能根据频率高低自动改变时间窗宽度，从而获得时域和频域的局部信号特性。

图 6 Δh/ΔS和Δh对加速度峰值影响图Fig.6 Peak acceleration at mid-span under different Δh/ΔSand Δh

小波变换中，所采用的小波函数有多种形式[10],如Morlet、Cauchy等。本文采用Morlet小波对信号进行分析，Morlet小波是高斯包络下单频率复正弦函数，其形式如下式（3）所示[10]

式中C表示重构时的归一化常数。

2 考虑伸缩缝影响的车桥耦合振动

2.1 振动响应时—频域分析

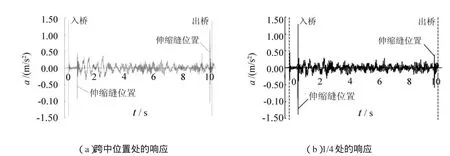
图7 考虑伸缩缝的加速度振动响应图Fig.7 Acceleration response at quarter and mid span considering the effect of expansion joint

如图7所示为Δh为8 mm，Δh/ΔS等于3，车速25 km/h时，在桥梁跨中及1/4跨位置的时程响应，由图可得：(1)车辆在进桥与出桥经过伸缩缝时，对跨中位置都造成了较大的冲击响应，其最大响应达到了1 m/s2左右，约为正常行驶最大响应的5倍，故由伸缩缝引起的冲击响应在设计中应予以重视；(2)在1/4跨位置处，在靠近伸缩缝测点处产生较大的影响，而在远离测点位置处的伸缩缝影响较小，由于1/4跨位置离进桥处的伸缩缝较近，其造成的最大响应达到了1.37 m/s2左右，而在车辆出桥时最大响应仅达到0.58 m/s2，说明由伸缩缝造成的冲击响应随着距离的增加消减得较快，而对伸缩缝位置附近的影响较突出。

如图8所示为利用Morlet小波对结构在上述图7中的时程响应进行小波分析的时—频域图，由图可得：(1)主频为2.4 Hz、10.7 Hz和22.0 Hz左右的振动贯穿于车辆经过桥梁结构的整个时间段，而这些频率接近结构的前3阶卓越频率，故车桥耦合振动响应主要以结构的前3阶振动为主；(2)当车辆经过伸缩缝时产生的冲击作用激发了桥梁的高频振动，其频率成分覆盖广，但高频振动随时间迅速衰减。

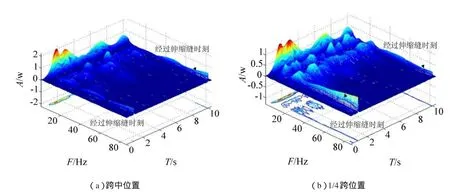
图8 小波变换时—频域图Fig.8 Wavelet transform of acceleration response

2.2 冲击振动影响因素分析

影响车辆伸缩缝振动响应的因素主要来自移动车辆和伸缩缝处路面特性两个方面，伸缩缝特性对其的影响在1.3中已分析，下面就移动车辆对其的影响进行分析。而移动车辆的影响因素主要为车速和车辆类别，其中车辆类别主要体现在车重的不同。

如图9所示为车速10 km/h、40 km/h和70 km/h下的加速度时程响应图，由图可得：伸缩缝冲击响应随着车速的增加而增加，这是由于在路面变化率式（2）中车速也产生影响，但是当车速增加到一定程度时，其对经过伸缩缝时的冲击响应影响有限，而主要表现在影响整个车桥耦合振动过程，如图中当速度由10 km/h增加到40 km/h时冲击加速度峰值由0.47 m/s2提高到0.84 m/s2，而速度为70 km/h时，其值为0.95 m/s2，增加幅度较小。

如图10所示为相同车速下，车重分别为10 t、20 t和40 t的加速度时程图，由图可得：不同车重对伸缩缝的冲击作用有显著差别，随着车重的增加，冲击作用明显增加，当车重由10 t增加到40 t时，加速度冲击峰值相差达3.5倍。因此，在桥梁运营中，需充分考虑超重车辆经过伸缩缝时形成的冲击效应对结构的健康使用产生的影响。

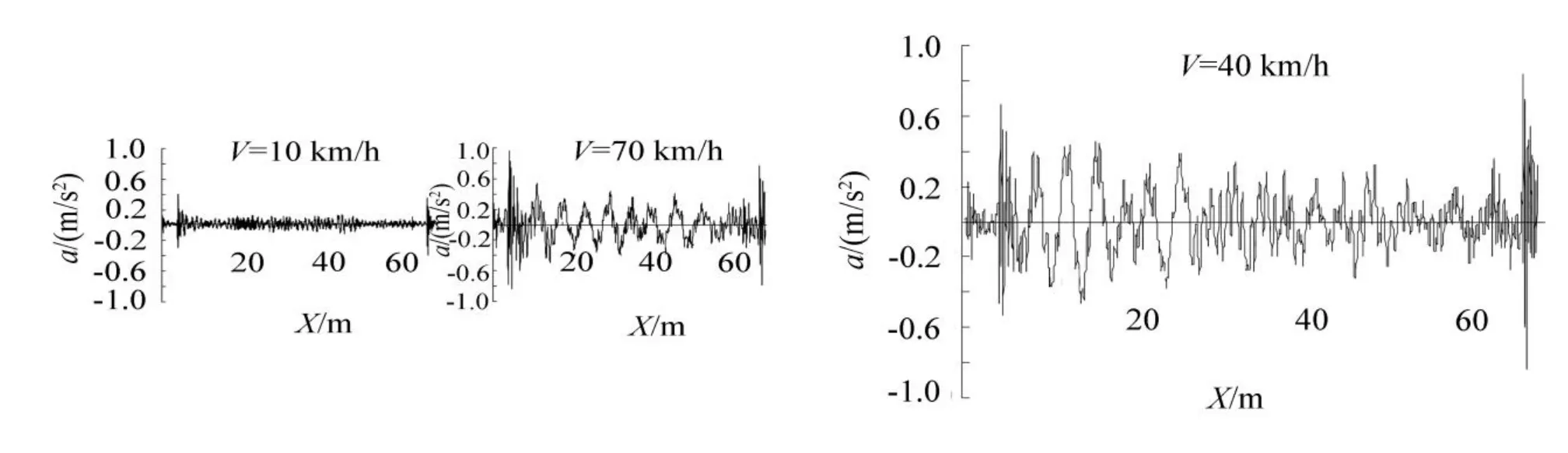
图9 跨中位置不同车速下的加速度时程图Fig.9 Acceleration response at mid span under different vehicle speeds

图10 不同车重下的加速度时程图Fig.10 Acceleration response at mid span under different vehicle weights

3 减振方法分析

3.1 减振方法

桥梁结构的减振方法多种多样，在实际应用中比较多采用的是质量阻尼器法（TMD）等，另外还有改变边界条件，如使用橡胶弹性支座，以及加强结构刚度，如梁端混凝土填筑法等。

因为由伸缩缝引起的冲击效应多集中在高频区域，而TMD法主要控制结构的低阶频率，故在降低伸缩缝冲击效应中效果不理想。而橡胶弹性支座主要通过橡胶变形达到控制结构位移的目的，而伸缩缝冲击作用对结构位移影响较小，故其减振效果也不显著。在梁端混凝土填筑法中，对离梁端部一定范围内的钢箱梁内填筑素混凝土增加局部的结构刚度来达到减振的目的。

以梁端混凝土填筑减振方法为对象，分析其在伸缩缝冲击作用中的减振效果，并且分析填筑长度对减振效果的影响。

3.2 梁端混凝土填筑法减振分析

如图11所示为梁端填筑不同长度素混凝土后在跨中位置的峰值加速度比较图，由图可得：1）梁端填筑混凝土能有效的减少车辆经过伸缩缝时的冲击效应，当梁端填筑6 m时，其峰值加速度由原来的1.13 m/s2降到了0.38 m/s2，与正常的车桥耦合振动响应相近，表明此方法对由伸缩缝引起的冲击振动有较好的减振效果；2）素混凝土填筑长度的不同对减振效果有一定的影响，但当填筑达到一定长度时，增大填筑长度对减振效果的提高不是很显著，当填筑长度从0 m增加到4 m时，其峰值从1.13 m/s2降到0.44 m/s2，当4 m增加到8 m时，从0.44 m/s2降到0.34 m/s2，因而对于文中桥梁填筑6 m左右就可基本达到抑制伸缩缝引起的冲击振动的目的。

图11 梁端填筑不同长度减振效果比较图Fig.11 Effect of vibration control under different lengths of concrete filled

4 结语

通过数值模拟车辆经过一简支钢箱梁桥伸缩缝时产生的冲击响应计算分析，得到了如下结论：

(1)改变伸缩缝位置处的路面粗糙度特性的车桥耦合振动计算方法能在一定程度上模拟车辆经过伸缩缝时产生的振动效应，但计算中的个别参数的精确取值最好通过实测确定；

(2)车辆经过伸缩缝所形成的冲击可使结构的加速度响应增大为正常车桥耦合振动响应的5～6倍，并且以高频振动为主，随着时间与距离的增加而快速衰减；

(3)伸缩缝处的特性（如高差等）、车速与车重对车辆经过伸缩缝产生的冲击响应都有较显著的影响；

(4)梁端混凝土填筑法能有效减少此类振动所产生的冲击效应，其减振效果与填筑的长度有关，但当填筑达到一定长度时则不会增加减振效果。因此，设计中需取合理填筑长度。

[1]Kim C W,Kawatani M,Kim K B.Three dimensional dynamic analysisforbridge-vehicle interaction with roadway roughness[J].Computers&Structures,2005,83(19-20):1627-1645.

[2]Chang T.P.,Liu M.F.,O H.W.Vibration analysis of a uniform beam traversed by a moving vehicle with random mass and random velocity[J].Structural Engineering and Mechanics,2009,31(6):737-749.

[3]Xu Hongan,Li Wen L.Dynamic behavior of multi-span bridges under moving loads with focusing on the effect of the coupling conditions between spans[J].Journal of SoundAnd Vibration,2008,312(4-5):736-753.

[4] Ravshanovich K.A.,Yamaguchi H.,Matsumoto Y.Mechanism of noise generation from a modular expansion joint under vehicle passage[J].Engineering Structures,2007,29(9):2206-2218.

[5]Crocetti R,Edlund B.Fatigue performance of modular bridge expansion joints[J].Journal of Performance of Constructed Facilities,2003,17(4):167-176.

[6]Steenbergen M.Dynamic response of expansion joints to traffic loading[J].Engineering Structures,2004,26:1677-1690.

[7]邢世玲，陈彦江，孙航.“桥头跳车”对桥梁动力响应的影响分析[J].中南公路工程，2007，32(1)：119-121.

[8]谢旭，吴冬雁，王建峰，张世琦，周永杰.伸缩缝车辆冲击引起的钢箱梁桥振动特性[J].浙江大学学报（工学版），2009，43(10)：1923-1930.

[9] Daubechies I.The Wavelet transform,time-frequency localization and signal analysis[J].IEEE Transactions on Information Theory,1990,(36)5:961-1005.

[10]Le TP,Argoul P.Continuous wavelet transform for modal identification using free decay response[J].Journal of Sound and Vibration,2004,277(1-2):73-100.