金属圆柱壳参数变化对缓冲吸能的影响

戴向胜，马建敏

（复旦大学力学与工程科学系，上海 200433）

金属圆柱壳能够以稳定的塑性变形模式吸收大量的能量，是最有效的缓冲吸能结构之一，文献1对单个圆柱壳在轴对称冲击载荷作用下所涉及的问题作了很好的总结；文献2运用实验以及有限元方法对单个圆柱壳进行了研究，得到圆柱壳在低速和高速冲击下的平均载荷以及瞬时载荷位移历程曲线；文献3通过试验方法研究了薄壁铝管塑性变形缓冲器在准静态作用下的吸能特性，对各种缓冲器的缓冲性能进行综合评价，给出了三类缓冲器缓冲性能的评价方法。本文在单个圆柱壳缓冲吸能研究的基础上，研究产生轴对称叠缩而且受力均匀情况下圆柱壳的材料、厚度、半径以及数量的变化对缓冲效果的影响。

1 圆柱壳缓冲吸能计算

V0建立一个包括冲击块与圆柱壳的系统，假设质量是M的冲击块在接触圆柱壳时的初始冲击速度是V0，在冲击过程中冲击块的垂直位移是δ时冲击块的速度是Vδ，设零势能面在圆柱壳的底面，圆柱壳的长度是L、厚度是h、半径是R。

Vδδ圆柱壳在冲击过程中的缓冲效果主要是根据冲击块的速度位移曲线、圆柱壳的平均载荷以及圆柱壳的瞬时载荷位移曲线进行评价。冲击块的速度位移曲线可以得到圆柱壳在给定的冲击块速度下的完成缓冲系能过程所需要的叠缩位移；平均载荷以及瞬时载荷就是圆柱壳作用在冲击块上的作用力，平均载荷以及瞬时载荷曲线波动幅度越小、数值越小说明缓冲效果越好。

ESδ在冲击块的冲击作用下圆柱壳会产生塑性变形叠缩从而相应的引起已经变形叠缩部分有机械能，该部分的机械能与圆柱壳在冲击过程中所产生的塑性变形能相比较数值很小，所以本文忽略。只考虑冲击块的机械能和圆柱壳的塑性变形能，其中圆柱壳的塑性变形能ESδ可以根据文献4中提出轴对称Singace模式（图1）角度增量叠缩法进行计算。

把整个内翻阶段塑性叠缩变形过程根据角度增量Δα分成N个叠缩，整个塑性变形能是所有叠缩的塑性变形能之和，塑性变形能包括弯曲变形能和伸缩变形能。

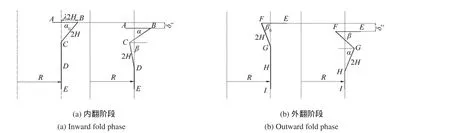
图1 Singace叠缩模式Fig.1 Singace fold model

弯曲变形能包括在叠缩过程中的三个塑性铰B、C、D(对应的j=1、2、3)因为角度变化而产生的塑性变形能计算公式如下式中是每个塑性铰到轴线的距离

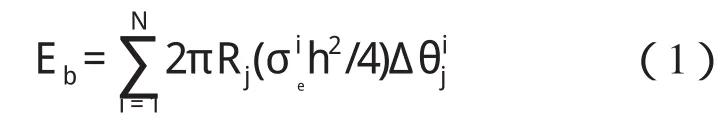
Δ是是第i个叠缩中材料的等效应力，是第i个叠缩中塑性铰的转动角度。

伸缩变形能是圆柱壳在周长方向上有伸缩变形而产生的塑性变形能计算公式如下

在公式（1）中的应用Johnson Cook本构方程进行计算

T为材料温度、Tr为室温、Tm为材料的熔点温度

ESδ根据公式（1）（2）圆柱壳的塑性变形能是

E0在初始时刻系统的总能量是冲击块的动能及势能之和

ESδEδδEMδ在冲击接触过程中冲击块的垂直位移是时，系统总能量包括冲击块的机械能以及圆柱壳的塑性变形能

所以系统总能量是

根据冲击块以及圆柱壳所组成的系统能量守恒有

根据公式（7）、（8）可以得到冲击块的速度与位移之间的关系

Fm冲击过程中圆柱壳的平均载荷可以用圆柱壳在叠缩过程中所吸收的塑性变形能和圆柱壳叠缩的垂直位移之比得到

ESδ式中是圆柱壳在叠缩过程中所吸收的塑性变形能，δ是圆柱壳叠缩的垂直位移。

冲击过程中的瞬时载荷可用第i个叠缩中圆柱壳的塑性变形能变化量和叠缩垂直位移的变化量之比得到第i个叠缩中瞬时载荷

Δδ(i) ΔES(i)是第i个叠缩中圆柱壳的塑性变形能变化量，是圆柱壳叠缩垂直位移的变化量。

2 计算分析

根据公式（9）可以计算得到冲击块的速度位移曲线、根据公式（10）可以计算得到圆柱壳的平均载荷位移曲线，根据公式（11）可以计算得到圆柱壳的瞬时载荷位移曲线。其中在计算圆柱壳的塑性变形能时需要用到材料的Johnson Cook本构参数以及几何参数如下

875J/(K g·K )1）铝 合 金 2 024 Al-T 351，其Johnson Cook本构参数是：A=265 Mpa、B=426 Mpa、n=0.34、C=0.015、m=1；比热容

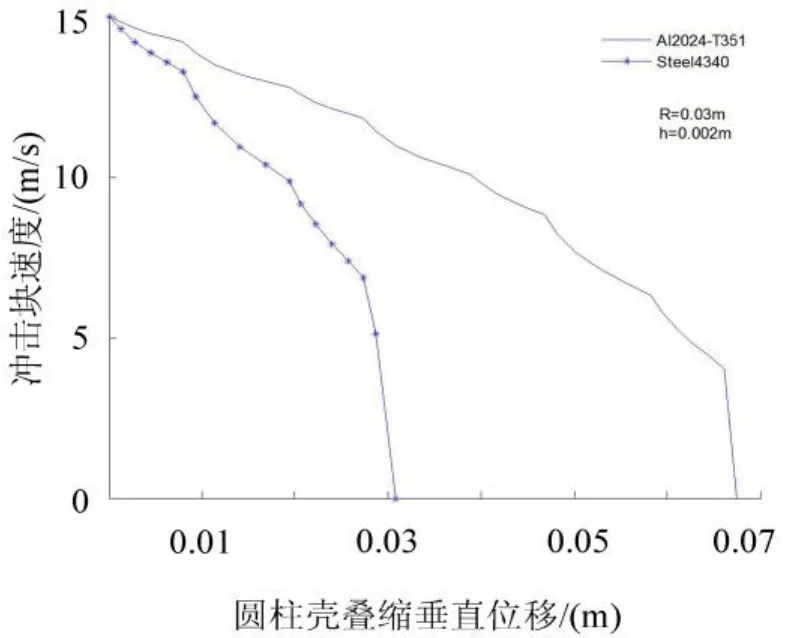
图2 不同材料下冲击块的速度位移曲线Fig.2 Speed displacement curve of impact object with different material

2770k g/m3密度；溶化温度775 K

78 30k g/m31793J/(k g·K)2)钢 4 340 Steel，其Johnson Cook本构参数是：A=792 Mpa、B=510 Mpa、n=0.26、C=0.014、m=1.03；比热容 1 793 J/(kg·K)；密度7830 kg/m3；溶化温度480 K；

3）几何参数是：半径R=30 mm、壁厚h=2 mm、长度0.3 m、偏心率λ=0.5，冲击块质量是25 kg，冲击速度是15 m/s。

计算结果如下

（1）圆柱壳采用不同材料

当材料是4340 Steel时的圆柱壳平均载荷位移曲线以及瞬时载荷位移曲线比2024Al-T 351数值更大，因此采用不同材料对圆柱壳缓冲效果有着显著的影响。

（2）厚度变化分析

图3 不同材料下圆柱壳平均载荷位移曲线Fig.3 Mean load displacement curve of shell with different material

图4 不同材料下的圆柱壳瞬时载荷位移曲线Fig.4 Instantaneous load displacement curve of shell with different material

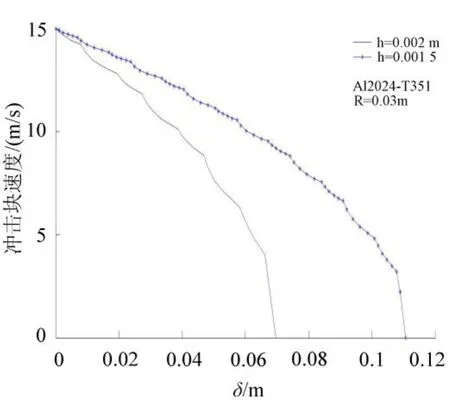
图5 不同厚度下的冲击块速度位移曲线Fig.5 Speed displacement curve of impact object with different thickness

图6 不同厚度下的圆柱壳平均载荷位移曲线Fig.6 Mean load displacement curve of shell with different thickness

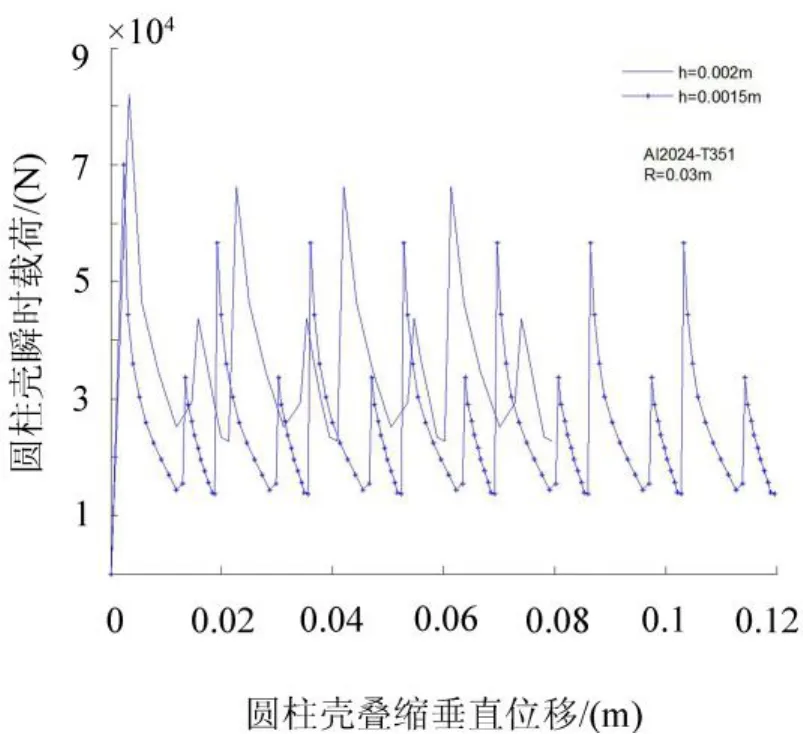
图7 不同厚度下的圆柱壳瞬时载荷位移曲线Fig.7 Iinstantaneous load displacement curve of shell with different thickness

图8 不同半径下的冲击块速度位移曲线Fig.8 Speed displacement curve of impact object with different radius

图9 不同半径下的圆柱壳平均载荷位移曲线Fig.9 Mean load displacement curve of shell with different radius

图10 不同半径下的圆柱壳瞬时载荷位移曲线Fig.10 Instantaneous load displacement curve of shell with different radius

图11 不同数量下的冲击块速度位移历程曲线Fig.11 Speed displacement curve of impact object with different number

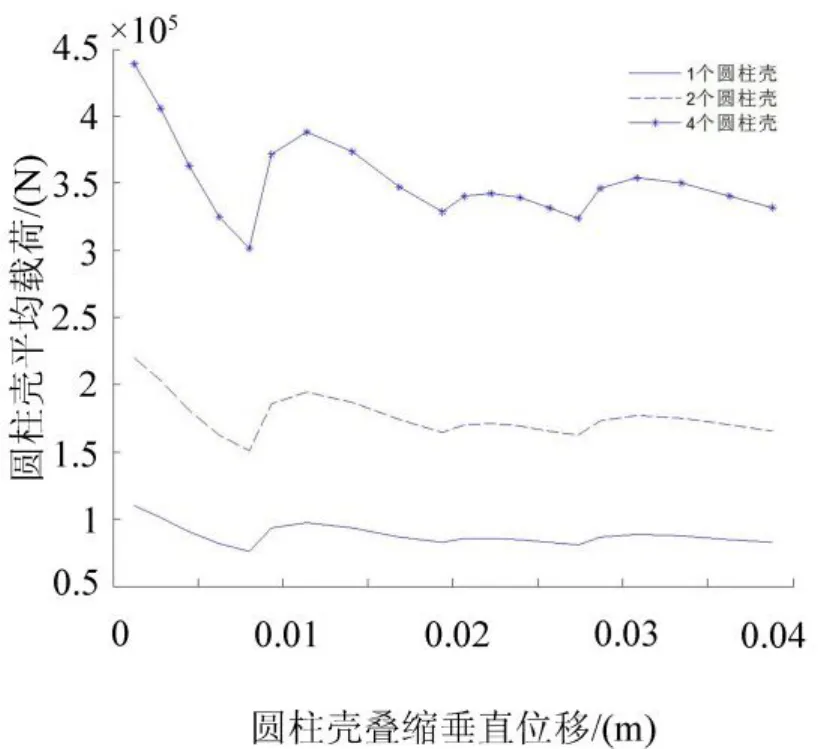
图12 不同数量下的圆柱壳平均载荷位移曲线Fig.12 Mean load displacement curve of shell with different number

图13 不同数量下的圆柱壳瞬时载荷位移曲线Fig.13 Instantaneous load displacement curve of shell with different number

从图5中可以得到，在相同的冲击速度下，随着厚度的增大圆柱壳完成冲击缓冲作用所要的叠缩垂直位移减少；从图6、图7中可以得到随着厚度的增大圆柱壳平均载荷位移曲线以及瞬时载荷位移曲线的幅值增大。

（3）半径参数变化分析

从图8中可以得到，在相同的冲击速度下，随着半径的增大圆柱壳完成冲击缓冲作用所要的叠缩垂直位移减少；从图9、图10中可以得到随着半径的增大圆柱壳平均载荷位移曲线以及瞬时载荷位移曲线的幅值增大。

（4）数量变化分析

从图11、图12以及图13中可以得到，随着数量的增加圆柱壳完成冲击缓冲作用所要的叠缩垂直位移减少；单个圆柱壳的平均载荷位移曲线以及瞬时载荷位移曲线没有变化；增加圆柱壳数量增加了总的圆柱壳的平均载荷位移以及瞬时载荷。

因为冲击块与圆柱壳之间是作用力与反作用力的关系，冲击块的平均载荷以及瞬时载荷位移历程曲线与单个圆柱壳平均载荷以及瞬时载荷位移历程曲线有着成倍关系。

3 结语

改变圆柱壳的数量、半径、厚度以及材料都能相应的改变冲击缓冲作用所要的叠缩垂直位移；圆柱壳的平均载荷以及瞬时载荷位移历程曲线主要取决于圆柱壳的材料、半径以及厚度，而与数量没有关系；在圆柱壳缓冲设计时可以通过改变圆柱壳的数量、材料、半径以及厚度确定合理的叠缩垂直位移、圆柱壳及冲击块平均载荷以及瞬时载荷位移历程曲线，实现预定的缓冲效果。

[1]Jones N.Recent studies in the dynamic plastic behavior structures[J].Mech.Review,1989(42):95-115.

[2] Nader Abedrabboa,ets.Crash response of advanced high-strength steel tubes:Experiment and model[J].International Journal of Impact Engineering,36(2009)1044-1057.

[3]罗昌杰.薄壁金属管塑性变形缓冲器吸能特性的试验研究[J].振动与冲击，2010，(29)4.

[4]戴向胜，马建敏.冲击载荷作用下金属圆柱壳能量吸收研究[J].振动与冲击，2012，31(6)：100-103.