平缝机刺布挑线机构的动力学优化

刘亚辉，杨华，周长江

(1.湖南大学车身先进设计制造国家重点实验室，长沙 410082；2.湖南大学机械与运载工程学院，长沙 410082)

在高速运转下，周期性的激励使平缝机的振动加大，动态性能恶化，缩短了机械的使用寿命，破坏了工作坏境，不利于工人的身心健康。因此，有效降低工业平缝机的振动噪声，改善其动态性能，具有重要意义。

平缝机噪声主要是由机构运动过程中所产生的不平衡力造成的，很多文献对此进行了研究。文献[1]发现机构的不平衡力和运动产生的激励及其在轴上分布的不平衡，是高速平缝机产生振动和噪声的主要来源。同时，国内外学者就机构运动过程中的不平衡，在相关领域作了大量改进工作。文献[2]通过在连杆上添加平衡配重，得到了摆动力矩均方根最小的最优配重方案。文献[3]针对曲柄滑块机构中的部分平衡，考虑了最大惯性力和惯性力矩的平均值两项优化指标，选择最佳平衡量进行机构平衡。文献[4]通过附加杆组和附加齿轮对的方法对机构振动力和振动力矩进行平衡。文献[5]通过添加对称杆组的办法对曲柄滑块部分进行平衡。文献[6]以工业平缝机减振降噪为背景，基于复数矢量法和机构环路方程对一类平面六杆机构的惯性力进行分析推导，以谐波分量的均方根为目标函数，进行机构的优化设计。文献[7]和文献[8]以振动力和振动力矩的组合构造优化目标函数，选取合理的权重系数，对缝纫机刺布挑线机构的六杆机构的构件质量、质心位置等参数进行了动平衡的优化设计，其中文献[8]还做了整机的优化平衡。文献[9]以振动力和振动力矩的组合在一个周期内积分的平均为优化目标，通过在针杆曲柄和挑线杆连杆处添加配重，对刺布挑线机构进行了动平衡的优化。

工业平缝机刺布挑线机构是一个六杆机构，理论上需要添加三个配重方可完全平衡。受空间和质量限制，适合基于部分平衡理论对针杆曲柄进行平衡优化。以某型高速平缝机为研究对象，在UG中建立刺布挑线机构的几何模型，导入ADAMS中进行分析计算。以针杆曲柄在一个运动循环中最大惯性力最小为优化目标，对机构的惯性力进行动平衡的优化。

1 刺布挑线机构模型建立及分析流程

刺布挑线机构是工业平缝机的重要组成机构，位置如图1所示。

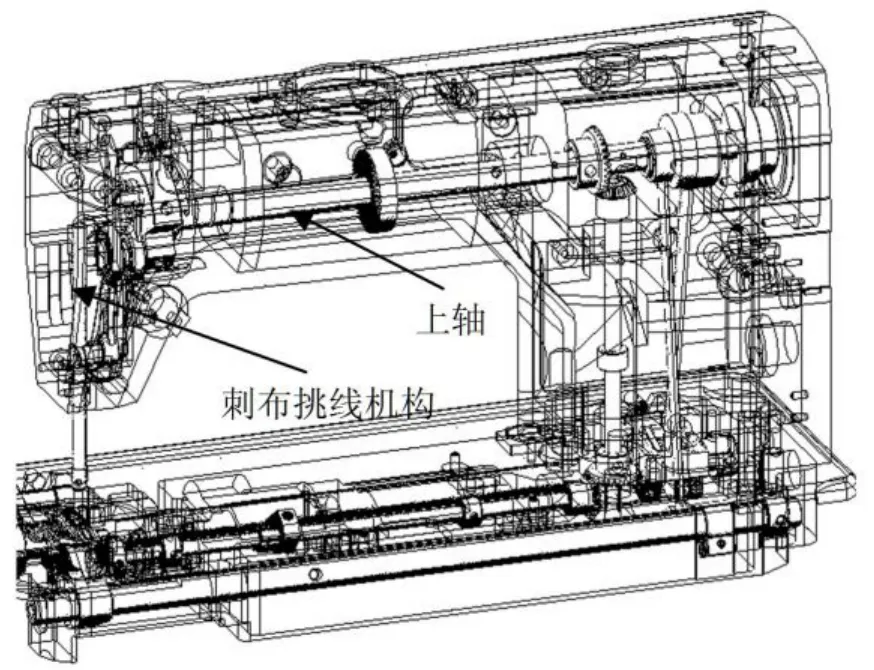
图1 刺布挑线机构在整机中位置示意图Fig.1 Location of puncturing and stirring mechanism in sewing machine

在UG中建立各部件的实体模型并完成模型装配，对机构模型进行预处理，检查装配模型的干涉，对模型进行适当简化和修改。以Parasolid格式导入ADAMS中，以各构件的材料属性和实际运动为基础简化模型，添加适当的约束（如图2）。针杆曲柄与机架之间（A处）添加旋转副，挑线连杆与机架之间（B处）添加圆柱副，挑线杆与挑线连杆之间（C处）添加球副，针杆曲柄与挑线杆、挑线杆与针杆连杆之间（D处）添加两个旋转副，E处和F处分别为圆柱副，在A处旋转副上添加4 000 r/min的驱动，从而完成平缝机刺布挑线机构装配模型到动力学模型的转化。

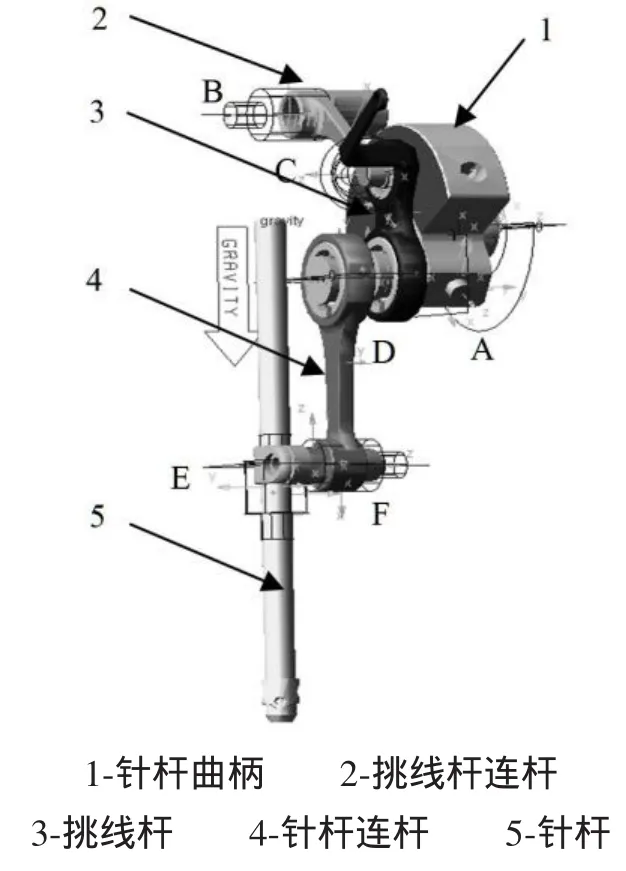
图2 刺布挑线机构动力学模型Fig.2 Dynamic model of puncturing and stirring mechanism

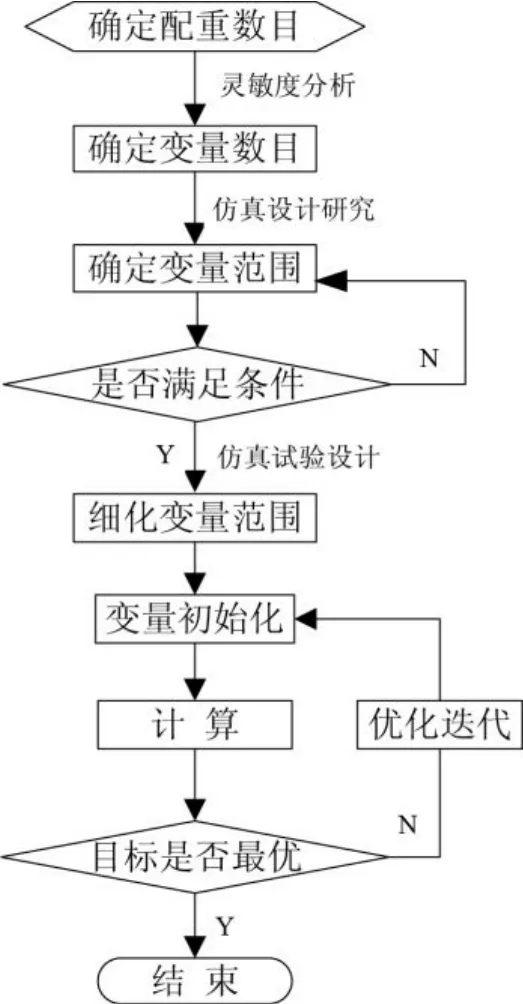
图3 机构动平衡仿真计算流程图Fig.3 Dynamic balance process of mechanism basing on simulation

分析流程如图3所示，首先，通过ADAMS/View提供的参数分析方法初步确定每个变量的大概范围，观察样机主要性能的变化规律及各变量对目标函数的影响。进行灵敏度分析，灵敏度值表示每单位变量对目标的影响，以灵敏度较大的变量作为优化变量。利用仿真试验设计来确定各变量之间的大致关系。最后优化设计，选择合适的优化算法、收敛公差等进行优化计算。

2 针杆曲柄的优化

2.1 优化目标及其数学模型

机构在运转过程中，惯性力和惯性力矩是随时间作周期变化的。根据机械振动理论，对于一个确定的系统，振动的大小是由激振力的幅值决定的。对单个机构进行优化平衡时，可以以一个运动循环中，最大惯性力最小作为优化目标。选择针杆曲柄转动副处惯性力为研究对象，即

等式右边表示一个运动循环中最大惯性力；θ表示曲柄转角；X表示设计变量。对机构平衡的实质是在机构的某些构件上附加配重，改变质量的分布状况。刺布挑线机构共有5个运动构件，受机构的结构尺寸、加工工艺、运动空间等限制，在此只对构件1（针杆曲柄）进行优化。确定一个配重需要四个量，配重在坐标系中的位置坐标和配重质量作为设计变量，即

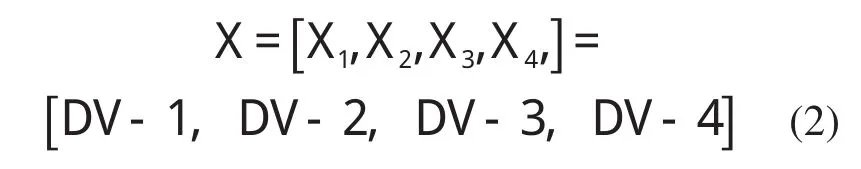
DV_1，DV_2，DV_3和DV_4分别代表曲柄连杆机构的质心位置X、Y及Z三个方向的坐标和针杆曲柄的质量。为得到可行的优化方案，对设计变量变化范围加以限制，即令X1≤X≤Xh，其中X1为X下限值，Xh为X的上限值。

机构振动力矩并不是随其振动力矩的减小而减小，某些情况下振动力矩反而会增加，使振动更加剧烈[10]。因此，考虑到平缝机的整体动态性能，在降低惯性力的同时，尚需对惯性力矩加以限制，即应使机构在一个运动循环中，对主轴惯性力矩之和的最大值小于给定惯性力矩值A，A为平衡前的一个运动循环中，机构对主轴的最大惯性力矩。则有

综上所述，刺布挑线机构的优化数学模型可表达为

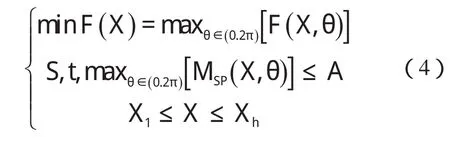
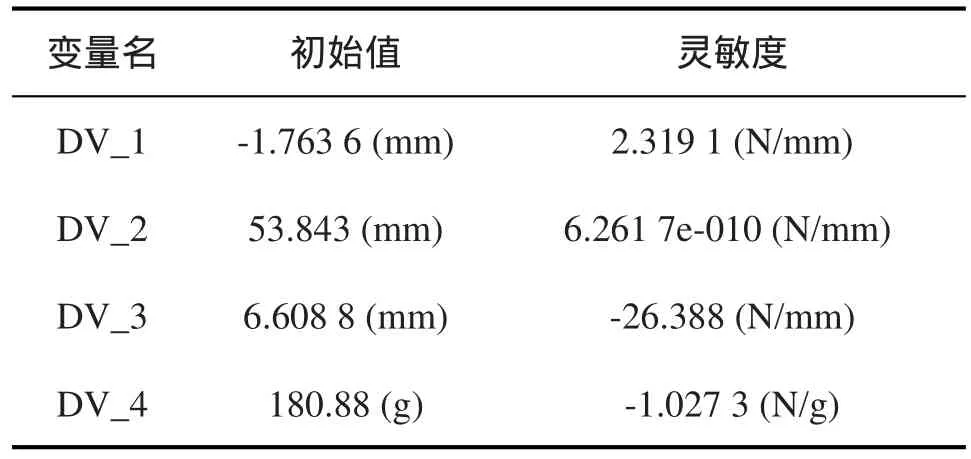
表1 各变量对针杆曲柄处惯性力的影响Tab.1 The impact of each variable on inertia force of the needle bar crank

利用ADAMS对影响针杆曲柄处惯性力的因素进行优化。各变量对针杆曲柄处惯性力的影响见表1。其中DV_2对针杆曲柄处惯性力影响甚微，实际优化时可以不予考虑。

2.2 优化结果分析

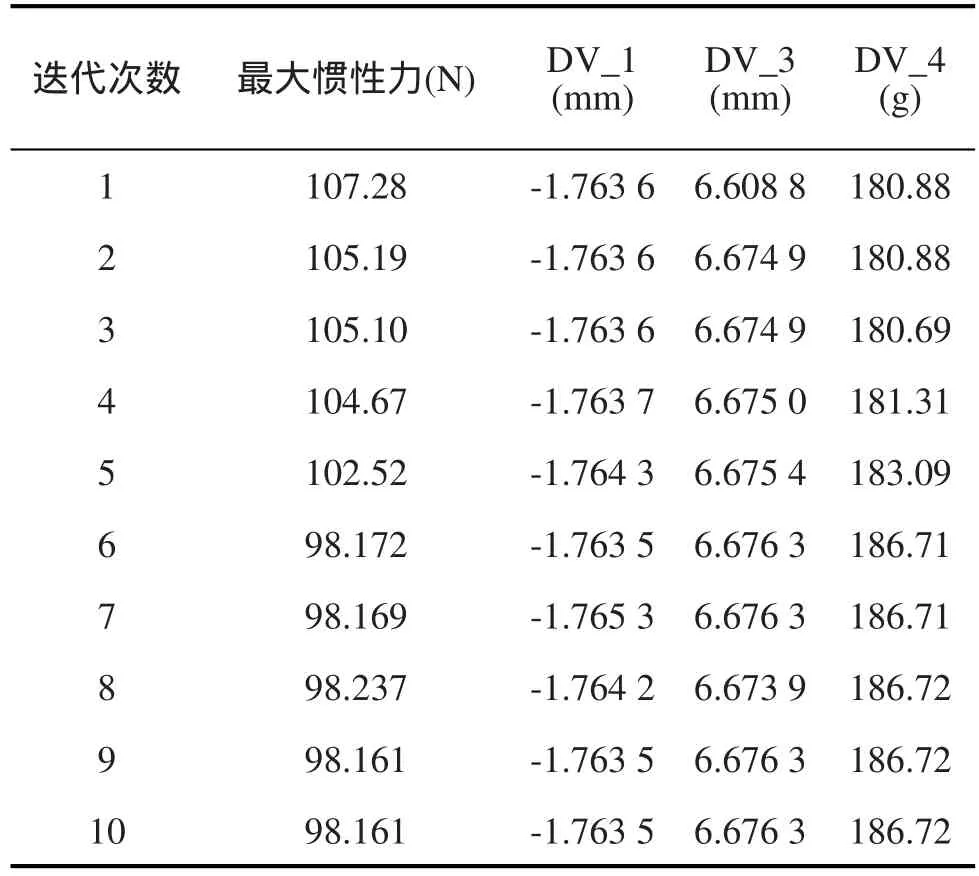
表2 优化迭代过程Tab.2 Iterative process of optimization

表2显示优化迭代过程中不同迭代次数下对应最大惯性力和变量大小。表2显示，在第9次迭代后最大惯性力达到最优。

图4描述了优化前后惯性力在一个周期内随时间变化情况。优化前惯性力在t=0.008 5 s处取得最大值为107.284 4 N，优化后惯性力在t=0.008 5 s处取得最大值为98.160 9 N。可见，优化后惯性力最大值明显优于优化前，优化空间为8.50%。

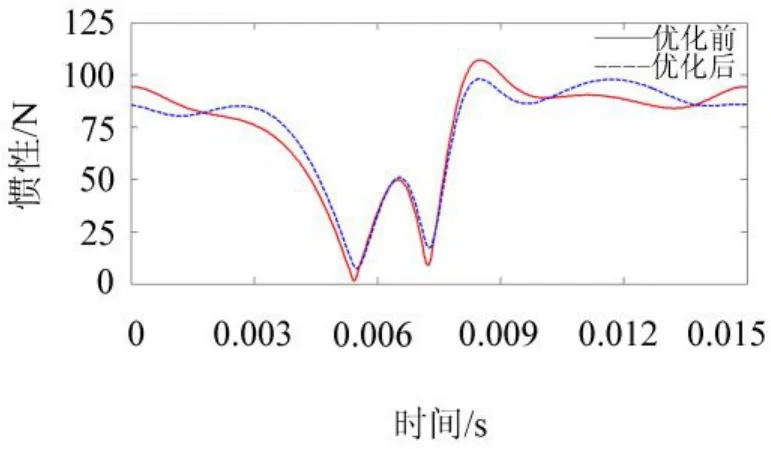
图4 优化前后惯性力合力比较Fig.4 Contrast of the sum of the inertia force before and after optimization

3 试验对比

在一批产品中随机抽取两台平缝机，按标准《QB/T 1177-2007工业缝纫机噪声级的测试方法》，分别测试其平衡前后的噪声、标准点(A点)加速度及麦克风输出电压。加速度传感器布置图如图5所示，噪声测试布局图如图6所示，结果如表3所示，麦克风输出电压PSD的频域图如图7和图8所示。

图5 加速度传感器布置图Fig.5 Layout diagram of acceleration sensor

表3 平衡前后试验结果对比Tab.3 Contrast of test results before and after balance

图6 平缝机噪声测试布局图Fig.6 Layout diagram of noise experiment of sewing machine

图7 平衡前电压PSD频域图Fig.7 Frequency domain chart of voltage PSD before balance

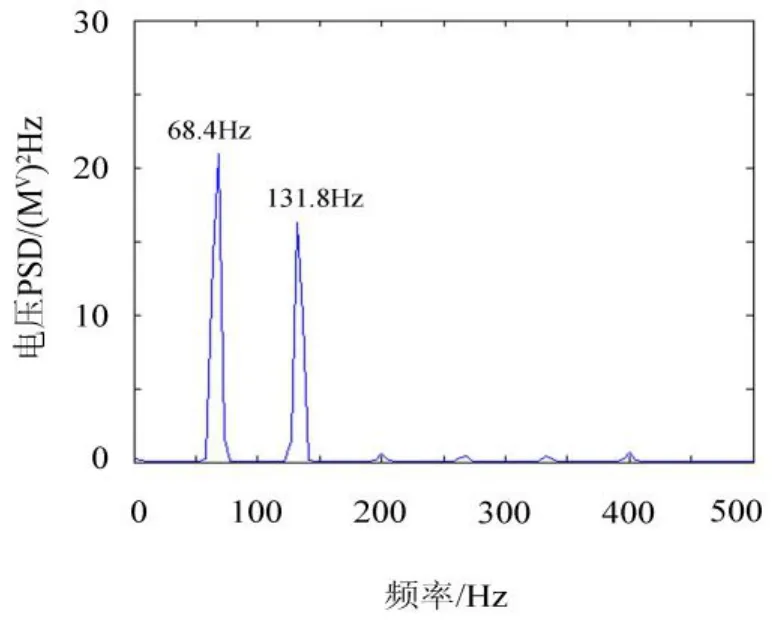
图8 平衡后电压频谱图Fig.8 Frequency domain chart of voltage PSD after balance

由表3可知，优化平衡后，两台样机噪声均有所降低，1号样机降低1.1 dB，二号样机降低1.0 dB；测试标准点三个方向的加速度相比优化前均有所减小，其中y方向变化较小，为5.9%～10.87%，x和z方向变化比较明显，分别为19.12%～20.18%和21.37%～23.79%；电压PSD频谱图中有两个波峰，频率为68.4 Hz和131.8 Hz，分别对应上轴（4 000 r/min）及下轴（8000 r/min）的旋转频率，图7和图8对比可知，平衡前后，两峰值对应的电压PSD值均有所降低。

4 结语

(1)优化针杆曲柄对噪声的控制有一定的效果，优化后噪声降低了约1 dB；

(2)在受诸多约束的情况下，部分平衡法能较好地应用于解决如高速平缝机等复杂机械系统的动平衡分析；

(3)基于ADAMS的数值分析法与样机试验方法相结合，对平缝机的重要机构进行动态优化设计，可以获得比较可信的结果。

[1]刘其洪，邵汝椿，林颖，等.高速工业平缝机减振降噪试验研究[J].华南理工大学学报（自然科学版），1996，24(8).

[2]V.Arakelian,M.Dahan.Partial shaking moment balancing of fully force balanced linkages[J].Mechanismand Machine Theory,2001(36):1241-1252.

[3]王学武，张青，郭为忠.曲柄滑块机构惯性力优化平衡的新方法[J].机械科学与技术，2006，25(6)：687-688.

[4]Arakelian V H,Smith M R.Shaking force and shaking mo ment balancing of mechanisms:a historical review with new examples[J].Journal of Mechanical Design,2005,127(2):334-339.

[5]Arakelian V H.Shaking moment cancellation of self-balanced slider-crank mechanical systems by means of optimum mass redistribution[J].Mechanics Research Communica-tions,2006,(33):846-850.

[6]王永泉，陈花玲.机构动态优化在工业平缝机减振中的应用[J].机械科学与技术，2005，24(8)：947-949.

[7]李鹏飞，陈卫宁，朱强，等.高速工业平缝机机构动平衡优化设计[J].机械科学与技术，2011，30(3).

[8]张雄，傅祥志.高速平缝机的振动及噪声控制[J].华中理工大学学报，1993，21(2).

[9]王玉喜.无油润滑工业平缝机机构的设计与分析[D].哈尔滨：哈尔滨工业大学，2007：31-47.

[10]Lowen G G,Tenpper F R,Berkof R S.The quantitive infulance of complete force balancing on the forces and moments of certain families of four-bar linkages[J]Mechanism and Machine Theor y,1974(9):299-323.