运行工况传递路径分析识别车内声源

李传兵，王彬星，李宏成，王月琳，郑四发

（1.重庆长安汽车股份有限公司，重庆 400023；2.清华大学汽车安全与节能国家重点实验室，北京 100084）

汽车作为一个复杂系统，受多种振动噪声源的激励。动力传动系统的振动噪声是车内主要噪声源之一。准确确定各声源的位置及对车内噪声的贡献，是制定合理的降噪方案的基础。传递路径分析[1](Transfer PathAnalysis，TPA)的目的不仅在于预测系统响应，更重要的是通过估计噪声源和传递路径的贡献率，找出对响应影响较大的关键噪声源和传递路径，从而可以有的放矢地改进设计[2―4]。传统传递路径分析方法在应用中主要存在如下不足[5]：单个传递路径测试时由于边界条件的改变带来测量误差；采用间接方法测量力激励和声激励带来测量误差；测量时外加声源及振源激励的过程复杂，工作量大。

运行工况传递路径分析(Operational Transfer Path Analysis,OTPA)[6]是对传统路径分析的改进。OTPA用系统工作时激励参考信号表征原有的载荷激励信号。这样，只需在激励部分的参考点和声压响应点布置传感器，传递函数的计算只需考虑激励参考点和声压响应点之间的传递特性。采用OTPA方法对某乘用车车内噪声源贡献率进行了分析，结果表明，OTPA能识别并分解出主要噪声源，并具有操作简便和省时的特点。

1 车内噪声的OTPA模型

利用传递路径分析方法对车内声压响应分析时，首先建立起系统的传递函数矩阵和车辆在行驶工况下的实际激励载荷。运行工况下传递路径分析方法利用参考激励替换原有激励载荷的概念：对于结构声激励源，一般选用第i个激励点一侧的加速度响应信号adi(t)代替激励力信号ei(t)；对于空气声激励源，一般选用第j个激励点附近的声压响应信号pdj(t)代替该点的空气体积速度Qj(t)。

根据传递路径分析方法的叠加原理建立车辆中多激励、多响应系统的传递函数方程组。假设系统存在多个（共计n个）激励参考点，其中结构声激励参考点为n1个；空气声激励参考点为n2个。同时考察多个（共计m个）响应点，建立系统在每一个频率点下的传递函数线性方程组，如公式（1）所示[7]。

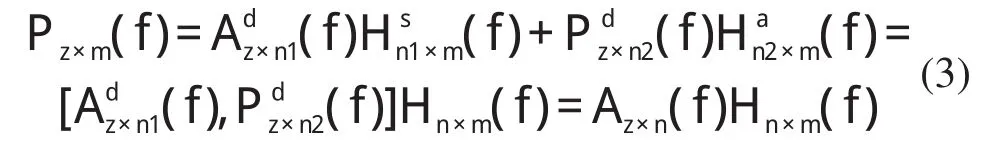
其中矩阵Az×n(f)为n个激励参考信号组成的矩阵，矩阵Hn×m(f)为n个激励参考点到m个声压响应点的传递函数矩阵。上述方程组中的各个量都是频率f的函数，也就是说对任一频率点就会产生一个新的方程组。此外，上述方程组中的各个量都是复数，它们同时包含着幅值和相位信息。

利用式（3），通过测量多组不同工况下激励参考点信号和声压响应信号就可以通过上述方程组求解出系统的传递函数矩阵Hn×m(f)。

在获取系统的传递函数矩阵后，利用测试得到的激励参考信号可以拟合车内响应点的声压响应。将拟合得到的声压响应与实际测量得到的声压响应分别在时域和频域进行比对，验证传递函数求解的有效性。以拟合车内第k个响应点的声压响应为例，给出运行工况下传递路径的计算分析流程，如图1所示。其中，FFT表示傅里叶变换。车内第k个响应点的声压响应可以描述为n1个结构声响应分量和n2个空气声响应分量的矢量叠加，从而可以识别出车内声压响应的主要声源及相应的传递路径。

明动信号进一步分析，可贡献要大于发动机舱和声音和舱的声压和哦古2 OTPA模型中传递函数的计算

将式（3）中的矩阵Az×n(f)进行奇异值分解

其中Uz×z和Vn×n称为矩阵Az×n(f)的奇异向量矩阵，均为酉矩阵，即满足：UTU=E1，VTV=E2，E1和E2分别为z×z、n×n的单位矩阵。Sz×n称为矩阵Az×n(f)的奇异值矩阵，为对角矩阵，对角线元素为σi(i≤n)，满足σ1≥σ2≥…≥σn≥0。奇异值数值的大小可以描述其包含矩阵Az×n(f)的信息量，定义奇异值σk的贡献率为

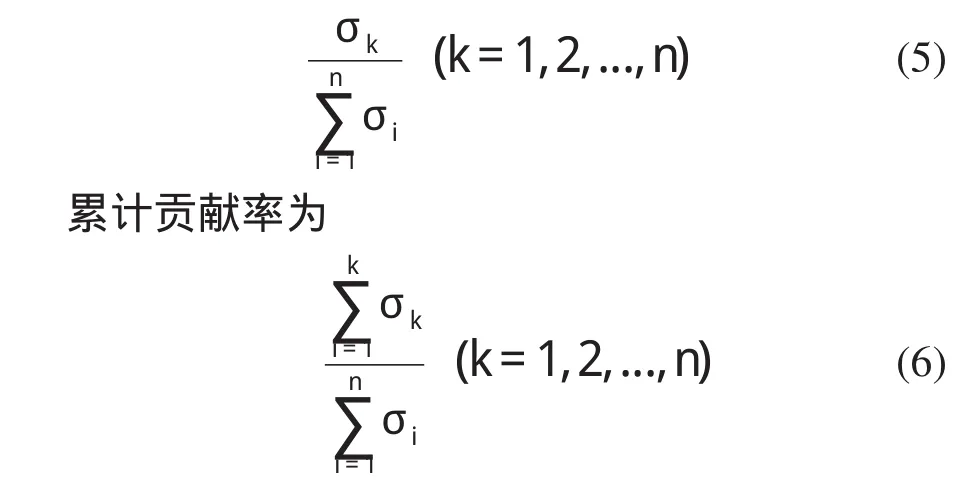
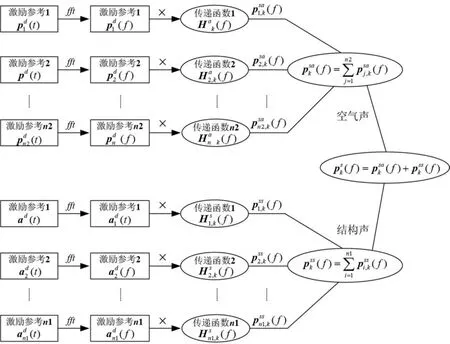
图1 传递路径分析方法拟合车内声压响应的计算流程Fig.1 Flow chart of OTPAapplied to vehicle interior noise

3 利用OTPA识别车内噪声的贡献

3.1 实验描述

研究对象为某乘用车。针对该车车内噪声声源和振源的情况及分析要求，实验中的传感器布置见表1。其中，编号1―7为结构声声源参考点，编号8―11为空气声声源参考点，编号12―14为响应点。

实验在转毂试验机上进行。实验工况包括不同档位下匀速（转速分别为1 600 r/min、2 000 r/min和2 400 r/min）、缓加速和急加速。

3.2 结果分析

以4档2 400 r/min匀速行驶的工况为例，以前排左侧座位右耳处实测的声压信号为响应信号，采用OTPA方法得到的车内噪声的拟合值和实测值在频域和时域的对比分别见图2、图3。

表1 OTPA实验的传感器布置Tab.1 Sensor placement of OTPAtests

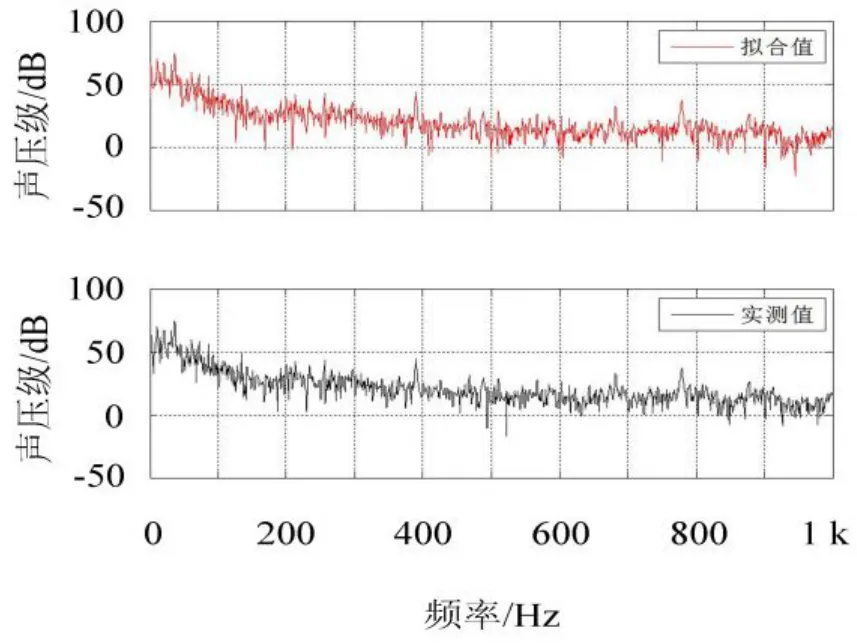
图2 OTPA拟合值和实测值在频域的对比Fig.2 Comparison between calculation data and test data in frequency domain

图3 OTPA拟合值和实测值在时域的对比Fig.3 Comparison between calculation data and test data in time domain

可见，计算结果和实测结果在频域和时域都能较好地吻合。进一步，应用OTPA对响应点的声压分解为空气声和结构声，结果如图4。

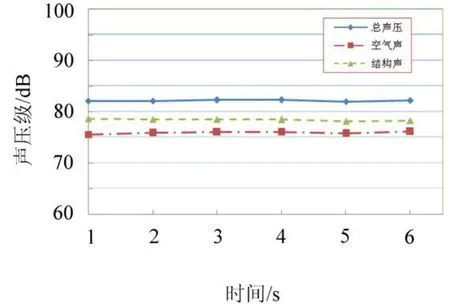
图4 总声压的进一步分解Fig.4 Further decomposition of the overall sound pressure

由图可知，结构声对总声压的贡献要稍大于空气声。对空气声进一步分解，结果如图5。

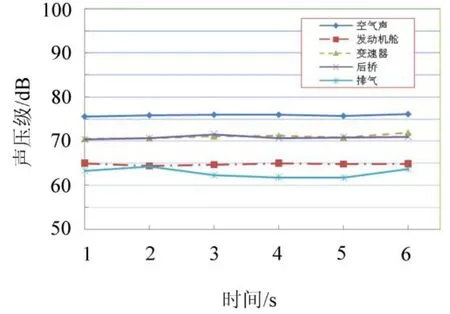
图5 空气声的进一步分解Fig.5 Further decomposition of airborne noise

可见，后桥和变速器处声音对空气声的贡献要大于发动机舱的声音和排气声。

对结构声进一步分解，结果如图6。表明座椅导轨的贡献度最大。

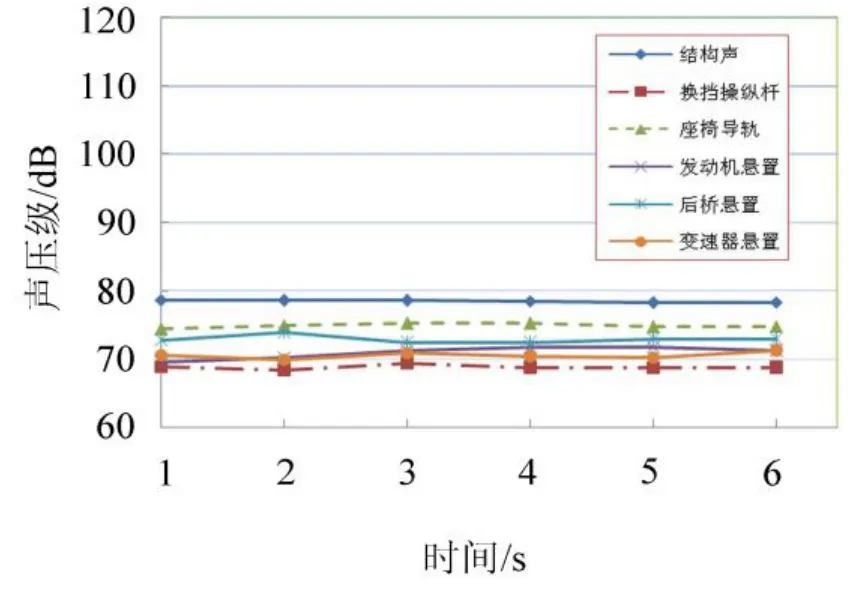
图6 结构声的进一步分解Fig.6 Further decomposition of structure-borne noise

对来自发动机左右悬置、后桥左右悬置、座椅和换挡操纵杆的振动信号进一步分析，表明：在座椅的三个方向振动中，X、Z方向振动的贡献比较大。在换挡操纵杆的三个方向振动中，Y方向振动的贡献比较大。在变速器悬置的三个方向振动中，Z方向振动的贡献比较大。发动机左右悬置的贡献度相当。后桥左右悬置的贡献度相当，右侧悬置的三个方向振动中，Y方向振动的贡献比较大，而左侧悬置的三个方向振动中，Z方向振动的贡献比较大。

4 结语

建立了车内噪声的运行工况传递路径分析模型，介绍了传递函数的求解算法。针对某乘用车，进行了运行工况下传递路径分析，获得了各个声源对车内噪声的贡献率。

分析结果表明，应用运行工况传递路径方法进行车内声源识别是可行的，该工作可为制定合理的车内降噪方案提供参考。

[1]H.Van der Auweraer,P.Mas,S.Dom,etc.Transfer path analysis in the critical path of vehicle refinement：the role of fast,hybrid and operational path analysis[J].SAE Technical Paper Series,2007-01-2352.

[2]Wyckaert,K.and Van der Auweraer,H.Operational analysis,transfer paths analysis,modal analysistools to understand road noise problems in cars[C].Proc.SAE Noise and Vibration Conference,1995,p 139-143.

[3]LMSInternational. Transfer Path Analysis: The qualification and quantification of vibro-acoustic transfer paths[M].LMS International Application Notes,1995:1-18.

[4]Juha Plunt.Strategy for transfer path analysis(TPA)applied to vibro-acoustic systems at medium and high frequencies[C].ISMA 23,16-18 September,Leuven,Belgium.

[5]Gert De Sitter,Christof Devriendt,Patrick Guillaume,etc.Operational transfer path analysis[J].Mechanical Systems and Signal Processing,2010,24:416-431）.

[6]Dmitri Tcherniak，yun S.Ryu. Developmentsin transmissibility matrix method in application for structure borne noise path analysis[C].2009 JSAEAnnual Congress.

[7]陆春.运行工况下车内噪声的声源识别及控制[D].北京：清华大学，2009.

[8]Jolliffe I T.Principal component analysis[M].New York:Springer-Verlag,1986.1-64.

[9]Partridge M and Calvo R A.Fast dimensionality reduction and simple PCA[J].Intelligent Data Analysis,1998,2(3).72-81.