基于卡尔曼滤波器的无传感器矢量控制
2013-02-23李壮,武欢
李 壮,武 欢
(辽宁铁道职业技术学院,辽宁 锦州 121000)
在生产和生活的许多方面,永磁同步电机由于具有效率系数高、抗干扰能力强以及稳定性好等优点被广泛应用。近年来高密度能量的磁性原料价格的下降,使得永磁同步电动机拖动相对地更具有竞争力,受到广泛关注。无速度和位置传感器矢量控制是近年来电动机控制的一个重要发展方向,也是衡量IPMSM高性能调速系统的重要指标。安装传感器存在很多问题:电机的尺寸过大会使电机成本提高;受到电磁噪声的影响,电机的运转性能和可靠性也会降低,导致电机的环境适应性下降;在石油挖掘机和压缩机驱动等特殊环境下不能装设传感器。高精度速度和位置估算能够克服无传感器控制带来的不足,对于IPMSM调速系统实现高精度控制具有很大意义[1]。
基于卡尔曼滤波器无传感器控制法(EKF)是通过对系统的模型误差和噪声的特性进行统计,利用最优化自回归对数据进行处理的方法,系统噪声被有效地抑制。卡尔曼滤波器充分利用了统计学规律,采用了递推算法,适应于变量多、耦合强的动态系统[2]。
1 基于卡尔曼滤波器的无传感器矢量控制
通过对定子电流矢量的幅值和相位的精确估计,达到控制定子交流量,最终改善电机转矩控制性能。电机交流量借助于坐标变换转化成两相同步旋转坐标系,使电机的各个空间矢量都变成了静止矢量。控制和被控矢量的各分量可以利用直接转矩控制等方法及时准确计算出来,转距控制所需矢量的各个分量值通过给定值来实现直流控制,等效成控制直流电动机。用变换坐标的逆过程,把这些直流给定量变换成原来坐标系,实现直流给定量到实际的交流给定量的转化,在三相静止坐标系上对矢量进行精确控制,达到实际值等于给定值[3]。
1.1 卡尔曼滤波器的线性与非线性问题
在已知系统噪声和测量噪声的数学模型里,卡尔曼滤波可以实现最小方差达到最优位置的估计。信号被卡尔曼滤波器处理后,原始信号就能准确快速分离出,滤波性能优良。在状态空间中,采用递推算法的卡尔曼滤波器可以适用于多维随机过程的位置估计。这种方法包含两种算法:离散型和连续型。随着微机技术的发展,很容易实现数字化,离散型的卡尔曼滤波算法逐渐得到了广泛应用。下面介绍一下离散型卡尔曼滤波器的原理[4]。
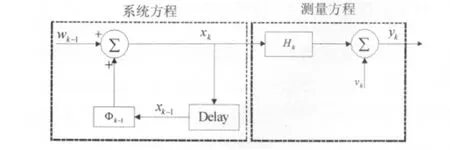
图1 离散、线性系统的方框图
系统的状态方程为:

其中,xk,xk-1分别是状态向量,wk和 vk分别是系统的过程噪声和测量噪声,Φk/k-1是转移矩阵。这里^xk为tk时刻的最优估计值,^xk/k-1为^xk的估计值,系统的状态估计误差 ~xk和先验估计误差~xk/k-1分别定义为:

在均方差极小的情况下,卡尔曼滤波实际上是状态的线性最小方差估计,进而得到状态变量的最优估计值。根据以上分析,可以给出卡尔曼滤波递推公式,包括预测和更新两个步骤。
第一步:预测。在已知先验估计的方差矩阵Pk/k-1的情况下,预测出先验估计值 ^xk/k-1以及 tk-1时刻状态变量的最优估计值^xk-1,求出卡尔曼增益Kk。

第二步:更新。利用最小方差原则,修正观测误差和先验估计值,求出最优估计矩阵Pk。
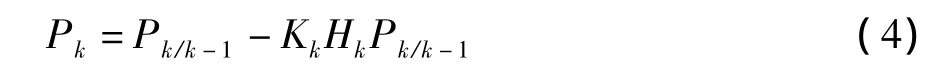
在初始值已知的情况下,可以看出离散型卡尔曼滤波器的公式是一个递推运算。通过不断“反馈校正”而形成的最小方差估计值,其最优线性滤波是无偏差估计。加权新的测量数据以及观测数据之间的偏差后,不断地修正先验估计值从而得到最优估计值[5]。
对于电动机控制系统,通过前面的研究,我们可以知道卡尔曼滤波公式是一个递推运算,这就需要一个给定初始值[6]。假如卡尔曼滤波器的系数矩阵是渐近稳定不变的,则随着滤波次数的增加,即使是不确定系统初始状态的特性和初始值,最优估计值最终将不受随意选取的初始值的影响,实现无偏差估计。收敛性也是影响卡尔曼滤波器滤波效果的关键。计算过程中的测量误差、模型误差以及可观测性误差都会影响卡尔曼滤波器的收敛性[7]。
1.2 IPMSM无位置传感器EKF控制模型
为了估计角速度ω的误差收敛为0,当id=0的时候,IPMSM无法实现高效率运转,所以需要假设ω=const和id=id=0的必要性。只有事先假定这两个条件,EMF模型的转子位置估计误差才会为零。如果第二个条件被满足,最优效率控制IPMSM的d轴电流id就不为负值[8]。
根据iαβ的状态方程得到:

在各种电机稳定运转条件下,为了使用卡尔曼滤波器,必须对目标参数进行设定。对于上式中的˙x(t)得到:
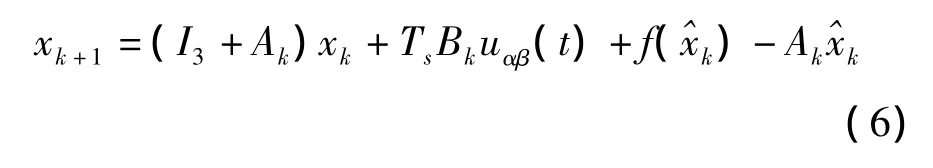
每隔采样周期Ts完成一次扩展卡尔曼滤波器预测和更新,在预测步骤中,进行下面的计算:

维持Pk|k对称性和正定性。因为电机的状态变量中包含角速度,所以状态变量为4,本方法中,通过调整模型参数,状态变量定义为3阶,所以减轻了EKF矩阵的计算量,同时使估计误差减小[9]。
2 仿真实验
根据无位置传感器系统结构图,速度调节的输出作为q轴电流给定i*q信号,这样就构成了内环为电流环,外环为速度环的电流速度双闭环调速系统[10]。

表1 IPMSM的参数设定

图2 起动特性
为了检测本方法的可用性,在无传感器驱动稳定运行时,使负载转矩在0.4s时刻以阶跃信号形式发生变化。
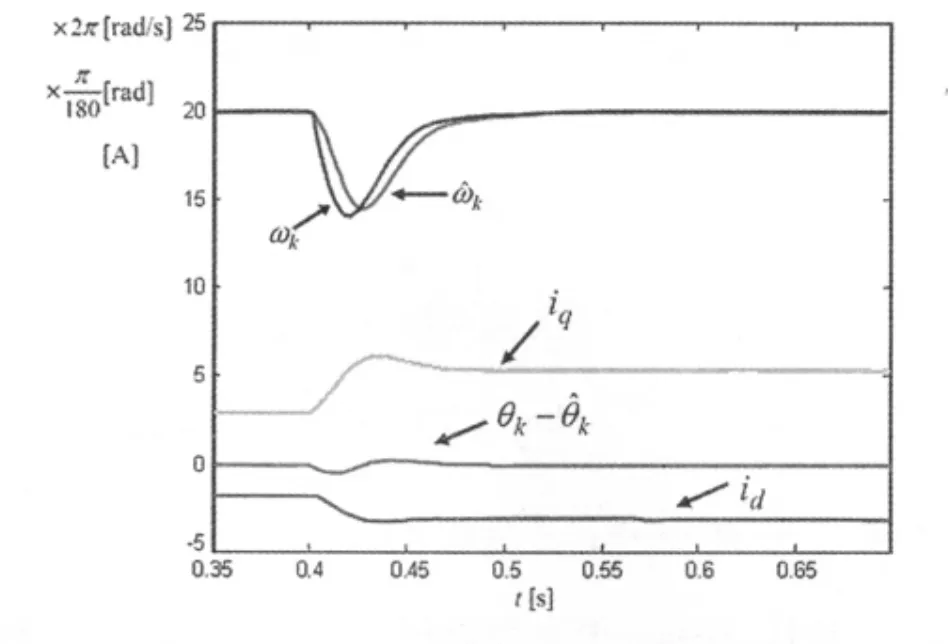
图3 负载转矩变化
由以上仿真曲线图可知,电动机参数改变对估计的结果影响不大,永磁同步电动机EKF控制调速系统的动态跟踪性也很好,卡尔曼滤波器控制调速系统也能获得较高的估计和控制性能。
3 结束语
永磁同步电动机在生产生活中大量使用,本文提出了基于卡尔曼滤波器无位置无速度传感器矢量控制,根据定子电流的幅值和相位的跟踪达到对转子位置的精确估计,从而实现无传感器的矢量控制,尤其在低速以及零速的情况下仍然能实现对转子的有效位置估计。
[1]胡崇岳.现代交流调速技术[M].北京:机械工业出版社,1998.
[2]许大中.交流电机调速理论[M].杭州:浙江大学出版社,1991.
[3]梁艳,李永东.无传感器永磁同步电机矢量控制中转子初始位置的估算方法[J].电工技术杂志,2003,22(2):10-13.
[4]谢宝昌.电机的DSP控制技术及应用[M].北京:北京航空航天大学出版社,2005.
[5]吴涛.基于TMS320F240的感应电动机矢量控制变频调速系统[J].机械,2007,34(6):39 -41.
[6]孙鹤旭,高晶,万文献,等.基于TMS320F2812的永磁同步电动机运动控制系统[J].电机与控制应用,2007,31(4):33-35.
[7]杨顺昌.电机的矩阵分析[M].重庆:重庆大学出版社,1988.
[8]杨贵杰.空间矢量脉宽调制方法的研究[J].中国电机工程学报,2001,21(5):79 -83.
[9]李峰,栋利,超英.基于DSP的SVPWM调制技术的研究[J].电气传动自动化,2005,27(4):1 -5.
[10]刘凤君.正弦波逆变器[M].北京:科学出版社,2002.
