STBC-OFDM 系统中有效降低计算量的盲接收机

贾兰芳

长治学院 电子信息与物理系，山西 长治046011

1 引言

正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）是多载波码分多址通信中的一种技术，由于数据在频率选择性衰落信道中传输时会引起码间干扰（Inter-Symbol Interference，ISI）[1]，从而导致性能严重下降，而OFDM 技术通过插入循环前缀和借助于傅里叶变换（IDFT/DFT）将频率选择性衰落信道变为窄带平坦衰落信道，可以有效避免ISI 和降低误码率，是下一代通信最具竞争力的方案之一[2-3]。空时分组编码（Space-Time Block Codes，STBC）是美国Cadence 公司的研究人员在Alamouti博士1998年提出的一种发射分集方案基础上提出的。STBC的最大特点是可以和多入多出（MIMO）技术有机结合，其缺点是STBC 的应用首先假设信道为平坦衰落，即信道参数为标量。而OFDM 技术正好可以弥补这一缺点，将二者结合构成的STBC-OFDM 系统，是提高无线频谱利用率的最有效的方法之一[4]。

盲多用户接收技术在DS-CDMA 系统中的应用已经有大量研究[5-7]，它在无需发送训练序列的情况下能有效消除多址干扰（Multi-Access Interference，MAI）。在各种盲多用户检测技术中，有基于最小输出能量的、有基于子空间的、有基于神经网络的，采用的递推算法有RLS（Recursive Least-Square）、LMS（Least-Mean-Squares）、Kalman算法等[8]，衡量多用户检测性能的好坏，主要是看其收敛速度的快慢以及计算复杂度的高低。尤其是计算复杂度成为盲多用户检测商用的一个瓶颈。而基于子空间的盲多用户接收机的解更接近MMSE 的解，且计算复杂度低[9]，所以被推广应用在STBC-OFDM 系统中。因为采用多天线发射，其计算量较DS-CDMA 系统的要大，阻碍了其应用[10]。本文从降低计算量的需求出发，提出了一种较低计算量的低复杂度的盲多用户接收机。

2 STBC-OFDM 系统模型

在MS 方采用两天线发射，在BS 方采用单天线接收（多天线接收可直接推广），小区中激活的用户共有K 个，用户k 的两组数据和在2i和2i+1 时刻，经过扩频调制、傅里叶逆变换（IDFT）再加上循环前缀（CP），再经过串/并转换后分别由天线1 和天线2 发射出去。两根天线上的扩频码分别为skp=[skp(0),skp(1),…,skp(N)]，p=1,2 代表发射天线1 和2。

在接收端，多个接收天线接收回来的信号经过串/并变换，移除CP 后，再进行FFT 变换，接收到的连续两个时刻的离散信号表示为：

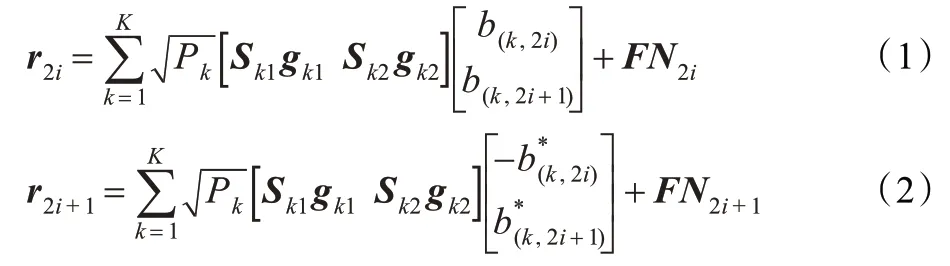
其中，Skp=diag(skp),F 表示N×N 的DFT 矩阵，其第(m,n)个元素为(1/)e-j2π(m-1)(n-1)/N,m,n=0,1,…,N-1,gkp=FLhkp,FL为F 矩阵的前L 列，hkp=[hkp(1),hkp(2),…,hkp(L)]T,L 为从发射天线p 到接收天线的信道的最大时延，hkp为与之对应的信道响应，N2i和N2i+1为加性高斯白噪声，是均值为0，方差为σ2的高斯过程。

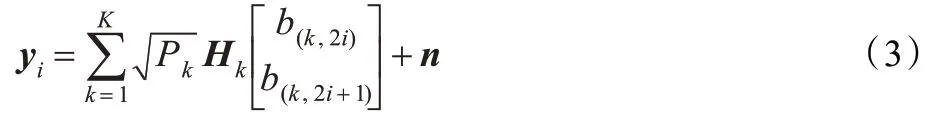
其中：

不失一般性，假设用户1 为期望用户，现在的问题是如何从y 中不失真恢复b。

3 STBC-OFDM 系统中的盲多用户接收机

3.1 基于子空间的盲多用户接收机

常规的盲多用户接收机在STBC-OFDM 系统中，首先表述为取代价函数：

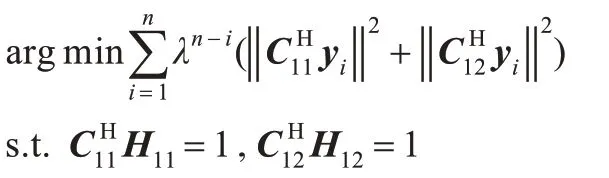
最优解很容易得到为：

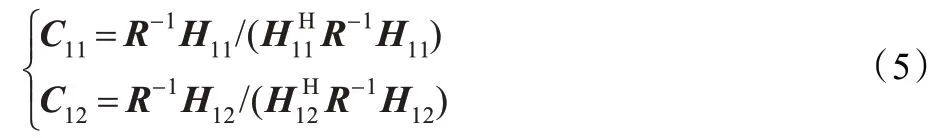
其中，含有矩阵的求逆计算量大，可采用递推算法求解，其计算复杂度为O(2×2N×2N)。

基于子空间的盲接收机是常规盲接收机的改进，首先对接收信号矢量求其自相关矩阵R 并进行奇异值分解，可表示为,其中Λs=diag(λ1,λ2,…,λ2k)包括2K 个最大的奇异值，Λn=σ2I2N-2K包括另外2N-2K个较小的奇异值，Us和Un分别称为信号子空间和噪声子空间，包括与Λs和Λn一一对应的互相正交、归一化的特征向量，且令C1i=UsC1si+UnC1ni，利用，取约束条件为(UsC1s1)HH11=1,(UsC1s2)HH12=1，由于C1ni没有出现在约束条件中，可得权值C1ni的最优解为0。由此得到一个基于子空间的代价函数：

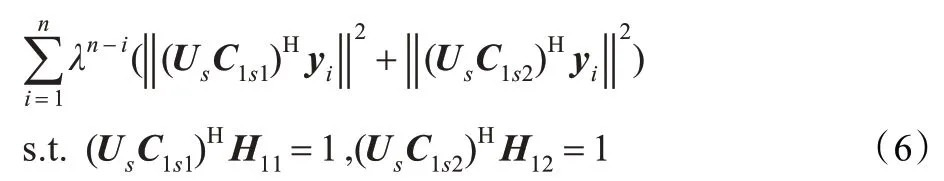
其最优解为[1]：

式中，含有矩阵求逆运算，计算复杂度高。可以采用递推算法求解，其计算复杂度为O(2×2N×2K)，一般N 远小于K ，基于子空间的计算复杂度要小于长规的盲多用户接收机。

3.2 信道估计

在式（5）和（7）中要求得最优权值，必须知道H11和H12的值，而H11和H12是未知的。因为信道h11和h12是未知的，下面来估计信道。

现有大量的基于子空间的盲信道估计方法[4]，可分别估计两传播路径的信道响应，但无法得到两条传播支路之间的相对幅相关系。而对STBC 解码而言，相对幅相关系非常重要。本节联合估计两支路的信道，从而确知两支路间的幅相关系。对期望用户而言，由于H11和H12位于信号子空间Us中，且Us和Un正交，可得：

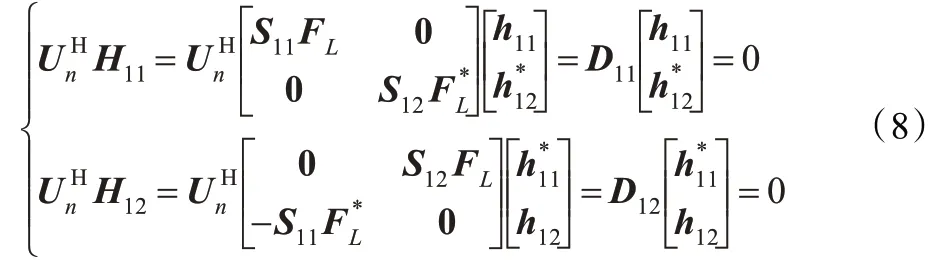
由式（8）得：

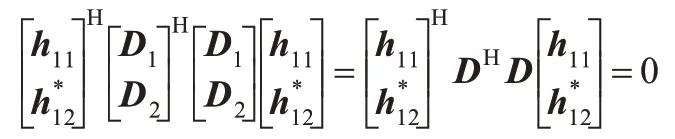
当S11≠S12时，矩阵DHD 存在唯一接近0 的最小特征值，与其对应的特征向量就是两信道h11和h12的估计结果，从而可得知H11和H12。其他用户的信道估计同H11和H12。

4 改进的子空间低复杂度的盲接收机

利用STBC 的特点，使得接收机的计算复杂度再次降低。接收信号的自相关矩阵是一典型的Hermitian 矩阵，可表示为，其中I2N表示2N×2N的单位阵，σ2为加性高斯白噪声的功率。Ω=diag(P1,…,PK,P1,…,PK)为实对角阵，Pk为用户k 的功率，B=[H11,…,HK1,H12,…,HK2]为2N×2K 矩阵。

现在来分析B 的特性，B 可表示为B=[H11,…,HK1,，那 么可得到：

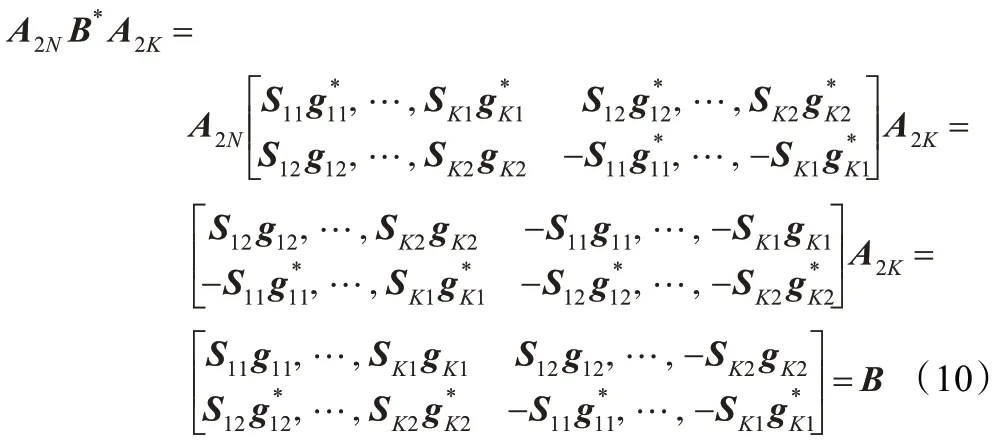
那么可得：

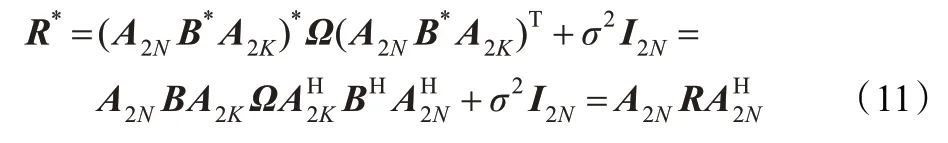
由于自相关矩阵为Hermitian 矩阵，同理可得到：

利用式（10）和（12），式（5）中的最优解C12可表示为C11和A2N的组合，即

也就说C12可通过C11直接求出，因而减少了一半的计算量。

由于Us和B 属于相同的信号子空间，且range(Us)=range(B)，因此Us能表示成B 的线性组合，可得到式（7）中的C1s2=A2NC*1s1。也就是说在对权值采用递推算法求解的时候仅需对权值C1s1求解。这样就相当于抽头个数减少了一半，使得计算复杂度降低。由以上推导，得到一个更为简化的代价函数：

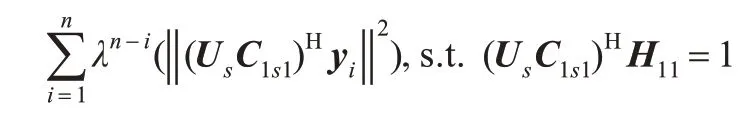
可得最优解为：

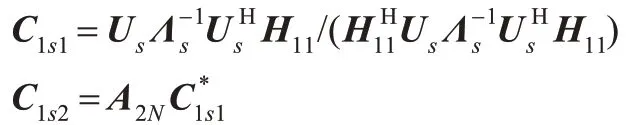
下面是提出的STBC-OFDM 系统中，基于子空间的盲接收机完整过程。因求逆运算量巨大，对其的求解采用RLS 递推形式来实现，令

递推算法如下：

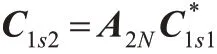
其中，H11的估计依赖于前面两信道h11和h12的估计结果。最后，发送的原始信息码就可通过抽样判决得到：。不难发现，由于将权值的求解放在了信号子空间，所以算法的收敛和跟踪能力会有很大提高。同时利用STBC 编码的正交特性，使得计算复杂度降低了一半，也即采用基于子空间的低复杂度接收机使计算复杂度由O(2×2N×2N)降为O(2N×2K)（N 远小于K）。仿真表明，在信道跟踪良好的情况下，在减小复杂度的前提下其误码率不会降低。

5 仿真结果

在频率选择性衰落信道下，对激活用户数为6的STBCOFDM系统采用Matlab进行仿真。采用BPSK调制，扩频码为31 位的GOLD 码，多径数为3，各用户的路径增益均采用相同随机数产生，噪声为均值为0，方差为0.1的加性高斯白噪声，遗忘因子λ=0.998。定义信噪比SNR=10 lg(P1/σ2)，信扰比为经过接收机后的期望用户能量和干扰能量（包括多址干扰和加性高斯白噪声干扰）之比，经整理为SIR=。在以下的仿真图中，将采用子空间且采用低复杂度解的接收机记为Sub-L，采用子空间但没有采用低复杂度解的接收机记为Sub-H，没有采用子空间但采用低复杂度解的接收机记为NSub-L。下面为仿真结果。

图1 比较了Sub-L 和NSub-L 的信扰比（单位为dB），SNR=20 dB，仿真对10 次取平均。图中横坐标n 为迭代次数，纵坐标为期望用户接收机的信扰比。系统中有6 个干扰用户，干扰强度相同为10 lg(Pk/P1)=18 dB。由图可看出基于子空间接收机的SIR 要比常规接收机的SIR 高，说明其抗远近效应的能力优，这是因为低复杂度解的基于子空间的接收机是在信号子空间求权值的。

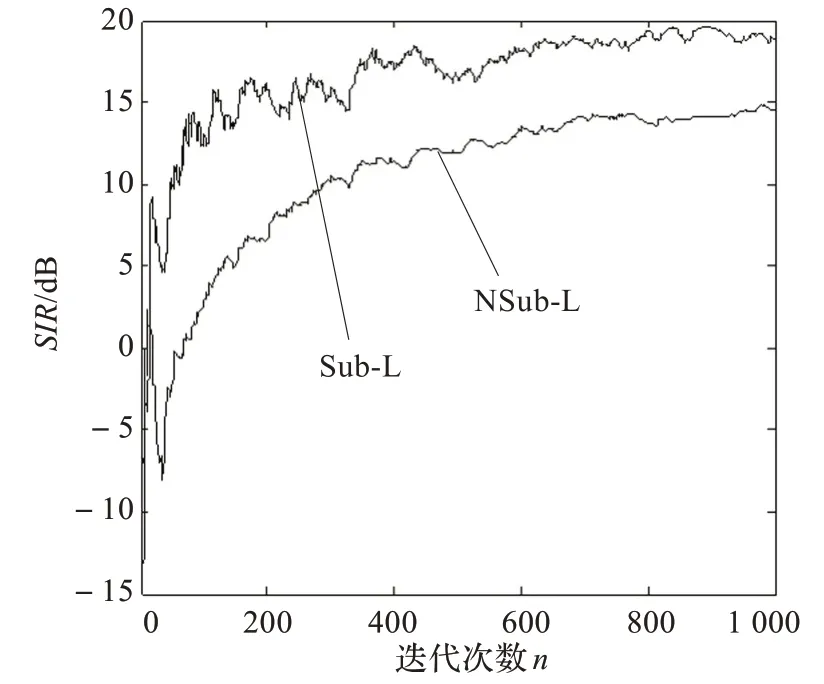
图1 Sub-L 和NSub-L 的SIR 比 较

图2比较了Sub-H、Sub-L 和NSub-L 接收机的BER，图中横坐标为输入的不同信噪比，纵坐标为用户1 的误码率。假设系统有6 个干扰用户，干扰强度为18 dB。由图可见，采用子空间技术的接收机无论高复杂度还是本文提出的低复杂度的接收机，两者误码率接近，从而证明了本文提出的接收机在有效降低一半计算量的同时其误码率不变，换言之，原来的常规高复杂度算法接收机存在冗余。本文利用STBC 码的特点，找到了权值之间的相关性，从而剔除了该冗余信息，在提高有效性的同时却不降低其可靠性。没有采用子空间技术的接收机其误码率相对较高，尤其在输入信噪比变大时，这是因为信噪比越大，信号子空间的能量就越大，从而使得基于子空间的检测优势更明显。

图2 不同接收机的BER 比较

图3比较了Sub-L 和NSub-L 在强干扰加入时的收敛速度。仿真环境同图1，开始干扰用户为6，干扰强度为18 dB，在迭代至1 500 次时加入28 dB 的强干扰。由图可见，两种接收机都能快速恢复到干扰加入前的状态，收敛速度较快。

图3 Sub-L 和NSub-L 收敛速度比较

6 结束语

本文讨论了STBC-OFDM 系统中的盲多用户接收技术。首先利用子空间分解的思想，将DS-CDMA 中的子空间技术应用到了STBC-OFDM 系统中，得到了在子空间内搜索的最优权值的解。通过分析发现该方法能有效地降低计算复杂度(由原来的O(2×2N×2N)降为O(2×2N×2K))同时加快了收敛速度。接着利用了STBC 编码的正交特性，推导出了STBC 中两个等效信道响应矩阵之间的关系，进而推导出了两个权值的计算关系式。在子空间的基础上又使得算法的复杂度降低了一半，为O(2N×2K)。最后仿真证明了所提出接收机能有效去除常规接收机本身的冗余度，使其在有效降低一半计算量的同时而其误码率不变，是一种简单可行的盲多用户接收机。本文的不足之处在于没有对信道估计展开进一步的研究，下一步将在STBC-OFDM 系统中对信道如何快速跟踪到信号子空间进行研究。

[1] Ali I，Doug N K，Jong S L.Blind adaptive multiuser detection for the MC-CDMA systems using orthogonalized subspace tracking[J].ETRI Journal，2009，31（2）：193-200.

[2] Wang R，Li H.A robust approach to channel estimation and detection for multi-carrier CDMA[J].IEEE Commum Lett，2006，10（2）：652-654.

[3] Wang X，Syrmos V L.Interacting multiple particle filters for fault diagnosis of non-linear stochastic systems[C]//Proceedings of Amer Contr Conf，2008：4274-4279.

[4] Yu J，Lee M，Chih C L.Multiuser receivers for MC-CDMA MIMO systems with space-time block codes[J].Signal Processing，2009，89（1）：99-110.

[5] 李立华，王勇，张平.移动通信中的先进信号处理技术[M].北京：北京邮电大学出版社，2005.

[6] 张贤达，保铮.通信信号处理[M].北京：国防工业出版社，2000.

[7] Daniele A，Ezio B，Marco L.Low-complexity receivers for multiuser detection with an unknown number of active users[J].Signal Processing，2010，90：1486-1495.

[8] Zhang X.Blind adaptive multi-user detection based on Kalman filtering[J].IEEE Trans on Signal Processing，2002（1）：87-94.

[9] De Lamare R C，Sampaio-Neto R.Blind adaptive MIMO receivers for space-time block-coded DS-CDMA systems in multipath channel using the constant modulus criterion[J].IEEE Transactions on Communications，2010，58（1）：21-27.

[10] Liu P，Xu Z.Blind MMSE-constrained multiuser detection[J].IEEE Transaction on Vehicular Technology，2008，57（1）：608-615.