甲型流感病毒HA蛋白质序列的预测

张 玲， 高 洁

（江南大学 理学院，江苏 无锡 214122）

流感是一种传染病，它具有一定的周期性和反复性，其在全球引起的发病率和死亡率非常高[1-2]。流感病毒基因组由8个独立的RNA片段组成，分别编码多个与病毒结构和病毒复制有关的蛋白质分子。其中，最受关注的蛋白分子是血凝素（hemagglutinin，HA）。血凝素蛋白与病毒易感的宿主范围和宿主对病毒感染产生的免疫反应有直接联系[3]。且蛋白质是生命的物质基础，没有蛋白质就没有生命[4]。因此，许多学者和专家研究甲型流感病毒并取得了一些成就。

他们从不同的角度研究流感病毒序列，且在寻找着最佳模型。李晓燕等对新型H1N1流感病毒HA基因特性分析[5]。基于聚类算法ModuleFind，梅娟等通过最大化蛋白质网络的模块性来寻找具有较强蛋白质结构的划分[6]。刘娟、任迪用时间序列的方法及整数阶差分和分数阶差分预测DNA序列[7-8]。基于CGR-游走模型，作者用分数阶差分的ARFIMA模型预测HA蛋白质序列。对所选取的1943～2013年同源性相对较高的71条蛋白质序列，我们用 ARFIMA（p，d，q）模型对前 20个位置去拟合并且预测除极个别外由预报区域图显示原始数据都在预报区域内，表明模型建立的比较合理，预报效果很好，这对流感病毒的研究和预测有着重要的意义。

1 方法

1.1 基于详细HP模型的蛋白质序列的CGR-游走模型

CGR是一种迭代映射技术[9]，2004年，喻祖国等人提出了基于详细HP模型的蛋白质序列的CGR方法[10]。在详细的HP模型中，将20种氨基酸分为四大类:非极性、负极性、无电荷极性和正极性，分别用 np、nep、up、pp 来表示，np={A，I，L，M，F，P，W，V}，nep={D，E}，up={N，C，Q，G，S，T，Y}，pp={R，H，K}。对于一个给定长为n的蛋白质序列S=s1s2Ksn，其中 si，i=1，2，…，n 是 20 种氨基酸中的一种，定义如下:

则得到一条序列 X（s）=c1c2…cn，其中 ci∈{A0，A1，A2,A3}。

再定义序列X（s）的CGR，类似于DNA序列的CGR定义，通过迭代过程得到该序列CGR CGRi=CGRi-1-0.5·（CGRi-1-ci），i=1，…，n，CGR0=（0.5，0.5）。

对于一个蛋白质序列，定义tk=yk/xk，其中yk是CGRk的y坐标值，xk是CGRk的x坐标值，则得到一个数据序列{tk:k=1，2，…，n}，把它作为一个时间序列，并称它为“CGR-游走序列”。

1.2 ARFIMA模型

定义 1 {εt}称为白噪声（white noise）序列[11]，简记为Xt～WN（μ，σ2）。 如果时间序列满足如下性质:

（1）任取 t∈T，有 EXt=u；

定义3 如果随机过程{Xt}是平稳的，且满足差分方程 Φ（B）▽dxt=Θ（B）εt，其中{εt}为白噪声序列，Eεt=0，Eεt2=σ2ε＜∞Θ（B）=1-φ1B-K-φpBp为 p 阶自回归系数多项式；Θ（B）=1-θ1B-K-θqBq，为 q 阶移动平均系数多项式，-0.5＜d＜0.5，则称{Xt}服从-0.5＜d＜0.5 的ARFIMA（p，d，q）模型[4]。

2 数据分析

选取同源性相对较高的71条流感病毒HA蛋白质序列（1943～2013年），数据来自 NCBI网站，其网址:http://www.ncbi.nlm.nih.gov/.

对于这71条蛋白质序列，选每一条序列的第三个位置为例来如下分析，首先把HA蛋白质序列转换成数值，定义:

得到相对应的HA蛋白质数值序列为:[0 0 0 1 0 0 3 0 0 0 3 0 2 2 0 3 2 0 3 0 0 0 2 3 3 0 0 2 2 2 0 3 3 0 0 0 0 0 3 2 2 2 0 3 0 0 0 0 3 0 0 2 0 0 0 0 0 3 0 0 3 2 0 2 0 3 0 3 3 3 2]，再 CGR 混沌游走，经过计算得到分数阶差分d=0.151，再取对数及0.151阶差分，可以得到一组新的数值序列:[0 0 0 0-2.833 -2.833 -2.833 2.026 6 2.026 6 2.026 6 2.026 6 4.852 5 4.852 5 0.233 6 0.084 16 0.084 16 1.322 5 0.361 1 0.361 1 1.569 1.569 1.569 1.569 2 0.067 0 1.109 5 1.940 23 1.940 23 1.940 23 0.168 8 0.060 7 0.026 64 0.026 64 1.194 6 2.060 9 2.060 9 2.060 9 2.060 9 2.060 9 2.060 9 5.700 8 0.412 71 0.157 0.070 55 0.070 55 1.211 4 1.211 4 1.211 4 1.211 4 1.211 4 4.337 4.337 4.337 0.121 16 0.121 16 0.121 16 0.121 16 0.121 16 0.121 16 4.174 7 4.174 7 4.174 7 6.356 4 0.446 03 0.446 03 0.106 61 0.106 61 1.461 4 1.461 4 2.839 6 3.754 3 4.542 2]，这 71 条序列的各个位置都要经过这样的预处理。

然后把这一组新的HA蛋白质序列转化成如图1所示的时序图 （CGR游走和取对数0.151阶差分），图中显示蛋白质序列在零上下波动，呈现出基本的平稳性。

图1 第三个位置对数差分后的时序图Fig.1 Time series figure of the third position sequence

图 2（ACF）和（PACF）为第三位置序列取对数再0.151阶差分后的自相关函数图和偏自相关函数图。序列的自相关图衰减迅速，而序列的偏自相关图衰减缓慢，这意味着原序列具有长记忆特征。

图2 对数0.151阶差分序列的自相关函数图和偏自相关函数图Fig.2 Sample ACF and PACF of the 0.151 order differenced log data of protein sequences

我们以纯粹的随机测试的分数差分序列，结果见表1。P＜0.000 1＜0.05，所以经取对数分数阶差分后此序列不是白噪声序列。因此，我们可以用ARFIMA（p，d，q）模型拟合该序列。

根据Akaike信息判别准则[12]，可选择ARFIMA（4，0.151，0）模型来拟合此每条序列的第三个位置序列。表2给出了模型的参数估计。

表1 白噪声检验Table 1 Autocorrelation check for white noise

表2 参数最小二乘估计Table 2 Conditional least squares estimation

从表中可以看出参数的P值都小于0.1，这表明 ARFIMA（4，0.151，0）模型能有效地拟合该序列。为检验该模型的合理性，选择了一个合适的检验统计量LB检验统计量[13]:

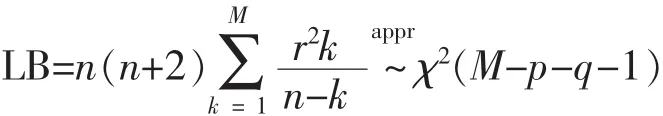
其中，rk是滞后的样本自相关函数，n是样本容量，M是一个取定的比n小的正整数。

表3显示了对于各滞后阶数，LB统计量的P值均显著大于0.1，意味着拟合模型的残差序列应为白噪声 （纯随机），因而可认为ARFIMA（4，0.151，0）模型能合理有效地拟合该序列。

表3 残差的自相关检验Table 3 Autocorrelation check of residuals

表 4则利用ARFIMA （4，0.151，0） 模型对 HA序列进行短期预测，即预测后十年2014～2023年第三个位置的预报值。（注:这些预报数据是混沌游走后取对数差分得到的，所以我们可以推出相应的数值。）

表4 2014-2023年的第三个位置的预报值Table 4 Forecast value of the third position for 2014-2023 year

从图3可以看出，除极个别外由预报区域图显示原始数据都在预报区域内，表明该模型建立的比较合理，预报效果很好。

根据上面对蛋白质序列的第三个位置的选择模型、参数估计、LB统计量检验，我们可以预测2014-2023年第三个位置的HA蛋白质序列的预报值为:3 2 1 0 1 1 1 1 2 2，进而可以预知2014-2023年第三个位置HA蛋白质是非极性、负极性、无电荷极性还是正极性。

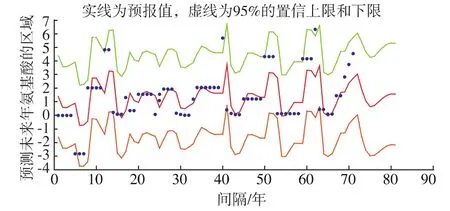
图3 预报区域图Fig.3 Forecast figure

3 结语

基于CGR混沌游走模型和分数阶差分模型，作者采取是一种纵向的预测方法，即用ARFIMA（p，d，q）模型预测未来年甲型流感病毒HA蛋白质序列。以1943～2013年这71条蛋白质序列的第三个位置为例，我们得到用 ARFIMA（p，d，q）模型对其前20个位置去拟合并且预测，发现除极个别外原始数据都在预报区域内除极个别外，表明模型建立的比较合理，预报效果很好。

我们可以用此方法分析和研究预测未来年的流感病毒蛋白质序列，这样节省大量的精力和财力。当然这种方法有一定的缺点，如选定的位置不足够多等，会影响预测值的精确性，还有待改进。

[1]Morens D，Folkers G，Fauci A.The challenge of emerging and re-emerging infectious diseases[J].Nature，2004，430:242-249.

[2]Muzaffar S B，Ydenberg R C，Jones I L.Avian influenza:an ecological and evolutionary perspective for waterbirdd scientists[J].Waterbirds，2006，29:243-257.

[3]Kobasa D，Takada A，Shinya K，et al.Enhanced virulence of influenza A viruses with the hae-magglutinin of the 1918 pandemic virus[J].Nature，2004，431（7017）:703-707.

[4]GAO Jie，XU Zhen-yuan.Chao game representation （CGR）-walk model for DNA sequences[J].Chinese Physics B，2009，18（11）:370-376.

[5]李晓燕，孔梅，陈锦英，等.新型H1N1流感病毒HA基因特性分析[J].中国卫生检验杂志，2010，20（12）:3121-3124.LI Xiao-yan，KONG Mei，CHEN Jin-ying.Analysis on the HA gene characteristics of novel influenza A （1H1N1） virus[J].Chinese Journal of Health Laboratory Technology，2010，20（12）:3121-3124.（in Chinese）

[6]梅娟，何正，王正祥，等.基于网络模块性的蛋白质序列聚类[J].食品与生物技术学报，2010，29（1）:123-127.MEI Juan，HE Zheng，WANG Zheng-xiang.Clustering protein sequences through modularity optimization[J].Journal of Food Science and Biotechnology，2010，29（1）:123-127.（in Chinese）

[7]刘娟，高洁.甲型H1N1流感病毒DNA序列碱基的预测[J].生物信息学，2011，9（3）:259-262.LIU Juan，GAO Jie.Forecasting bases for DNA sequences of influenza virus A/H1N1[J].China Journal of Bioinformatics，2011，9（3）:259-262.（in Chinese）

[8]REN Di，GAO jie.Early-warning signals for an outbreak of the influenza pandemic[J].Chin Phys B，2011，20（12）:128701-4.

[9]Jeffrey H J.Chaos game representation of gene structure[J].Nucleic Acid Res，1990，18:2163-2170.

[10]YU Zu-guo，Anh V V，Lau Ka-sing.Fractal analysis of measure representation of large proteins based on the detailed HP model[J].Physicas A，2004，337:171-184.

[11]王燕.应用时间序列分析[M].北京:中国人民大学出版社，2008.

[12]Akaike H.A new look at statistical model identification[J].IEEE transaction on Automatics Control，1974，19:9-14.

[13]Ljung G M，Box G E P.On a measure of lack of fit in time series models[J].Biomertrica，1978，30A:9-14.