数学美学观下的高职微积分课堂设计——以极限概念讲解为例

廖红文

（广东女子职业技术学院 广东 番禺511450）

高职数学课程的性质和任务一般强调数学是一门重要的专业基础课，为学生学好专业课打下必要的数学基础，提高学生的数学应用能力，培养学生运用数学分析问题、解决问题的能力。对于数学这样一门严肃、抽象、难懂的课程，大多数高职学生感到学得困难，缺乏兴趣，使得数学教育目标的实现大打折扣。古罗马诗人贺拉斯提出“寓教于乐”。有位学者曾说：“若要把感性的人变成理性的人，唯一的路径是使他成为审美的人。”基于这种背景和思想，我们提出从数学美学的角度出发设计微积分课堂，在教学中充分利用微积分美的内容、形式，运用审美的教学手段，培养学生的数学审美能力，真正发挥数学美的作用，激发学生学习微积分的兴趣。让学生从欣赏美的角度学习微积分，体会它的体系之美、简洁之美、符号之美、无限之美，在美的潜移默化中学习微积分的精髓。同时，培养学生运用数学的思想和方法思考问题、分析和解决问题的能力和学生理性思维习惯，培养学生追求真理、不畏艰辛、勇于自我批判的人文精神，提高学生的数学素养。

数学美的表现形式是多种多样的——从数学的外在形象上观赏，她有体系之美、概念之美、公式之美；从数学的思维方式上分析，她有简约之美、无限之美、抽象之美、类比之美；从美学原理上探讨，她有对称之美、和谐之美、奇异之美等。同时，数学还有着完美的符号语言、特有的抽象艺术、严密的逻辑体系、永恒的创新动力等特点。本文以极限的概念讲解为例，谈谈如何利用美学手段诱发学生的想象力学习数学，体验数学美。

创设课堂情景美

哈代说：“数学家跟画家或诗人一样，也是造型家，概念也像色彩或语言一样必须和谐一致。”在数学课堂上利用诗歌、绘画营造出优美和谐的环境，让诗歌和绘画诱发出学生的想象力，让学生在美的潜移默化中学习抽象的数学概念。实践证明，这是一种行之有效的教学模式。现代科学研究证明，接受信息者如果同时使用听觉和视觉，接受的效果更好，并且音像信号愈强，接受效果愈好。为此，在教学过程中，教师对学生就应努力强化这些信号。工整的板书、优美的图片、设计美观的多媒体都可以在课堂上创造令人赏心悦目的环境，不但可以提高学生的学习情趣，还可以大量减少语言的使用，使学生对数学有更直观的了解。

例如，“孤帆远影碧空尽，唯见长江天际流”——一句优美的诗配以滚滚长江的水墨画引入新一章的学习内容——极限。“孤帆远影碧空尽，唯见长江天际流”是李白在《送孟浩然之广陵》中的名句。学生齐颂李白《送孟浩然之广陵》拉开极限学习的序幕，而学生也在诗与画中沉浸在一种和谐的氛围里。这首诗让学生在脑海中勾勒出一幅“一叶孤舟随着江流远去，帆影在逐渐缩小，最终消失在水天一色之中”的图景，这时无穷小的数学概念也就融合在这美的诗意中去了。

再如，讲解无穷大的概念时，学生不能理解无穷大的那个预设的边界“M”时，我们引用“抽刀断水水更流”来解释“抽刀断水”与“M”的神似之处。讲解完无穷大，我们用陈子昂的《登高》配以一副意味浓浓的摄影作品对其作小结。“前不见古人，后不见来者，念天地之悠悠，独怆然而涕下”——从数学上看来，这是一首阐发时间和空间感知的佳句。前两句表示时间可以看成是一条直线（一维空间）。作者以自己为原点，“前不见古人”指时间可以延伸到负无穷大，“后不见来者”则意味着未来的时间是正无穷大。后两句则描写三维的现实空间：天是平面，地是平面，悠悠地张成三维的立体几何环境。全诗将时间和空间放在一起思考，感到自然之伟大，产生了敬畏之心，以至怆然涕下。这样的意境，让学生对无穷有了更深刻的理解。

课堂气氛和谐美

教师的教态和仪表向学生传递着课堂气氛的信息。亲切自然的教态、凝练朴素的语言、抑扬顿挫的语调，让学生感受到最直接的美学教育，让学生身心轻松地投入学习。风趣幽默的问题，在一问一答中建立起和谐的师生关系。数学课是思维的演练场，教师的任务之一就是要引导学生不断地思考，而提问是引导学生主动思维的有效手段。有人说，数学问题都是抽象和严肃的，怎么能让学生积极愉快地思考？这就关系到提问的技巧。首先，问题的表述要简单明了，语气要幽默，问题还要典型。例如，刚刚介绍完极限的概念后，提出一个问题：判断下列式子是否成立？

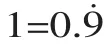
我们可以这样问：如果上式成立，1与0.9˙之间相差的那个数到哪里去了？由此引入极限史上的一个故事：“消逝的鬼魂”与无穷小量的产生。

故事的讲解不但让学生体会到极限是一个无穷变化的从量变到质变的过程，也体会到科学发展的曲折和艰辛，科学家永无止境的探索精神及对真理不懈追求的勇气。

数学思想深刻美

极限概念的引入是从单位圆面积的计算开始的。问题这样提出：让我们回到刘徽所处的魏晋时代，我们怎样计算单位圆的面积？学生在笑声中想象自己是刘徽，怎样来计算圆面积。

这个问题解决后，我们概括了三点内容。（1）逼近问题是一个与“变化”有关的问题。如果希望逼近一个不能直接计算的量，可以采用近似计算的技巧，而计算的精确度往往依赖于计算的次数。微积分（极限）可以解答精确度与计算次数之间的关系问题。如果增加计算次数，近似会无限接近某个数值，这正是逼近（或变化）的结果。（2）某些“量”的计算需要从变化的角度来处理，并通过“极限”过程来进行，这正是微积分的基本思想。（3）“以直代曲，逐步求精”的手段，是微积分中常用的方法。

随后，我们将这三点内容进行了拓展讲解，指出“化整为零，积零为整”就是在工作中拿到复杂的工作或任务时学会分解任务、分解难点、各个击破、再进行整合的方法。“以直代曲，逐步求精”就是在解决复杂问题时先用简单的模型代替实际问题，再逐步深入，逐步求精的方法。而这些方法可以用在我们工作的各个领域，是一种普适的解决问题的方法，从中也让学生体会到数学思想的深刻性和普适性。

数学思想是数学教学中的精华，是最能体现数学本质的东西。微积分中包含着丰富的数学思想。上面谈到的“极限思想”，“在微小局部‘以匀代非匀’，‘以直代曲’”的思想都是数学思想中的精髓。在讲授数学思想的课程中，笔者主要采用具体——抽象——具体的方法，通过典型实例引出问题，通过科学的抽象体现思想，再通过利用思想发现问题、解决问题的实例让学生领会思想。数学思想教育在培养学生创造力和独立思考问题的能力方面有着独到的价值。

数学哲学情操美

德育教育中有一种教育法叫无痕教育。无痕教育是指在教育过程中教育者通过创设有教育意义的情境和活动，既达到教育目的，又不留下让学生感到教育者在教育他们的一种方法。这种方法没有明显说理教育，而是把理寓于情境和活动之中，使学生在一种自然、轻松、愉快、美好的环境中心灵受到感化，自觉自愿地形成良好的思想品德。心理学研究表明：人们总有一种不太愿意整天被人教育的天性。前苏联著名教育家苏霍姆林斯基说过：“造成教育青少年困难的最重要的原因，在于教育目的在学生面前以赤裸裸的形式进行。”把教育目的隐藏起来，然后通过各种活动形式对学生进行“润物细无声”的无痕教育，会使学生在不知不觉中提高认识、净化心灵、规范行为。

微积分中饱含的深刻的人生哲学，对学生就是一种“润物细无声”的教育。例如，微积分讨论的连续函数绝大多数都是蜿蜒曲折的，有时上升有时下降，有极大值，有极小值。千姿百态的函数曲线像极了芸芸众生的命运，有时顺利有时曲折，有高峰时也有低谷时，这是人生的常态。所以，当我们处于人生佳境时不要骄傲，随时保持一颗谦恭之心；处于人生低谷时也不要气馁，只要我们继续努力，我们的人生曲线还能逐步上扬。

计算直线的长度比计算一条曲线的长度要容易得多。为了求得一条曲线的长度，把这条曲线无限细分，细分成若干条细小的直线，再把这些直线的长度加起来，就求得了曲线的长度。这就是学习极限时学过的“以直代曲”的思想，这也是微积分的基本思想。

我们可以将微积分的这种基本精神映射到人的一生。人的一生是在分分秒秒中度过，而这分分秒秒就是微分。人的一生不管有多长，都是这微小的分分秒秒的时间之和，这就是人生的积分。积分曲线的形态取决于微分函数。人生的积分曲线则取决于我们如何利用我们的分分秒秒——人生的微分函数。要想获得充实而有意义的人生，我们就必须抱有积极向上的人生态度，让我们在分分秒秒的努力中不断积累，收获我们丰盈的人生。

[1]张奠宙.微积分赏析漫谈[J].高等教育研究，2009（3）.

[2]杨忠泰.数学美学思想的历史演变[J].自然辩证法研究，2000（12）.

[3]周天良.无痕教育——有效的德育方法[J].素质教育大参考，2006（3）.