通用型无监督的无参考图像质量评价算法

任波波，杜海清，刘 勇

(北京邮电大学 网络体系构建与融合北京市重点实验室，北京100876)

责任编辑:时 雯

由于图像所承载的信息比文字、语音要丰富很多，越来越多的人们倾向于利用图像来传递信息或感知世界，而图像质量直接关系到感知客观世界以及认识事物的准确性，因此，对图像质量作出合理评价显得异常重要。

目前，图像质量评价算法主要分为两种，即主观评价和客观评价[1]。考虑到主观评价的不稳定性，易受人们情绪、周围环境影响等缺点，而且需要投入大量的人力、物力、财力，因此，主观评价算法的应用受到了一定的限制。根据其对原始图像的依赖程度，客观评价算法主要分为三种:全参考(Full-Reference，FR)、部分参考(Reduced-Reference，RR)以及无参考(No-Reference，NR)。全参考评价算法，往往会利用原始图片的全部信息，评价结果也比较符合人们的主观感知，典型代表有:结构相似度SSIM(Structural Similarity)[2]等。部分参考算法，顾名思义，需利用原始图像的部分特征信息，典型算法有:基于小波域自然图像统计模型的方法[3]等。然而，实际应用中，往往很难得到原始图像的参考信息，因而全参考以及部分参考算法的应用范围十分受限，而无参考算法的提出，打破了这一僵局。

无参考算法主要分为两种:针对特定失真类型的算法以及通用型算法。针对特定失真类型的算法，比较典型的是针对块效应的算法[4]以及针对模糊效应的算法[5]等。由于该类算法仅仅对特定的失真类型才奏效，因而其应用大大受限，而通用型算法能够适用于各种失真类型，是目前研究的热点。通用型算法又可分为两类。其一，不区分失真类型，该类算法不必对图像中的失真类型进行区分，通过提取有效特征，直接将特征向量映射至图像质量，关键是找到一种模型使得不同失真类型对该模型的响应不同，即模型需具备多分辨特性。典型算法有BLIINDS-I(BLind Image Integrity Notator Using DCT Statistics)[6]等。其二，“Two-Stage Framework”，即“两阶段架构”。该类算法分为两个阶段:第一阶段，对图像集进行训练来得到相应的失真分类器;第二阶段，针对不同失真来设计相应的评价算法，典型代表是BIQI(Blind Image Quality Index)[7]等。

此外，大部分通用型算法均是有监督的，需要主观分值的训练，比如CORNIA(Codebook Representation for No-Reference Image Assessment)[8]，BLIINDS-I和BIQI等算法。文献[9]于2012年提出了一种基于PLSA(Probabilistic Latent Semantic Analysis)[9]模型的图像质量评价算法，该算法克服了有监督的学习过程，是一种真正无监督的评价算法。鉴于上述针对特定失真类型以及有监督学习的局限性，本文提出了一种无监督的通用型无参考质量评价算法，最后，在LIVE图像库上进行测试，验证了算法的有效性。值得注意的是，该算法基于自然图像，对于人工图像没有进行相应的测试。

1 算法描述

考虑到感兴趣区域更能吸引眼球以及自然场景图像的边缘主导特性，提取特征分为两个部分:显著块和边缘块的提取。由于变换域提取特征过于复杂，本文直接提取空域特征，算法结构框图如图1所示。首先，通过视觉注意模型取得训练图像集的显著块以及利用Canny算子提取其边缘块，该训练图像集是无失真图像和失真图像的混合体，将提取到的显著块和边缘块构成一簇特征向量，然后对特征向量进行归一化及ZCA(Zero Components Analysis)处理[8]，最后进行K-MEANS聚类而得到特征池，考虑到计算机内存问题，采用分层聚类，即先在每幅图像内部进行聚，类然后在图像间进行聚类，至此，特征池的构造完成了。其次，对无失真图像和测试图像也进行相同的处理，只是不进行聚类，实验过程保证了训练集与测试集互不相交。最后，通过ANN(Appropximately Nearest Neighbour)得到无失真图像和测试图像关于特征池的分布，进行相似性度量以及最小合并，从而得出分值。

图1 基于特征池的通用型无监督的无参考图像质量评价算法结构框图

1.1 特征池的构造

所谓特征池，就是包含多种特征的“池”，池中的特征通过一定的比例聚集成一幅幅图像，即一幅幅图像是由特征池中的特征向量构成的，或者说，图像是这些特征向量的抽象表示。因而，给定一幅图像，即可利用这些特征向量来表征它。特征池的构建非常关键，由一组无失真图像和失真图像经过特征提取、聚类等步骤提炼而成。

本文直接从空域提取特征，考虑到人类的视觉感知特性，从感兴趣区域中提取显著块以及利用Canny算子提取边缘块。取块过程中，块的大小固定为7×7，得到的特征向量维数为49。文中采用文献[10]的视觉注意模型，如图2所示。为了尽可能多地提取感兴趣区域特征，还需进行一些后续的处理。由于显著区域往往都是不规则的，本文利用一个矩形框来无限地逼近这个显著区域，通过选取一个阈值，将显著性MAP中所有小于该阈值的像素点置为0，反之，则置为1，这样就得到了矩形框，然后将矩形框与原始图像对应像素点相乘，最后将全0行或全0列剔除掉就近似得到了感兴趣区域。为了避免损坏原图像的结构信息，并不是将所有的全0行或列剔除，这里以行为例来解释其中原理，列与行的处理完全相同。从第一行开始，将所有全0行剔除直至遇到第一个非全0行，然后再从最后一行开始，剔除所有全0行直至遇到第一个非全0行，阈值为原显著性MAP的均值，如图2c、图2d所示。最后，在感兴趣区域中随机取块即可得到显著块。

图2 感兴趣区域的提取

本算法基于灰度图像进行处理，并没有考虑颜色信息，图2b、图2d中亮的部分即标识了显著区域，而且图2c、图2d要比图2a、图2b的尺寸小，这是经矩形框逼近删除掉一些无用信息后的缘故。图2c、图2d分别是图2a、图2b的浓缩版本，这样从图2c中随机取块时，就可以尽可能多地提取到感兴趣区域特征。

图3为提取显著块的结构框图，实验过程中，将每幅图像提取的显著块数量固定为4 000，这就意味着，对于一幅给定的图像，能够得到一个49×4 000的显著块特征矩阵，其中49表示的是特征向量的维数，而4 000表示的是显著块的个数。

图3 显著块生成框图

算法通过Canny算子提取边缘像素，然后通过计算边缘像素在图像块中的比例是否超过某一阈值来提取边缘块，该阈值的选取与文献[11]一致，即取为0.002。考虑到图像边缘保留了原始图像中相当重要的信息，所以，本文将提取给定图像的所有边缘块。当然，边缘块的块大小与显著块是一致的，图4为一幅图像提取到的部分边缘块。边缘块的提取框图如图5所示。

图4 原始图像及其部分边缘块

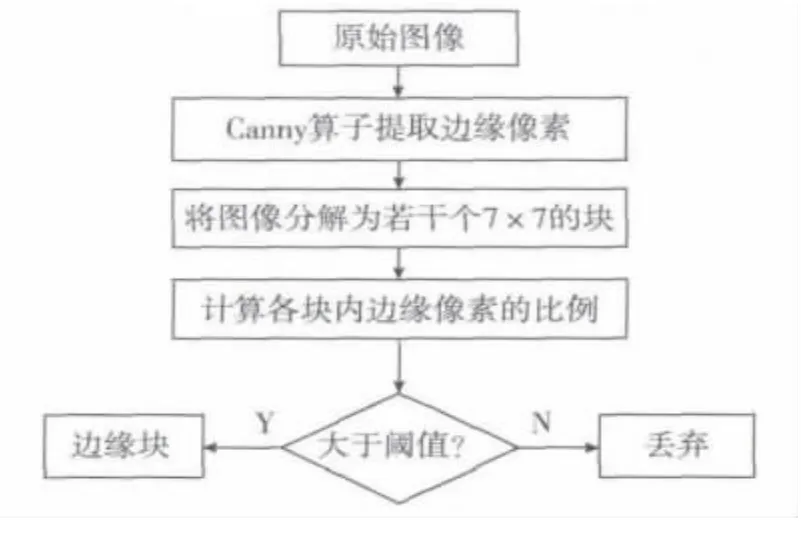
图5 边缘块提取框图

接下来是预处理过程，先进行归一化，然后再进行ZCA白化处理。归一化过程如下

式中:Ⅰ是由显著块和边缘块组成的特征矩阵，其每一列为1个49维的向量，列数代表了从原图像中提取到的块数，即显著块和边缘块的总数目;μ为Ⅰ的均值向量，而σ为其标准差向量，两者维数均为提取到的总块数;C为常数，为了防止分母为0的情况。

ZCA白化处理的目的是去相关，图像中相邻像素间是高度相关的，经过ZCA白化处理后能够降低原始数据的冗余度。其实，这是人眼特性的一个近似模型，人眼感知图像时，不会将所有像素点传至大脑，这样冗余度很大，视网膜就起了一个解相关的作用，来降低像素间的相关性，这与白化处理是一致的。

预处理完成后，通过K-MEANS对白化后的数据进行聚类，选取的聚类中心为10 000个，即特征池的大小设置为10 000，之所以选取10 000，至此，特征池构造完成。

1.2 无失真图像与测试图像的处理

所谓无失真图像，就是没有失真的图像，理论上认为无失真图像是完美的。本节引入无失真图像的目的是为了将测试图像与无失真图像关于特征池的分布进行相似性度量，继而得到测试图像的客观分值，需要注意的是无失真图像并不包含测试图像集的原始图像。

对于无失真图像，先提取空域特征，即提取其显著块和边缘块，特征提取完毕后，先归一化特征矩阵，然后ZCA白化处理，此过程与构造特征池中提取空域特征无异。测试图像与无失真图像的处理类似，唯一不同的是，特征矩阵经白化处理后分为两部分:一部分为边缘块特征，另一部分为显著块特征。显然，经过上述一系列操作，无失真图像得到一个特征矩阵，而测试图像得到两个，一个为显著块特征矩阵，另一个为边缘块特征矩阵。

1.3 质量分值的计算

在此之前，先对一些符号及术语作简要的描述，以便于后文的理解。

首先，特征池中包含有若干个特征向量，每一列即代表一组特征向量，总共有10 000组特征向量。在此，将每一组特征向量称为word，特征池就是由许多个word构成的“池”。

其次，图像关于特征池的分布，记为p(z|Ⅰ)，其中Ⅰ表示给定图像集，Z表示特征池，其每一列即为一个word，该表达式的含义是，特征池中各个word在一幅图像中发生的概率。

通过1.2节可以得到无失真图像以及测试图像的特征矩阵，由1.1节又能得到特征池的各个word，本节通过ANN(Appropximately Nearest Neighbour)来得到给定图像的特征分布。ANN是由David M.Mount和Sunil Arya用C++开发，它可以在数据集中查找到与给定数据最为相近或相似的一组数据。本算法中，它被用来在特征池中查找与给定特征矩阵最为相似的一组word，进而得到给定图像集中各个word发生的概率，即p(z|Ⅰ)的值。

由上文可以得到无失真图像的特征分布，记为p(z|Iref)。注意，算法中选取的无失真图像不止1幅，而是23幅，所以通过ANN能够得到23幅图像关于10 000个word的分布，简单来说，就是得到一个23×10 000的矩阵，每一行对应一幅图像，10 000列分别对应的是该图像中10 000个word发生的概率。

对于测试图像来说，由于特征矩阵分裂为边缘块的特征矩阵和显著块的特征矩阵，所以，应该得到两种分布，记为p(z|Iedge)和p(z|Iinterest)，分别对应测试图像的边缘分布以及显著分布，两者均为m×10 000的矩阵，其中m表示的是测试图像的数量。

接下来就是测试图像与无失真图像的相似性度量，这里有多种距离度量方法，比如欧氏距离、卡方距离、街区距离等等。本算法采用卡方距离，卡方距离的计算公式为

由此可以得到p(z|Iref)与p(z|Iedge)以及p(z|Iref)与p(z|Iinterest)的卡方距离，分别记为和两者皆为23×m的矩阵，m仍表示测试图像的数目。

最后，客观质量得分为

其中，α+β=1。由于采用与无失真图像分布的距离来度量图像质量，所以PSCORE值越小，表示差距越小，越接近无失真图像的质量，图像的质量也就越好。实验过程中发现当α=0.9，β=0.1时，算法性能相对较好，由此可见边缘块对图像质量的重要性。图6为α和β取不同值时的算法性能比较。

图6算法性能随的变化曲线

图6 中的PLCC和SROCC是评价算法性能的两个指标，两者的值越大，说明算法性能越好。图6是在固定特征池大小为10 000的情况下，通过实验1 000次，然后取PLCC和SROCC的中位值得到的。

2 性能评估及分析

本文算法利用LIVE图像库进行测试，该图像库有29幅无失真的原始图像以及经过5种失真处理后的图像，5种失真类型分别为JPEG2K，JPEG，WHITENOISE，GBLUR和FASTFADING。为了验证算法与人们主观分值的一致性，采用如下拟合函数形式[11]

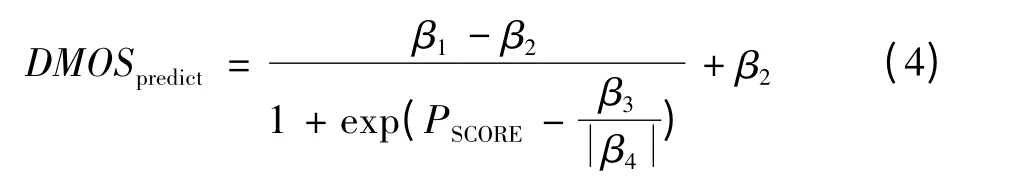
式中:β1，β2，β3，β4是拟合参数，通过对主观DMOS的最佳拟合得到，再利用上式得到DMOSpredict，DMOSpredict是预测的DMOS，DMOS越大，表示与原始图像的差距越大，其质量也就越差;PSCORE是本文所提算法得出的客观分值。选用以下两个参数来评价算法性能:1)PLCC(Pearson Linear Correlation Coefficient)，Pearson线性相关系数，该参数主要用来评价模型的预测精确性;2)SROCC(Spearman Rank Order Correlation Coefficient)，Spearman等级次序相关系数，该参数主要用来评价模型的单调性。两者的值越大，表示算法性能越好。

实验过程中，选取LIVE图像库[12]中80%的原始图像及其所有失真图像用于构造特征池，20%的原始图像及其所有失真图像用于测试算法性能，这样可以保证训练图像集与测试图像集互不相交。为了与文献[9]保持一致，算法同样实验1 000次，每次随机选择23幅原始图像及其所有失真图像来构造特征池，剩余的6幅原始图像及其所有失真图像用于评价性能的好坏，最后取1 000次迭代实验后PLCC和SROCC的中位值作为评价指标。本文算法模型的预测值与主观DMOS的拟合曲线如图7所示。其中，图7是在PLCC取中位值的情况下得到的，ALL表示测试图像中包含各种失真类型。

2.1 图像质量评价算法性能比较

本文选用一个全参考的质量评价算法PSNR[1]和两个无参考的质量评价算法CORNIA[8]、文献[9]的算法来进行比较。性能参数如表1所示，表中的ALL表示测试图像包含各种失真类型。

图7 模型的预测值与主观DMOS值的拟合曲线

表1 迭代实验1 000次PLCC和SROCC的中位值

总体来说，CORNIA性能最好，本文算法与全参算法PSNR可比拟，PSNR在WN失真上性能要好于本算法，但本算法在GBLUR及FF失真上好于PSNR。此外，文献[9]也是一种无监督的通用型无参考评价算法，而本文算法的总体性能相比文献[9]有所提高，尤其在WN，GBLUR和FF失真上性能均要远优于文献[9]。对于CORNIA算法，它是一种通用型无参考算法，但是该算法最后计算分值时需借助SVR(Support Vector Regression)以及DMOS值来训练模型，因而它并不是无监督的，而本算法无需主观分值的训练，是真正无监督的。

2.2 特征池的大小对算法性能的影响

本节通过改变特征池的大小，分别将其大小设置为200，400，800，1 000，2 000，5 000，10 000，15 000，图8给出了算法性能随特征池大小的变化曲线，可以看到，随着特征池大小的增加，性能有所提高，当超过10 000时，性能又会下降，所以本算法中将特征池大小设置为10 000。本图是通过实验1 000次，然后取PLCC和SROCC的中位值而得到的。

3 结论

图8 性能随特征池大小的变化曲线

本文通过构造特征池来对多种失真类型进行评价，特征池如同一本字典，可以简单地认为图像就是由特征池中的一个个word构成，本算法基于这样的假设，认为不同类型的失真会导致失真图像关于word的分布不同，因而通过与无失真图像的word分布进行比较，就可以得到客观分值，该值是一个与无失真图像差距的度量，其值越小，表示与无失真图像越相似，质量越好。实验结果证明了本算法的有效性，正是基于这样的假设，避开了有监督的学习过程，从而实现了一种无监督的图像质量评价算法。当然，本算法也有一定的局限性，前期需要通过训练来构造特征池，并不是一种“盲”的通用型算法，然而提出一种盲的通用型图像质量评价算法是很有意义的，也是十分困难的，这是下一步的研究方向。

[1]袁飞，黄联芬，姚彦.视频质量客观评价技术研究[J].电视技术，2007，31(3):91-94.

[2]WANG Z，BOVIK A，SHEIKH H，et al.Image quality assessment:from error visibility to structural similarity[J].IEEE Trans.Image Processing，2004，13(4):600-612.

[3]WANG Z，SIMOCELLI E.Reduced-reference image quality assessment using a wavelet-domain natural image statistic model[C]//Proc.SPIE Human Vision and Electronic Imaging.[S.l.]:SPIE Press，2005:149-159.

[4]WANG Z，SHEIKH H，BOVIK A.No-reference perceptual quality assessment of JPEG compressed images[C]//Proc.2002 International Conference on Image Processing.[S.l.]:IEEE Press，2002:477-480.

[5]FERZLI R，KARAM L.A no-reference objective image sharpness metric based on just-noticeable blur and probability summation[C]//Proc.2007 International Conference on Image Processing.[S.l.]:IEEE Press，2007:445-448.

[6]SAAD M，BOVIK A，CHARRIER C.A DCT statistics-based blind image quality index[J].IEEE Signal Processing Letters，2010，17(6):583-586.

[7]MOORTHY A，BOVIK A.A two-step framework for constructing blind image quality indices[J].IEEE Signal Processing Letters，2010，17(2):587-599.

[8]YE P，KUMAR J，KANG L，et al.Unsupervised feature learning framework for no-reference image quality assessment[C]//Proc.IEEE Conference on Computer Vision and Pattern Recognition(CVPR).[S.l.]:IEEE Press，2012:1098-1105.

[9]MITTAL A，MURALIDHAR G，GHOSH J，et al.Blind image quality assessment without human training using latent quality factors[J].IEEE Signal Processing Letters，2012，19(2):75-78.

[10]HOU X，HAREL J，KOCH C.Image signature:highlighting sparse salient regions[J].IEEE Trans.Pattern Analysis and Machine Intelligence，2012，34(1):194-201.

[11]NARVEKAR N，KARAM L.A no-reference image blur metric based on the cumulative probability of blur detection[J].IEEE Trans.Image Processing，2011，20(9):2678-2683.

[12]SHEIKH H，WANG Z，CORMACK L，et al.LIVE image quality assessment database release2(realigned subjective quality data)2006[EB/OL].[2013-02-05].http://live.ece.utexas.edu/research/quality/.