压缩感知图像重建算法的研究现状及其展望

李 然，干宗良，崔子冠，朱秀昌

(南京邮电大学 江苏省图像处理与图像通信重点实验室，江苏南京210003)

责任编辑:时 雯

1 压缩感知简述

近年来，压缩感知(Compressive Sensing，CS)成为一个快速发展的研究领域，受到了广泛关注。CS的基本思路是:假设长度为N的离散时间或空间信号在某变换域的系数是稀疏的或可压缩的，随机生成M个与信号长度相同的测量向量，与信号作内积运算得到相应的M个观测值，其中M远远小于信号长度N，若将这M个观测值看作是变换系数，测量过程显然违反离散信号的频域采样定理，导致无法从这些观测值中无失真复原信号，但CS理论表明，通过利用信号本身的稀疏或可压缩的性质，在测量向量满足一定条件时，仍可以欠奈奎斯特速率无失真复原信号[1]。随着CS理论的不断发展，该理论已经成功地应用在了压缩成像、无线传感网络、医疗成像、雷达、通信、遥测、天文学等许多领域[2]。

与传统的图像压缩技术相比，图像压缩感知并不是对显著变换系数进行编码压缩，而是构造随机测量向量直接下采样图像信号，以降低图像维数的方式来达到压缩效果。由于在压缩过程中，不必对图像进行全变换以及复杂的显著系数编码，从而大大降低了编码复杂度。另外，压缩感知的随机下采样操作甚至可在光域内直接进行(例如，单像素相机[3])，因此可降低图像采集设备的分辨率，节省资源消耗。然而，图像压缩感知也面临着若干难题，其中最主要的包括:随机测量矩阵的存储量较大和图像重建算法的性能问题。通过分块测量[4]和结构化测量方式[5]，可有效地减少测量矩阵的存储量。对于图像重建算法，由于图像的维数较高(可达百万像素)，所以计算复杂度是亟待解决的问题。另外，各种重建算法的不同机制也会对图像的重建质量造成影响，这也是目前该领域关注的热点之一。

本文在对目前压缩感知重建算法的文献进行分析和综合的基础上，首先阐述了压缩感知的基本原理及其各项关键技术，然后简要总结了目前流行的压缩感知图像重建算法，接着给出各种图像重建算法的仿真结果及分析，最后总结了目前压缩感知图像重建算法存在的问题及研究展望。

2 压缩感知模型及图像稀疏性

2.1 压缩感知的数学模型

CS理论是建立在Candes等人[6-7]和Donoho[8]具有突破性的工作之上，表明了在某变换域具有稀疏或可压缩性的信号可由少量随机线性测量值(远低于奈奎斯特采样频率)无失真地复原。CS理论的实现包含3个要素:稀疏性或可压缩性、非相关测量以及最优化重建，其中稀疏性或可压缩性是CS的必备条件，最优化重建是CS复原信号的手段，非相关测量是CS重建算法的收敛保证[9]。CS的数学描述如下:

假设长度为N的一维离散信号x(若该信号为二维图像，则按光栅扫描的方式拉成一维)，考虑到由M个长度为N的列向量φi按行组成的矩阵，作矩阵运算得到相应的长度为M的列向量y

式中:一般称φi为测量向量;Φ为测量矩阵;y为观测向量。假设测量矩阵Φ行满秩，则当M远小于N时，仅已知观测向量y，由线性代数知识可知，该线性方程的解有无穷多个，且原始信号x必是其中之一。如何从无穷多个解中成功地找出原始信号，就是CS所提出的数学问题。为了解决该问题，需要获取一些关于原始信号x的先验知识，稀疏性或可压缩性就是最常运用到的先验知识。

2.2 图像的稀疏性或可压缩性

假设存在L个长度为N的列向量ψi按列组成的矩阵Ψ=[ψ1，ψ2，…，ψL]，且其可线性表示离散信号x，即

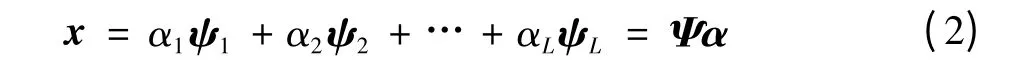
式中:一般称ψi为稀疏基底;Ψ为稀疏矩阵;α为表示向量。若α仅有K个分量不为0，其余均为0，即可称信号x在Ψ域中具有稀疏性，K为信号的稀疏度。然而，自然界中的信号如语音、图像信号，一般在Ψ域中并不具有严格稀疏性，而是K个分量具有较大幅值，其余分量的幅值与之相比微乎其微，这种情况一般称信号x在Ψ域中具有可压缩性[10]。

对于图像信号来说，常用的稀疏基底是DCT基和小波基。除了图像信号在这两种基底下具有较好的可压缩性外，它们存在快速变换法也是其流行的重要因素。对于图像这种大规模信号，稀疏变换是否存在快速变换法往往会成为其是否可应用于实践的关键。根据快速变换法可构造出相应的稀疏算子Ψ(·)，作与式(2)相同的稀疏表示

信号本身具有的稀疏性或者可压缩性可当作先验知识，用于求解CS重建问题，以下将简要介绍各种CS重建算法。

3 压缩感知图像重建算法

3.1 图像重建算法

利用信号的稀疏性或可压缩性，最直接的方法是采用最小L0范数模型求解CS问题

考虑到作CS测量时，可能混入一定噪声，所以采用不等式约束，ε为较小的常数，用于度量噪声水平。由于L0范数的非凸性，使得直接求解式(4)在多项式时间内无法完成[11]。为了使CS问题得以求解，各种替代模型及其相对应的CS重建算法被提出，有如下4类:

1)凸松弛(最小L1范数)算法

此类方法采用L1范数替代L0范数去度量表示向量α的稀疏度，变非凸问题为凸问题，使CS问题得到求解。所使用的最小L1范数模型为

式(6)也就是著名的基追踪去噪(Basis Pursuit Denoising，BPDN)模型[12]，可化为二阶核规划(Second-order cone program，SOCP)问题，采用l1-magic工具箱[13]求解。

除此之外，式(6)还可化为无约束的凸优化问题，即

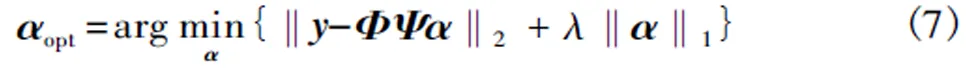
式中:λ为正则化因子，用于平衡目标函数加号前后两项对全局的影响。该式在统计机器学习研究领域也被称为LASSO(Least Absolute Shrinkage and Selection Operator)模型[14]，用于解决回归问题，求解该式目前流行的算法是GPSR(Gradient Projection for Sparse Reconstruction)算法[15]。

2)贪婪算法

此类方法仍是使用式(4)作为模型求解，或者假设α的稀疏度为K，采用式(8)求解

式(8)采用的策略是尽最大可能以最少的表示系数去减少y与ΦΨα之间的残差能量。目前流行的贪婪算法为:OMP(Orthogonal Matching Pursuit)算法[16]、CoSAMP(Compressive Sensing Matching Pursuit)算 法[17]、StOMP(Stagewise OMP)算法[18]以及SAMP(Sparsity Adaptive Matching Pursuit)算法[19]，其中前两者使用式(8)求解，后两者使用式(4)求解。

3)迭代硬阈值算法

迭代硬阈值(Iterative Hard Thresholding，IHT)算法[20-21]采用式(8)作为求解模型，其基本思路是:从凸集Ω={α:y=ΦΨα}上某初始点开始，采用硬阈值方法缩减α到K稀疏，再利用凸集投影法(Project onto Convex Set，POCS)将估计解重新投影回凸集Ω，如此反复迭代，直至满足收敛条件。IHT法的计算复杂度很低，十分适合于图像这种大规模信号的CS重建，但其对初始点的要求很高，使得它很难应用于实际。然而，对于分块压缩感知(Block Compressed Sensing，Block CS)的图像重建[4]，它的一种变体——平滑投影Landweber算法(Smoothed Projected Landwebe，SPL)[4，22-23]在很短的时间内获得了较好的图像重建效果，受到了广泛关注，这主要得益于Block CS可提供较好的初始解——图像的线性最小均方误差(Minimum Mean Square Error，MMSE)估计。

4)贝叶斯学习算法

文献[24-26]提出的贝叶斯压缩感知(Bayesian Compressive Sensing，BCS)将机器学习领域的稀疏贝叶斯学习(Sparse Bayesian Learning)与CS相结合，利用相关向量机(Relevance Vector Machine，RVM)学习算法[27-28]进行CS重建信号。通过构造出一种高斯概率密度模型来解释表示向量α的稀疏性，将观测向量y的各分量看作是学习样本，通过RVM训练出概率模型的相关参数，从而确定出α的概率分布，取其期望值作为最优解αopt。

5)最小全变差算法

除了上述利用信号的稀疏性或者可压缩性作为先验知识外，对于CS图像重建而言，仍可利用其他的先验知识，其中以像素域的平滑性或者说梯度域稀疏性最为常见，其原因是大多数有意义的图像均是分段平滑信号。梯度域稀疏性的数学度量通常使用全变差(Total Variation，TV)范数[6]

式中:(t1，t2)是图像g的像素坐标;D1为垂直方向上的差分D1=g(t1，t2)-g(t1-1，t2);D2为水平方向上的差分D2=g(t1，t2)-g(t1，t2-1)。因此，利用图像梯度域稀疏性的先验知识，图像CS重建问题可采用最小TV模型求解

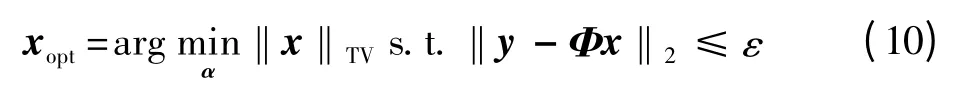
若要使上述所有CS重建算法可收敛到原始信号或者接近于原始信号，仍需要使测量矩阵Φ与稀疏矩阵Ψ满足一定条件，这就是CS重建信号得以成功的关键因素——非相关测量。

3.2 图像的非相关测量矩阵

只有当测量矩阵Φ与稀疏矩阵Ψ不相关程度较大时，才有可能使上述CS重建算法在测量次数M远小于信号长度N的情况下收敛到原始信号或者原始信号附近。度量这种不相关程度的方法主要有3种:Φ与Ψ混合相关度[29]、A(=ΦΨ)的受限等距性(Restricted Isometry Property，RIP)[30]以及A的Spark值[31](即A的最小线性相关组的列向量个数)。目前，重建算法的收敛分析更多地采用A的RIP性质来度量Φ与Ψ之间的不相关度。那么，满足RIP的Φ与Ψ的组合有哪些呢?文献[32-33]证明了以下3种随机矩阵Φ与任意的固定矩阵Ψ在满足式(11)的条件时，即

式中，C为常数。

组成的A以压倒性概率遵从RIP性质:

1)高斯随机矩阵:M×N的随机矩阵，任意元素φij均相互独立，服从均值为0、方差为1/M的高斯分布。

2)正交高斯随机矩阵:首先产生N×N高斯随机矩阵，再利用施密特正交化法使矩阵各列向量相互正交，最后随机选取M个行向量生成M×N矩阵。

3)二值贝努利随机矩阵:M×N的随机矩阵，任意元素φij均相互独立，各以1/2概率取

那么，采用以上3种随机测量矩阵和任意固定的稀疏矩阵，在满足式(11)的前提下，上述所有CS重建算法都能够在可容许的误差范围之内重建信号，只是对于不同算法，常数C的取值或大或小。可通过定义过测量因子d[34]简化式(11)为

式中:d=C·ln(N/K)，可知过测量因子d是由所选的重建算法、信号长度N和信号稀疏度K共同决定的。通过大量的实验显示，过测量因子d取4时即可使CS重建算法有效收敛[2]。

采用随机测量矩阵的一大优势是可使CS测量具有通用性[35]，即在设计测量系统时，不需要确定稀疏矩阵，仅在重建信号时，再考虑稀疏矩阵的选择。然而，对于大规模信号，例如图像信号，其相应的随机测量矩阵所需的存储空间巨大(可达吉字节以上)，同时测量过程的计算复杂度较高，因此，使测量系统难以在实际场合实现[29]。目前解决这一问题的方案有两种，第一种是受JPEG的分块DCT变换启发，提出的Block CS，即将图像分成大小相同互不叠盖的宏块，产生相应的随机测量矩阵进行测量[4]。由于分块尺寸较小，存储测量矩阵所需空间和计算复杂度均会大大较低;另一种方案就是采用具有快速测量法的测量矩阵构建测量系统，例如随机扰乱实傅里叶矩阵(Scrambled Real Fourier Ensemble，SFE)[7，36]和结构化随机矩阵(Structurally Random Matrices，SRMs)[5，37]，这些矩阵的快速测量方法使用了流行的快速傅里叶变换(Fast Fourier Transform，FFT)、离散余弦变换(Discrete Cosine Transform，DCT)或沃尔什—哈达玛变换(Walsh-Hadamard Transform，WHT)，在测量信号时不必构造测量矩阵，而只进行等价的变换，即

式中:Φ(·)代表测量函数或算子。为了使测量系统不失去通用性，该算子在进行上述快速变换之前，先将原始信号进行有规则的扰乱，变换后再随机下采样为M个观测值。快速测量法的应用虽然解决了存储量和计算复杂度的问题，但在重建信号时引入了一定局限性，使得必须选择具有快速变换法的稀疏矩阵和支持快速测量法的重建算法，这些均加大了重建信号系统实现的复杂度。

4 仿真结果及分析

为了测试本文所提到的所有CS图像重建算法(如表1所示)的性能，采用SRMs中的随机扰乱块哈达玛变换(Scrambled Block Hadamard Ensemble，SBHE)构造测量算子，对整幅图像进行非相关CS测量。由于贝叶斯学习算法(命名为Bayesian_RVM)和SPL算法仅支持分块测量矩阵，所以采用高斯随机矩阵对每个图像块进行测量，分块尺寸为32×32。产生随机测量算子和矩阵的伪随机序列的生成方法采用Marsaglia的极坐标算法(Polar Algorithm)[38]，种子取为0。对于稀疏矩阵Ψ的选择，除SPL算法外，均采用存在有快速变换法的Daubechies-4正交小波基，SPL算法的稀疏矩阵采用复值双树小波(Complex-valued Dual-tree Discrete Wavelet，DDWT)。测试图像为5幅不同类型的512×512灰度图像Lena，Barbara，Peppers，Mandrill和Goldhill，如图1所示。运行算法的硬件平台为主频为2.80 GHz的双核CPU计算机，软件平台为32位的Windows7操作系统和MATLAB 7.6仿真实验软件。

图1 本文所使用的5幅测试图像

表2～表6列出了不同测量率下各种图像重建算法的性能指标，采用PSNR值对重建图像质量进行客观评价;为了能够反应重建图像的主观视觉质量，采用了结构相似性指标SSIM(Structural Similarity Index)值进行评价;对于算法的计算复杂度，采用重建时间进行度量。首先，比较各种算法的PSNR值，可看到利用图像梯度稀疏先验的min-TV算法在各种测量率下均获得最高值，所以min-TV算法十分适合用于CS图像重建。仅次于min-TV算法，利用图像平滑和稀疏先验的SPL算法也获得了较高的PSNR值，基本与min-TV算法相差1 dB左右。其他仅利用图像稀疏先验的算法中，基于梯度投影的GPSR算法和自适应判断稀疏度的贪婪算法SAMP算法重建图像的PSNR值较高，但远低于min-TV算法(相差4 dB左右)。同样，可看到在贪婪算法中StOMP算法的性能极不稳定，在测量率为0.1时，恢复Lena和Mandrill图时未能保证算法收敛，产生了很大的误差，所以这种带有阈值收缩的StOMP算法在应用图像重建时，鲁棒性不强。对于IHT算法和基于RVM的贝叶斯算法获得PSNR值也不高，所以此两类算法用于图像重建时，也不能有效提升图像质量。接着，通过SSIM值来反应图像的主观质量，可看到与PSNR值的情况相似，仅有min-TV算法和SPL算法获得了高SSIM值，其余算法远低于这两种算法。在测量率为0.1～0.3时，SPL算法的平均SSIM值均超过min-TV算法，那么可知SPL算法在低测量率下的主观视觉质量与min-TV算法相近。图2也展示了在测量率为0.2时，SPL算法和min-TV算法重建Barbara图的主观视觉比较，可看出min-TV算法重建出的图像并不光滑，存在有大量的噪声，而SPL算法重建出的图像较光滑，主观视觉质量良好。最后，比较各种算法的计算复杂度，可看到计算复杂度最高的算法是min-TV算法，所以min-TV算法复原图像的高质量是以计算复杂度为代价。同时可看到，计算负担较轻的算法是贪婪类算法，例如，StOMP算法和SAMP算法，这两种算法重建时间相似，但SAMP算法的稳定性更强，所以在贪婪类算法中最适合图像重建任务的算法是SAMP算法，该算法复原图像质量于GPSR算法相近，在测量率为0.2～0.5时，重建时间仅需2～4 s，远低于GPSR算法(需30 s左右)。对于SPL算法，该算法的复杂度不高，平均重建时间仅在30 s左右，计算量仅是min-TV算法的十分之一，然而，复原图像质量与min-TV算法相差不大，所以，可综合评判出SPL算法是性价比最高的图像重建算法。

表2 测量率(M/N)=0.1时各种图像重建算法的性能比较

表3 测量率(M/N)=0.2时各种图像重建算法的性能比较

表4 测量率(M/N)=0.3时各种图像重建算法的性能比较

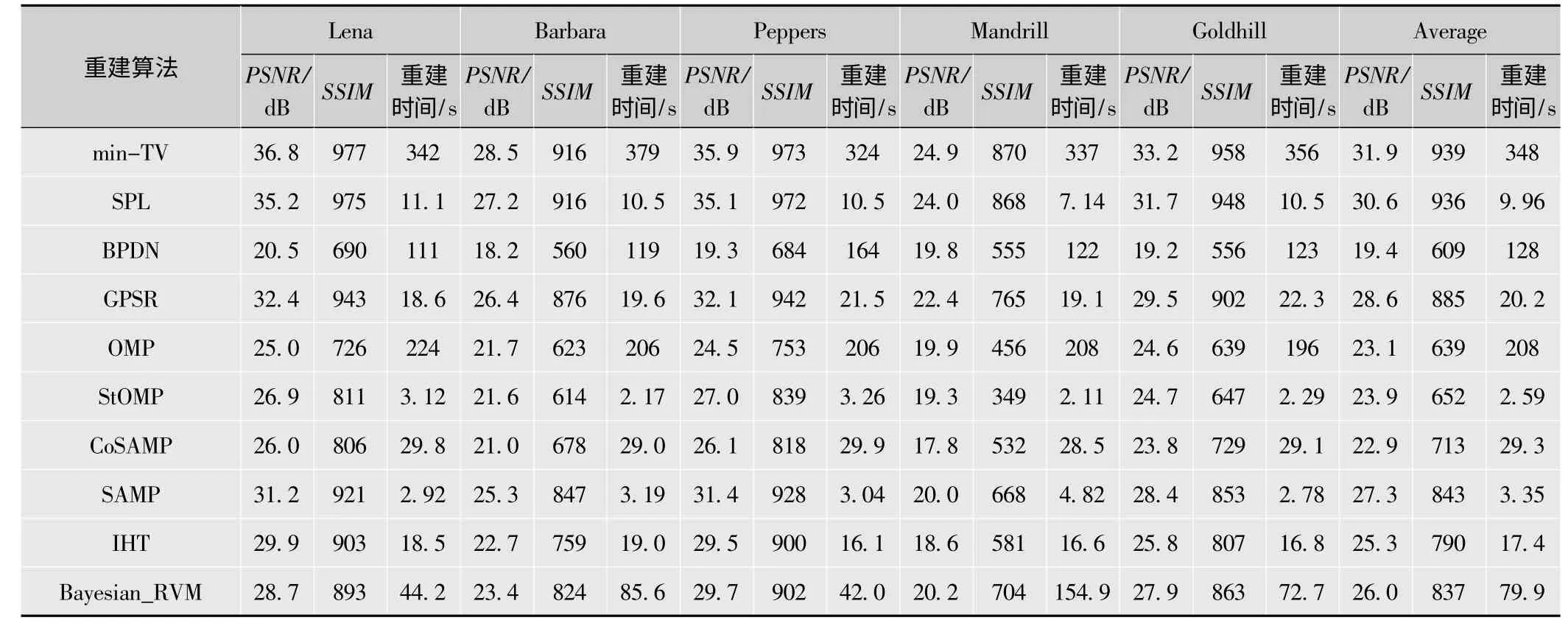
表5 测量率(M/N)=0.4时各种图像重建算法的性能比较

表6 测量率(M/N)=0.5时各种图像重建算法的性能比较

图2 测量率为0.2时，采用min-TV算法和SPL算法重建Barbara图像对比

5 结论和研究展望

压缩感知是当前信号处理尤其是针对图像视频信号处理研究的一个热点，课题研究具有重要的理论意义和应用价值。图像压缩感知的基本思想与传统图像压缩有着明显的区别，它是一种新的图像编码框架，其主要特点是编码简单，解码复杂;拥有与传统的图像编码器相媲美的压缩效率[39];随机测量方式使得其抗误码性能较好，非常适合于便携式、耗电低、运算能力受限的无线图像采集节点。所以图像压缩感知作为未来无线传感器网络中静止图像压缩的可选方案具有较大竞争力[40]。压缩感知图像重建算法作为图像压缩感知在工程应用中的关键，具有很大的研究价值。

目前压缩感知图像重建算法的研究已经获得了很多较有意义的成果，然而距离实用还有不少的差距，仍存在尚需进一步研究的问题，主要有以下几个方面:

1)图像先验知识的使用

目前在重建图像信号时，一般使用的先验知识是图像变换域和梯度域的稀疏性。文献[41-42]提出使用其他的图像先验知识(例如，块稀疏、小波分解系数之间的相关性)进行CS重建，获得了良好效果。所以在未来压缩感知图像重建领域，如何更好地使用图像其他的先验知识(例如，非局部相似性)，将会受到更多的关注。文献[23]借助视频中多假设概念，充分利用了图像空间相关性作为先验知识，就是该方面应用的实例。

2)图像去噪算法与CS重建法的融合

文献[43]提出的基于图像去噪BM3D算法的CS重建法，提供了设计重建算法的新思路。其他的图像去噪算法，例如，K-SVD去噪、PCA去噪等，是否也能融合到CS重建算法呢?文献[22]巧妙地将小波去噪算法融入SPL算法，获得了很好的效果。这也指明未来CS图像重建算法的新方向。

3)CS图像重建法的鲁棒性

由于CS测量过程总是会引入噪声，所以CS重建算法的鲁棒性是十分值得关注的问题。在实际工程应用中，为了传输信号，往往会先对信号进行量化处理，由此引入的量化噪声，如何在CS重建过程中消除，也是研究的热点。对于大规模的图像信号，这两种噪声更是很大程度地影响CS重建图像的质量，在重建过程中对图像去噪，也是在工程实践中亟待解决的问题之一。

4)CS重建算法计算复杂度与图像重建质量的权衡

计算复杂度过大是CS重建算法实际应用的一个障碍，单一地降低复杂度，又会对图像的重建质量造成影响。二者之间的权衡也是CS图像重建算法中需要考虑的问题。

[1]RICHARD G.Compressive sensing[J].IEEE Signal Processing Magazine，2007，24(4):118-121.

[2]CANDES E，WAKIN M.An introduction to compressive sampling[J].IEEE Signal Processing Magazine，2008，25(2):21-30.

[3]DUARTE M，DAVENPORT M，TAKHAR D，et al.Single-pixel imaging via compressive sampling[J].IEEE Signal Processing Magazine，2008，25(2):83-92.

[4]GAN L.Block compressed sensing of natural images[C]//Proc.International Conference on Digital Siagnal Processing.Cardiff，UK:IEEE Press，2007:403-406.

[5]DO T，GAN L，NGUYEN N，et al.Fast and efficient compressive sensing using structurally random matrices[J].IEEE Trans.Signal Processing，2012，60(1):139-154.

[6]CANDES E，ROMBERG T，TAO T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J].IEEE Trans.Information Theory，2006，52(2):489-509.

[7]CANDES E，ROMBERG J，TAO T.Stable signal recovery from incomplete and inaccurate measurements[J].Communications on Pure and Applied Mathematics，2006，59(8):1207-1223.

[8]DONOHO D.Compressed sensing[J].IEEE Trans.Information Theory，2006，52(4):1289-1306.

[9]焦李陈，杨淑媛，刘芳，等.压缩感知回顾与展望[J].电子学报，2011，39(7):1651-1662.

[10]CANDES E，ROMBERG J.Practical signal recovery from random projection[C]//Proc.SPIE Computational Imaging.[S.l.]:IEEE Press，2005:76-86.

[11]ELAD M.Sparse and redundant representations[M].New York:Springer Science+Business Media，LLC，2010.

[12]CHEN S，DONOHO D，SAUNDERS M.Atomic decomposition by basis pursuit[J].SIAM Journal on Scientific Computing，1998(20):33-61.

[13]CANDES E，ROMBERG J.L1-magic:Recovery of sparse signals via convex programming[EB/OL].[2012-09-22].http://users.ece.gatech.edu/justin/l1magic/downloads/l1magic.pdf.

[14]TIBSHIRANI R.Regression shrinkage and selection via the lasso[J].Journal of the Royal Statistical Society Series B，1996(58):267-288.

[15]FIGUEIREDO M，NOWAK R，WRIGHT S.Gradient projection for sparse reconstruction:application to compressed sensing and other inverse problems[J].IEEE Journal Selected Topics in Signal Processing，2007，1(4):586-597.

[16]TROPP J，GILBERT C.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Trans.Information Theory，2007，53(12):4655-4666.

[17]NEEDELL D，TROPP A.CoSaMP:iterative signal recovery from incomplete and inaccurate samples[J].Applied and Computational Harmonic Analysis，2009(26):301-321.

[18]DONOHO D，TSAIG Y，DRORI I，et al.Sparse solution of underdetermined linear equations by stagewise orthogonal matching pursuit[EB/OL].[2012-09-22].http://citeseerx.ist.psu.edu/viewdoc/versions?doi=10.1.1.115.5221.

[19]DO T，GAN L，NGUYEN N，et al.Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]//Proc.the 42th Asilomar Conference on Signals，Systems and Computers.Pacific Grove，California:IEEE Press，2008:581-587.

[20]BLUMENSATH T，DAVIES E.Iterative thresholding for sparse approximations[J].Journal of Fourier Analysis and Applications，2008，14(5):629-654.

[21]BLUMENSATH T，DAVIES E.Iterative thresholding for compressed sensing[J].Applied and Computational Harmonic Analysis，2009，27(3):265-274.

[22]MUN S，FOWLER J.Block compressed sensing of images using directional transforms[C]//Proc.International Conference on Image Processing.Cario，Egypt:IEEE Press，2009:3021-3024.

[23]CHEN C，TRAMEL E，FOWLER J.Compressed-sensing recovery of images and video using multihypothesis predictions[C]//Proc.Conference Record of the Forty Fifth Asilomar.Pacific Grove，CA:IEEE Press，2011:1193-1198.

[24]JI S，XUE Y，CARIN L.Bayesian compressive sensing[J].IEEE Trans.Signal Processing，2008(56):2346-2356.

[25]BABACAN S，MOLINA R.Bayesian compressive sensing using Laplace priors[J].IEEE Trans.Image Processing，2010，19(1):53-63

[26]BARON D，SARVOTHAM S，BARANIUK R.Bayesian compressive sensing via belief propagation[J].IEEE Trans.Signal Processing，2010，58(1):269-280.

[27]TIPPING M.Bayesian inference:an introduction to principles and practice in machine learning[EB/OL].[2012-10-29].http://www.miketipping.com/papers.htm.

[28]TIPPING M.Sparse bayesian learning and the relevance vector machine[J].The Journal of Machine Learning Research，2001(1):211-244.

[29]CANDES E，ROMBERG J.Sparsity and incorhence in compressive sampling[J].Inverse Problems，2007(23):969-985.

[30]CANDES E，TAO T.Decoding by linear programming[J].IEEE Trans.Information Theory，2005，51(12):4203-4215.

[31]DONOHO D，ELAD M.Optimally sparse representation in general(nonorthogonal)dictionaries vis l1 minimization[C]//Proc.Nationsl Academy of Sciences.Pacific Grove，California:IEEE Press，2003:2197-2202.

[32]BARANIUK R，DAVENPORT M，DEVORE R，et al.A simple proof of the restricted isometry property for random matrices[J].Constructive Approximation，2008，28(3):253-263.

[33]MENDELSON S，PAJOR A，TOMCZAK-JAEGERMANN N.Uniform uncertainty principle for bernoulli and sub-gaussian ensembles[J].Constructive Approximation，2008，28(3):277-289.

[34]BARON D，DUARTE M，WAKIN M，et al.Distributed compressive sensing[EB/OL].[2012-10-29].http://www.arxiv.org/abs/0901.3403.

[35]CANDES E，TAO T.Near optimal signal recovery from random projections:universal encoding strategies?[J].IEEE Trans.Information Theory，2006，52(12):5406-5425.

[36]DUARTE M，WAKIN M，BARANIUK R.Fast reconstruction of piecewise smooth signals from incoherent projections[C]//Proc.Workshop of Signal Processing Adaptive Sparse Structure Representation.Pacific Grove，CA:IEEE Press，2005:102-112.

[37]GAN L，DO T，TRAN T.Fast compressive imaging using scrambled block hadamard ensemble[C]//Proc.European Signal Processing Conference.Lausannne，Switzerland:IEEE Press，2008:1-5.

[38]MARSAGLIA G，BRAY T.A convenient method for generation normal variables[J].SIAM Review，1964，6(3):260-264.

[39]潘榕，段继忠，刘昱.压缩感知及其在图像和视频编码中的应用[J].电视技术，2012，36(1):10-14.

[40]张建新，刘郁林，张波，等.压缩感知在传感器网络中的应用研究[J].电视技术，2012，36(7):64-67.

[41]BARANIUK R，CEVHER V，DUARTE M，et al.Model-based compressive sensing[J].IEEE Trans.Information Theory，2010，56(4):1982-2001.

[42]练秋生，王艳.基于双树小波通用隐马尔可夫树模型的图像压缩感知[J].电子与信息学报，2010，32(10):2301-2306.

[43]EGIAZARIAN K，FOI A，KATKOVNIK V.Compressed sensing image reconstruction via recursive spatially adaptive filtering[C]//Proc.the International Conference on Image Processing.San Antonio，TX:IEEE Press，2007:549-552.