DTMB系统中BCH译码算法及其FPGA实现

吴子静，苏凯雄

(福州大学物理与信息工程学院，福建 福州 350002)

BCH(Bose，Chauhuri and Hocquenghem)码是循环码中的一大子类，可以有效地纠正多个随机错误。A.Hocquenghem在1959年、R.C.Bose和 D.K.Chaudhuri在1960年分别提出了二进制BCH码。Peterson在1960年证明了BCH码的循环结构。Gorenstein和Zierler在1961年将二进制BCH码推广到多进制［1］。BCH码的基本特征是其生成多项式g(x)包含2t个连续幂次的根，这使其具有不同于一般循环码的编译码算法，实现相对简单。从20世纪70年代起，BCH码便成为了线性分组码的主流。在现代通信的信道编码中，BCH码通常被用作级联码的外码，可以有效地消除内码的误码平台。如欧洲的第二代数字视频广播标准 DVB－S2、DVB－C2、DVB－T2 及我国的数字电视地面广播标准DTMB都采用了BCH码作为外码、LDPC码作为内码的信道编码方案。

BCH码最经典、最通用的译码算法是伯利坎普(Berlekamp)迭代译码 +钱氏搜索法［1－5］，该算法适用于各种纠错能力、多进制的BCH码的译码。由于DTMB标准中采用的是缩短的二进制BCH码，且纠错能力是1，故本文根据该BCH码的特性，提出一种更简单的BCH码译码算法，并设计出基于FPGA的BCH译码器。其硬件复杂度低、资源占用少、译码时延小。

1 传统BCH码的译码算法

BCH的译码算法比编码算法复杂得多，由于它是线性分组码，故其最基本的思路与一般的线性分组码类似:

1)由接收到的码字r(X)计算校正子S(X);

2)根据校正子S(X)找出错误图样e(X);

3)计算c(X)=r(X)－e(X)，得到译码器的估值码字。

又由于BCH码连续幂次根的性质，为它的译码带来了特殊算法，其中最经典最通用的是伯利坎普迭代译码+钱氏搜索法，具体有如下几个步骤:

1)校正子S(X)的计算

首先，用接收到的码字r(X)分别除以2t个根αi所对应的最小多项式mi(X)，得到2t个余式bi(X)，其中i=1，2，…，2t。由于 r(X)=ai(X)mi(X)+bi(X) ，且有mi(αi)=0，可得校正子的分量为

由于Si=r(αi)=c(αi)+e(αi)=e(αi) ，故求出校正子便可以进一步求出错误图样，从而完成译码。

2)错误图样e(X)的计算

错误图样由错误位置和错误值决定，对于二进制BCH码而言，其错误值为1，只需求出错误位置。若一个码字中共有 v(0≤v≤t) 个错误，令j1，j2，…，jv，(0≤jv≤n)表示错误的位置。则错误图样和校正子分量分别为

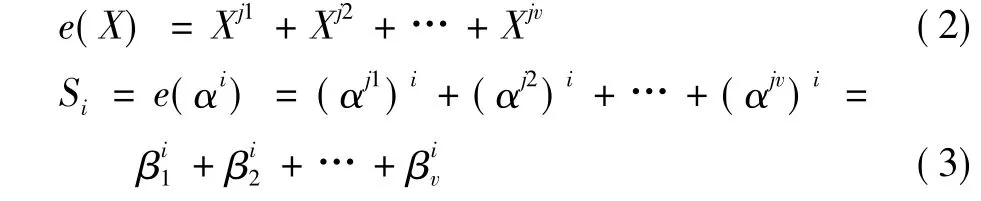
式中:βl=αjl，称为错误位置数。若求出错误位置数，则其幂次就是错误的位置。

错误图样有很多组解，其中具有最小错误数的错误模式就是正确的解。定义了一个错误位置多项式

该多项式的根是错误位置数的倒数。

因此，求错误图样具体分为以下2个步骤:

(1)用伯利坎普迭代算法求错误位置多项式

错误多项式的系数可以由伯利坎普迭代算法求得。迭代的第1步是求最低次数多项式σ(1)(X)，使它的系数满足第1个牛顿恒等式。第2步是检验σ(1)(X)的系数是否也满足第2个牛顿恒等式。若满足，则取σ(2)(X)=σ(1)(X)。若不满足，则对σ(1)(X)增加一个修正项构成σ(2)(X)，使σ(2)(X)满足前两个牛顿恒等式。如此迭代下去，得到σ(2t)(X)为止，即为错误位置多项式。

(2)用钱氏搜索算法求错误位置

首先，计算错误位置多项式的根。将 1，α，α2，…，αn－1代入σ(X)，若σ(αl)=0，则αl为它的根。那么，错误位置数为其根的倒数，即βl=αn－l，则错误位置为n－l。钱闻天提出了著名的钱氏搜索算法，从工程上解决了此问题，成为求取σ(X)的根的标准算法。即对码的每个位置逐位检验来确定其错误位置，从最高位rn－1开始译码。译第rn－l位码时，译码器检验 αn－l是否为错误位置数，也就是检验它的倒数αl是否为σ(X)的根。若αl是根，则1+ σ1αl+ σ2α2l+… + σvαvl=0，即该位码是错误的，否则是正确的。

3)计算c(X)=r(X)－e(X)得到译码器的估值码字

从以上步骤可以看出，传统的二进制BCH码译码算法虽然适用于各种纠错能力的BCH码，但译码过程比较复杂，特别是错误位置多项式与错误位置的求取最为繁琐，电路实现复杂度高、译码时延较长。在实际工程应用中往往采用的是纠错能力不那么强的BCH码，故本文以DTMB标准中的BCH码为研究对象，提出比传统译码算法更简单的BCH码译码算法和实现电路。

2 适用于DTMB标准的BCH译码算法

2.1 DTMB标准中的BCH码

我国数字电视地面广播国家标准(DTMB)中，输入的比特码率经过PN序列加扰后，接着进行前向纠错编码。前向纠错编码是由外码(BCH)和内码(LDPC)级联实现的。其BCH(762，752)是由 BCH(1023 ，1013 )系统码缩短而成的［6］。在 752 bit数据扰乱码前添加261 bit“0”形成 1013 bit，编码成 1023 bit。然后去除前261 bit“0”，形成762 bit BCH码字。该BCH码的生成多项式为

二进制本原 BCH(n，k，t)码满足

式中:n为码长;k为信息位长度;t为纠错能力;dmin为码的最小距离。根据式(6)，可以得到BCH(1023 ，1013 )中m=10，纠错能力 t=1。

BCH码的生成多项式由它在伽罗华域GF(2m)上的根确定。令α为GF(2m)的本原，2t个连续幂次根α，α2，…，α2t所对应的二元域上的最小多项式为m1(x)，m2(x)，…，m2t(x)，则纠t个错误的BCH码的生成多项式为这些多项式的最小公倍数，即

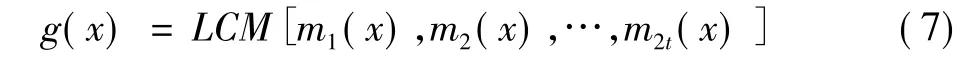
由于α的每个偶次幂都与其前面的每个奇数幂具有相同的最小多项式，因此有

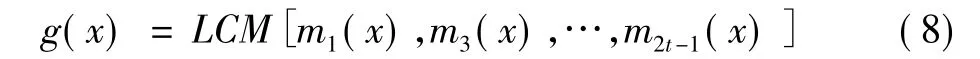
根据式(8)，可得纠单个错误的BCH码的生成多项式为

由于α是GF(2m)的本原，故m1(x)是m次本原多项式。因此可得码长为2m－1，纠单个错误的BCH码是循环汉明码。即可以把DTMB标准中的BCH(1023 ，1013 )码看作是纠错能力为1的循环汉明码。

2.2 DTMB标准中BCH码的译码算法

通过上述分析，已经证明了DTMB标准中的BCH码是循环汉明码。循环汉明码的译码过程与一般线性码相同，需要3个步骤，但实现方式不同。

1)校正子的计算

对于循环码，其校正子的计算公式为

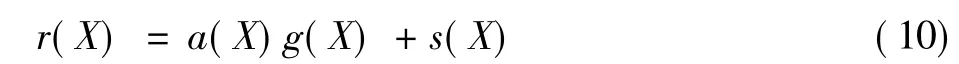
式中:r(X)为接收到的序列，表示为r(X)=r0+r1X+…+rn－1Xn－1;g(X)为生成多项式;s(X) 为校正子。即用r(X)除以g(X)，得到的余式就是s(X)。这可以用一个除法电路来计算它的校正子，这个电路的复杂度线性正比于校验位的数目，即n－k。若校正子为0，则表示接收的码字是正确的，否则是错误的。

2)由校正子检测错误模式

循环码的循环结构可以对接收序列r(X)进行串行译码，每次只译1位接收码，且每一位数据可以使用相同的电路进行译码。首先对r(X)的最高位Xn－1进行译码，即错误多项式为

若单个错误发生在最高位，则其校正子为Xn－1/g(x)的余式;若单个错误发生在其他位置上，则校正子不相同。因此，仅需一个m输入的异或门，就可以检测出该校正子的图样。若单个错误不是发生在最高位，则将接收多项式r(X)和校正子同时循环移位1位。这样便得到r(1)(X)=rn－1+r0X+ … +rn－2Xn－1，及 r(1)(X) 的校正子S(1)(X)。此时r(X)的第2位变为r(1)(X)的第1位，使用同样的检测电路，便可检测S(1)(X)是否与Xn－1位存在差错的错误模式相对应。以此类推，便可完成对所有位的检测。

3)差错纠正

若检测出r(X)的校正子S(X)与Xn－1位的错误模式相对应，则rn－1为差错位。可以通过式(12)纠正，即

同时将错误模式与校正子模2加，消除差错位en－1对校正子的影响。

从以上步骤可以看出，该算法与传统译码算法最大的差别在于错误模式(图样)的检测上。该算法错误模式的计算简单，且错误模式的检测电路只需一个m输入的异或门即可实现，极大地简化了译码过程，降低了电路的复杂度。

3 BCH译码算法的FPGA实现

3.1 BCH码串行译码器的实现

根据上述的译码算法，可以设计出相应的译码电路，主要由3个部分组成:校正子寄存器、错误模式检测器和存储接收向量的缓冲寄存器。为消除错误对校正子的影响，需将差错位通过一个异或门反馈到校正子移位寄存器。译码器工作原理如下［1］:

1)接收向量全部移入校正寄存器得到校正子，同时接收向量存入到缓冲寄存器中。

2)将校正子读入检测器中，检测相应的错误模式。检测器为组合逻辑电路，当且仅当校正子寄存器中的校正子所对应的接收向量的最高位存在差错时，输出为1。

3)从缓冲寄存器中读取第1个接收符号，并将校正子寄存器移位1次。若检测到第1个接收符号存在差错，则被检测器的输出纠正，同时e(X)=Xn－1的校正子被反馈回校正子寄存器来修正校正子。

4)接着对第2个接收符号(此时处于缓冲寄存器的第1位)进行译码。译码器重复步骤2)～3)。

5)译码器按以上步骤对接收到的符号逐位译码，直到从缓冲寄存器读出整个接收序列为止。

BCH码译码器的实现电路如图1所示。图中，接收码字r(X)是从校正子寄存器右端输入的，等价于错误多项式预先移位m位，即需要修改差错检测电路。若单个错误发生在最高位，则其校正子为Xm·Xn－1/g(x)的余式。

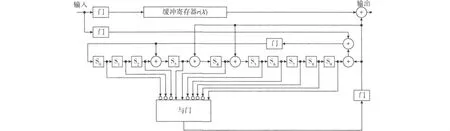
图1 BCH码串行译码器

对于BCH(1023 ，1013 )码，可计算得其校正子应为X10·X1023－1/g(x) 的余式，即

用一个与门便可检测校正子图样(0，0，0，0，0，0，0，0，0，1)，与门输入端为 s'0，s'1，…，s'm－2和 sm－1。其中 si为校正子，s'i为si的取反。

另外，DTMB标准中，BCH码是缩短的循环码，信息位中前261位为0，故在计算校正子时，不影响校正子最后的值，可以省去，故校正子的计算只需762个时钟。但对应的检测电路是从最高位r1022开始检测并输出。之后的261位都为0，并且是无用的信息。为了避免这额外的校正子寄存器的261次移位，需修改原先的差错检测电路。第r761位对应的校正子为X10·X1023－261－1/g(x)的余式，即

校正子图样为(0，0，0，1，1，0，0，0，0，1)，与门输入端为 s'0，s'1，s'2，s3，s4，s'5，s'6，s'7，s'8，s9。

图2为BCH码串行译码的ModelSim波形仿真图。

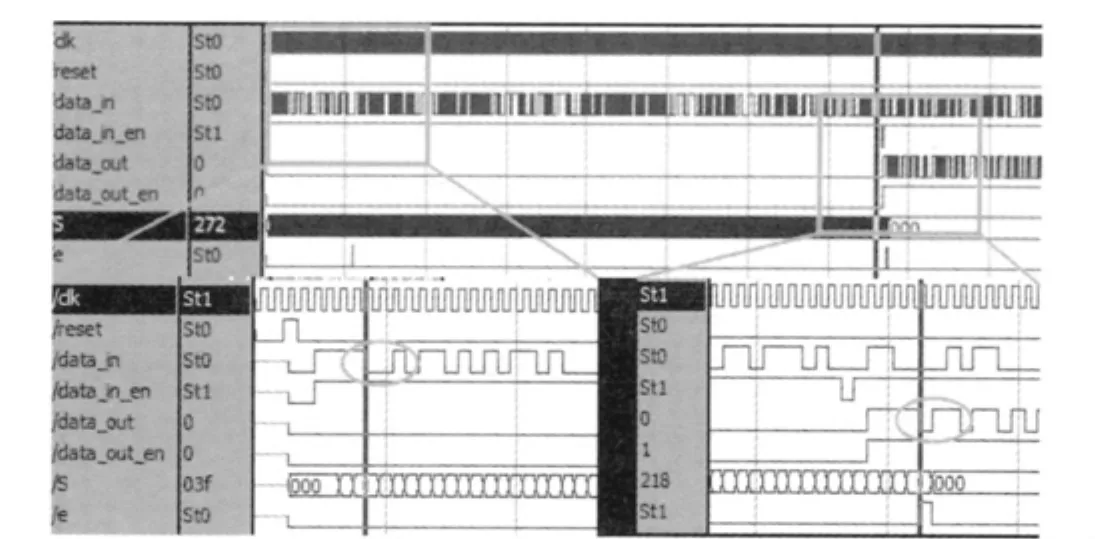
图2 BCH码串行译码ModelSim波形仿真(截图)

从图2中可以看到，译码器输入的第5位为0，输出为1，该差错已被译码器纠正，译码的结果是正确的。一个完整的译码从完全输入到开始输出有762个时钟的延时。采用Altera的Stratix II系列EP2S90F1020C4平台进行综合，综合结果表明该译码器仅占用48个ALUT逻辑单元，资源消耗极小。

3.2 BCH码并行译码器的实现

为了满足系统速率的要求，本文在串行BCH译码器的基础上设计了BCH码并行译码器，实现10位的并行输入输出译码。本文首先在接收到的762位符号前补8位0，形成770位，再进行译码，输出也为770位，再将前8位的0丢弃。译码器电路的校正子单元与错误模式检测需要进行相应改变。校正子循环移位单元在每个时钟周期需得到串行译码中循环移位10次后的值。校正子可通过式(15)计算得到，即

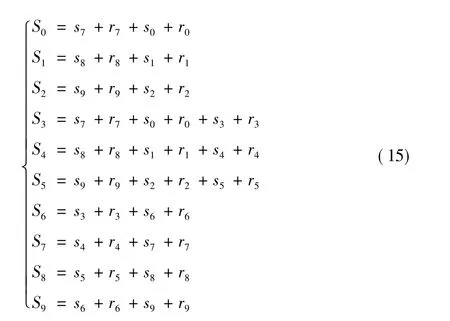
式中:Si为校正子寄存器的值;si为移位前寄存器中的值;ri为并行输入的第i个接收位。

另一个需要修改的部分是错误模式检测的组合逻辑单元。本文设计的是10位并行输出，需要设计10个组合逻辑单元来同时检测10位不同的错误模式，并进行纠正输出。计算 Xm·Xi－1/g(x) 的余式，其中 i=770，769，…，761，可得各个位置的组合逻辑检测电路为

若检测器输出ei为1，则ei(X)=X770+i的校正子将被反馈回校正子寄存器，通过模2加修正当前寄存器中的值。

图3为BCH码并行译码的ModelSim波形仿真图。

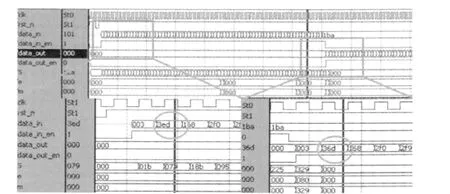
图3 BCH码并行译码ModelSim波形仿真(截图)

从图3中可以看出，译码器输入“3ED”已被纠正为“36D”(十六进制)，译码结果准确无误。一个完整的译码从完全输入到输出仅77个时钟的延时。在Altera的Stratix II系列EP2S90F1020C4平台的综合结果仅占用76个ALUT逻辑单元，资源占用极少。

4 结论

传统的BCH码的译码算法是伯利坎普迭代译码+钱氏搜索法，该算法虽然通用，但算法和硬件实现比较繁琐。本文研究了DTMB标准中的BCH码的特性，证明了该码是纠错能力为1的循环汉明码，提出了适用于该BCH码的译码方法，该方法比传统的BCH码的译码算法简单。并设计出两种译码电路:串行译码器和并行译码器。另外由于DTMB标准采用的是缩短的BCH码，在信息位前加上了261位的0，本文通过修改差错检测电路，使串行/并行译码器缩短了34%的译码时延，并行译码器的译码时延仅为77个时钟周期。该译码器硬件实现简单，FPGA的资源占用极少。

［1］LIN Shu，COSTELLO D J.Error control coding［M］.San Antonio:Pearson Education Inc.，2007.

［2］张博.数字电视传输系统中BCH码编/译码器的研究与FPGA实现［D］.北京:北京交通大学，2008.

［3］冯林浩.基于DTMB的纠错码译码器的研究与设计［D］.成都:电子科技大学，2010.

［4］许苑丰，王鹏.DTMB标准BCH译码器设计［J］.电子产品世界，2012，19(2):47－49.

［5］QIN Zhang，HU Qingsheng.Implementation of 10－Gb/s parallel BCH decoder based on Virtex－5 FPGA［J］.Advanced Materials Research，2012(429):159－164.

［6］GB20600—2006，数字电视地面广播传输系统帧结构、信道编码和调制［S］.2006.