多项交错级数敛散性的判定方法
2013-01-29蔺小林李仲博
蔺小林, 李仲博,2, 刘 侃,3
(1.陕西科技大学 电气与信息工程学院, 陕西 西安 710021; 2.陕西铜川工业技师学院, 陕西 铜川 727000; 3.陕西省商业学校, 陕西 汉中 723000)
0 引言
函数项级数是表示函数、研究函数性质以及进行数值计算的一种非常重要的工具.函数项级数特别是常数项级数的首要问题,就是敛散性的判断问题.我们知道常数项级数敛散性的判别问题是微积分中一个比较重要的问题[1].按照常数项级数收敛性的定义,把常数项级数敛散性转化为一个数列的敛散性问题,从而柯西判别准则给出了判断常数项级数收敛的充要条件, 一般来说它适应于一切常数项级数敛散性的判断.但是,要检测一个具体的常数项级数是否满足柯西判别准则的条件本身就不比检测这个级数是否收敛容易,因而一般在检测具体柯西判别准则级数是否收敛时, 使用柯西判别准则是有一定困难的, 有时甚至无法进行判断.特别对交错级数使用柯西判别准则往往失效.
莱布尼兹判别法是针对交错级数敛散性的有效判别准则.交错级数的莱布尼兹判别法在具体应用过程中也有以下问题,首先,判别法中的两个条件有时难于验证; 其次,在交错级数收敛时,不能直接判别级数是绝对收敛还是条件收敛;第三,莱布尼兹判别法只给出了交错级数什么时候收敛,而没有给出交错级数发散的条件,有些交错级数虽然不满足莱布尼兹判别法的条件,它也可能是收敛的级数.要得到对交错级数更多的非莱布尼兹型判别方法是比较困难的.文献[2-12]进行了推广并得到了一些比较好的结论, 但是对一个交错级数如何选取恰当的方法来判别它的敛散性仍是一个需要研究的问题.
从数学理论研究来看,还有比交错级数更普遍的多项交错级数以及广义交错级数,比如双项交错级数、k-项交错级数等等.对于这些更一般的交错级数,研究它们敛散性的判别准则具有重要意义.本文对多项交错级数以及广义交错级数的敛散性进行了讨论,把适用于交错级数的一些判别方法推广到多项交错级数以及广义交错级数上来,这些判别方法应用起来方便有效.
1 多项交错级数及其敛散性的概念
定义1.1 形如
(1.1)
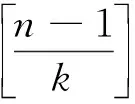
注1 当k=1时,就是一般意义下的交错级数[1];当k=2时,就是双项交错级数[2].
定义1.2 形如
a1+a2+…+am1
-am1+1-am1+2-…-am1+m2
+am1+m2+1+am1+m2+2+…+am1+m2+m3
-am1+m2+m3+1-am1+m2+m3+2-…-am1+m2+m3+m4
+……
(1.2)
的级数称为广义交错级数[13].
注2 当m1=m2=m3=…=k时,就是定义1.1的k-项交错级数[1].
定义1.3 记


a1+a2+…+am1+am1+1+am1+2+…+am1+m2
+am1+m2+1+am1+m2+2+…+am1+m2+m3
+am1+m2+m3+1+am1+m2+m3+2+…+am1+m2+m3+m4
+……
收敛,则称广义交错级数(1.2)绝对收敛.
2 多项交错级数及广义交错级数敛散性判定方法
定理2.1 若多项交错级数(1.1)满足
(2)a2mk+1+a2mk+2+…+a(2m+1)k-a(2m+1)k+1-…-a(2m+1)k+k=bm
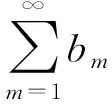
证明:见文献[3].
定理2.2 若多项交错级数(1.1)满足:
则多项交错级数(1.1)收敛,且和S满足0≤S≤a1+a2+…+ak.
证明:考虑多项交错级数(1.1)前2k(m+1)项的和,记
S2k(m+1)=a1+a2+…+ak
-ak+1-ak+2-…-a2k
+a2k+1+a2k+2+…+a3k
-a3k+1-a3k+2-…-a4k
+a2mk+1+a2mk+2+…+a(2m+1)k
-a(2m+1)k+1-a(2m+1)k+2-…-a(2m+1)k+k,
一方面,根据条件(1)有
S2k(m+1)= [a1+a2+…+ak
-(ak+1+ak+2+…+a2k)]
+[(a2k+1+a2k+2+…+a3k)
-(a3k+1+a3k+2+…+a4k)]
+[a2mk+1+a2mk+2+…+a(2m+1)k
-(a(2m+1)k+1+a(2m+1)k+2+…+a(2m+1)k+k)]>0
另一方面有
S2k(m+1)=a1+a2+…+ak
-(ak+1+ak+2+…+a2k)
+(a2k+1+a2k+2+…+a3k)
-(a3k+1+a3k+2+…+a4k)
+(a4k+1+a4k+2+…+a5k)
-…-
-(a(2m-1)k+1+a(2m-1)k+2+…+a2mk)
+(a2mk+1+a2mk+2+…+a(2m+1)k)
-(a(2m+1)k+1+a(2m+1)k+2+…+a(2m+1)k+k),
S2km+1=S2km+a2km+1,
S2km+2=S2km+1+a2km+2,
…,
S2km+k=S2km+k-1+a2km+k
所以,根据条件(2)有
…,

定理2.3 若广义交错级数(1.2)满足:
(1)am1+m2+…+mk-1+1+am1+m2+…+mk-1+2
+…+am1+m2+…+mk-1+mk≥
am1+m2+…+mk+1+am1+m2+…+mk+2
+…+am1+m2+…+mk+mk+1
(k=0,1,2,…)(规定m0=0);
则广义交错级数(1.2)收敛,且和S满足0≤S≤a1+a2+…+am1.
证明类似于定理2.1的证明,从略.
参照交错级数的相关证明,可得下述显然结论:
定理2.4 对多项交错级数(1.1),若记
Ak=a1+a2+…+ak,
A2k=ak+1+ak+2+…+a2k,…,
Amk=a(m-1)k+1+a(m-1)k+2+…+a(m-1)k+k,
推论2.1 对多项交错级数(1.1),若
(1)存在N,对任何m>N,都有Amk>A(m+1)k;
则多项交错级数(1.1)收敛.
同样,对广义交错级数(1.2),也有如下显然结论:
定理2.5 对广义交错级数(1.2),若记
Am1=a1+a2+…+am1,
Am1+m2=am1+1+am1+2+…+am1+m2,…,
定理2.6 若多项交错级数(1.1)满足:
(1)存在N,对任何n>N,都有an>an+1;
则多项交错级数(1.1)收敛.

S2k(m+1)= (a1+a2+…+ak)
-(ak+1+ak+2+…+a2k)
+(a2k+1+a2k+2+…+a3k)
-(a3k+1+a3k+2+…+a4k)
+…+
(a2mk+1+a2mk+2+…+a(2m+1)k)-
(a(2m+1)k+1+a(2m+1)k+2+…+a(2m+1)k+k)
而
S2k(m+1)=S2km+(a2km+1+a2km+2+…+a2km+k)
-(a2km+k+1+a2km+k+2+…+a2k(m+1))

S2km+1=S2km+a2km+1,
S2km+2=S2km+1+a2km+2,
…,
S2km+k=S2km+k-1+a2km+k,
由条件(2)知,
,…,

对广义交错级数(1.2),我们有类似于定理2.5的结论如下,省略证明.
定理2.7 若广义交错级数(1.2)满足:
(1)存在N,对任何n>N,都有an>an+1;
则广义交错级数(1.2)收敛.

(1)当ρ<1时,多项交错级数(1.1)或广义交错级数(1.2)绝对收敛;
(2)当ρ>1或ρ=+ ∞时,多项交错级数(1.1)或广义交错级数(1.2)发散.
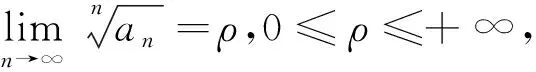
(1)当ρ<1时,多项交错级数(1.1)或广义交错级数(1.2)绝对收敛;
(2)当ρ>1或ρ=+ ∞时,多项交错级数(1.1)或广义交错级数(1.2)发散.
注在定理2.7和2.8中,当ρ=1时,多项交错级数(1.1)或广义交错级数(1.2)可能收敛,也可能发散.
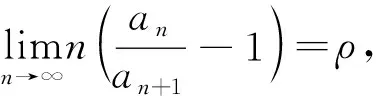
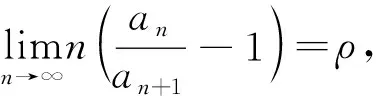
即
(2.1)
一方面,由于0<ε<ρ,显然有
另一方面,对(2.1)令n从N开始进行连乘到N+k,则有

所以

我们可以得到定理2.9的另外一种表示形式如下:

证明:仅对多项交错级数(1.1)的情形进行证明,对广义交错级数(1.2)的证明是类似的.
引理2.1[11](正项级数的Raabe 对数判别法)


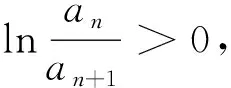
即
因而
故
从而
于是
>…>
即
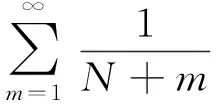
由定理2.6知l>0时级数(1.1)收敛.
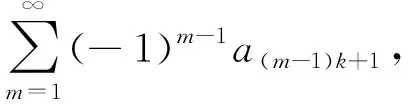

证明:(1)充分性 如果交错级数
都绝对收敛,即
都收敛,所以前n项和
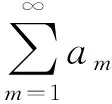


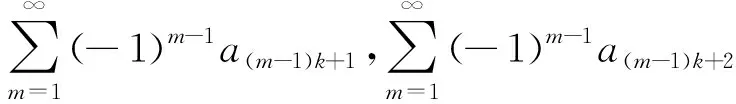
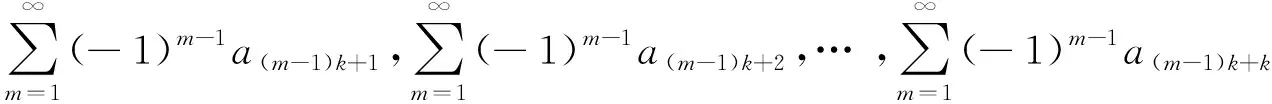
3 小结
我们对多项交错级数以及广义交错级数的敛散性进行了一些初步讨论,把适用于交错级数的一些判别方法推广到多项交错级数以及广义交错级数上来,这些判别方法仅仅是多项交错级数以及广义交错级数敛散性判别方法的一部分,还有必要进行更深入地研究,期待得到一些应用更加广泛,效果更好的判别方法.
[1] 同济大学数学教研室.高等数学(第五版)[M].北京:高等教育出版社,2009:258-260.
[2] 孙兰敏.张 平.双项交错级数敛散性的判定[J].衡水学院学报,2008,10(1):5-6,19.
[3] 范新华.关于交错级数敛散性判别法的一些探讨[J].常州工学院学报,2007,20(5): 57-59.
[4] 刘志高.交错级数的对数判别法[J].大学数学,2010,26(2):194-196.
[5] 王宣欣.交错级数敛散性的判别方法[J].山东广播电视大学学报,2010,16(2):66-67.
[6] 曾玉祥.交错级数敛散性的判别模式[J].成都大学学报(自然科学版),2008,27(4): 300-302.
[7] 钱伟懿.交错级数敛散性的一个新判别准则[J].高师理科学刊,2009,29(2):8-9,13.
[8] 郑玉敏.交错级数敛散性判别法[J].大学数学,2009,25(1):192-194.
[9] 刘晓玲.张艳霞.交错级数收敛性的一个判别法[J].高等数学研究,2007,10(1):51,53.
[10] 高德智,梁向前.数列的几乎单调性[J].高等数学研究,2008,11(3):17-19.
[11] 姬小龙,王 锐.正项级数的Raabe对数判别法[J].高等数学研究,2007,10(3):7-9.
[12] 蔺梦阳.交错级数比较和比值判别法探讨[J].陕西科技大学学报(自然科学版),2011,29(6):157-160, 192.
[13] 张洪光.莱布尼兹型级数的推广[J].赤峰学院学报(自然科学版),2010,26(2):9-10.
