发射药床初始堆积形态对破碎程度的影响

王 燕，芮筱亭，陈 涛，王国平

（1.南京理工大学发射动力学研究所，江苏 南京210094；2.南京理工大学力学实验中心，江苏 南京210094）

引 言

现代高性能火炮的高初速、高膛压、高装填密度特点，使得火炮膛内燃烧与力学环境越来越恶劣，发射安全性问题愈来愈突出。在相应的装药结构下发射装药破碎是导致膛内超高压力和膛炸的根本原因［1-3］，发射药床的破碎程度是评判发射安全性的关键参数。发射药床由发射药颗粒组成，药床的初始堆积形态千变万化，在相同的条件下，药床的初始堆积会导致膛内压力异常，从而导致膛炸等危险性事故的发生。姜世平等人［4-5］计算了相同的冲击载荷下不同初始堆积发射药床的破碎程度，结果表明，发射药床的初始堆积构型对其破碎程度有一定的影响，发射药床的初始堆积决定了发射药粒之间的受力关系及其破坏形式。周彦煌等人［6］用空气炮对发射药床进行挤压和撞击破碎试验，研究了发射药床在横排与竖排堆积形态下的破碎情况。金志明等人［7］对单颗发射药及火药床进行了动态挤压试验，但未考虑初始堆积形态对破碎程度的影响。芮筱亭、冯宾宾、徐浩等人［8-9］用发射装药动态挤压破碎装置对某硝胺发射药进行了发射药破碎规律研究。

本研究采用发射装药动态挤压破碎试验装置研究了发射药床不同初始堆积形态对其破碎程度的影响，并通过发射装药破碎程度表征试验［10-11］，获得了相应条件下破碎发射药床的起始动态活度比。

1 发射药床堆积形态

发射药床由两种粒状发射药组成，两种发射药的形状均为梅花形19孔药，组分相同。小药粒弧厚为1.49mm，大药粒弧厚为1.69mm。

发射药床质量均为150g，对不同初始堆积形态的发射药床进行编号，分别从1至10，发射药床的高度（h）见表1，随机、竖排和横排堆积的发射药床如图1所示。由表1可得，发射药床的随机堆积高度最低34.51mm、最高35.06mm，平均高度为34.81mm，最大相对误差为0.87%；竖排药床高度小于随机堆积高度，横排药床高度与随机堆积较接近。

图1 3种堆积形态的发射药床Fig.1 Propellant beds of three kinds of packing patterns

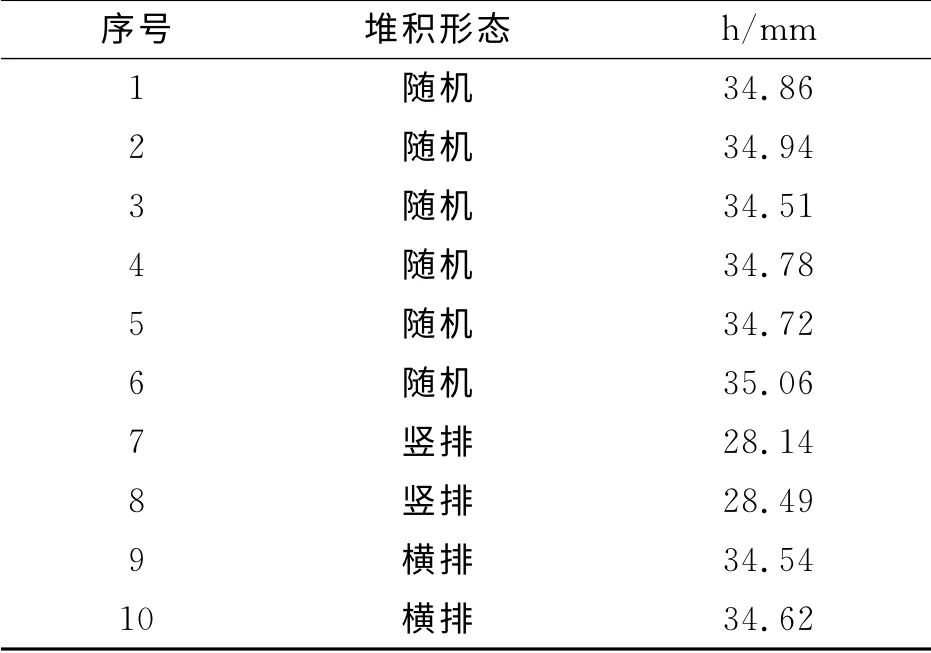
表1 发射药床高度Table 1 Height of propellant beds

2 发射装药动态挤压破碎试验

发射装药动态挤压破碎试验原理图如图2 所示。在燃烧室中加入火药，燃烧后生成的高压气体推动活塞，高速运动的活塞快速挤压装药室内的发射装药。该装置模拟了火炮发射过程中弹底发射装药的挤压破碎过程，获得破碎的发射药。

图2 发射装药动态挤压破碎试验装置Fig.2 Dynamic compression fracture device of propellant charge

为了研究发射药床的初始堆积形态对破碎程度的影响，依次对1～10号发射药床进行动态挤压破碎试验。由于火炮膛炸、早炸等事故常发生在低温情况下，试验前先将发射药床保温至-40℃，保温12h。除了发射药床的初始堆积形态不同，燃烧室内的火药量、活塞的限定位移都相同。图3为发射药床不同堆积形态与燃烧室压力之间的关系。由图3可见，三条曲线的最大值和上升趋势基本一致，说明在试验过程中不同堆积形态的药床所受的冲击载荷一致。图4为发射药床动态挤压破碎试验后的破碎发射药照片，可见竖排堆积发射药床的破碎程度明显小于其他两种堆积形态。横排堆积的发射药床部分已破碎成粉末状。

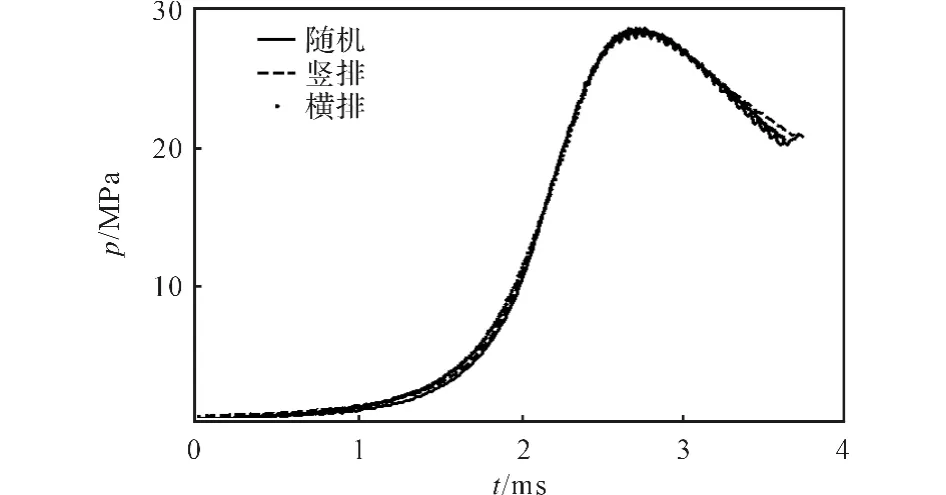
图3 发射药床堆积形态与燃烧室压力之间的关系Fig.3 Relation between pressures in burner and propellant bed packing patterns

图4 药床挤压后的破碎药粒照片Fig.4 Photos of fragmented propellant grains after compression

3 发射药床破碎程度的表征

3.1 发射药床破碎程度表征方法

发射药动态活度的定义如下［10］：

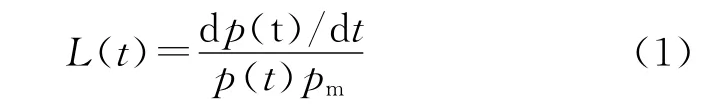
根据发射装药在密闭爆发器内燃气状态方程：

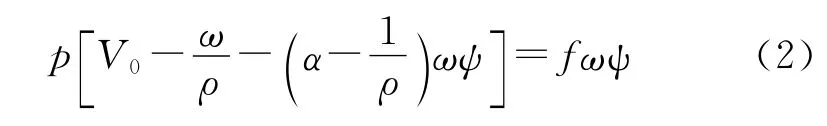
通过等式两边求导以及发射药形状函数等方程，式（1）可写成：

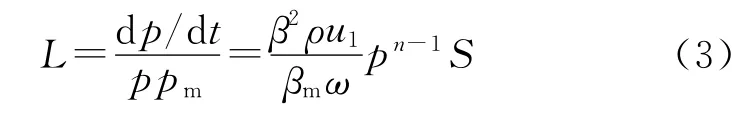
根据发射装药动态活度比的定义［10］：

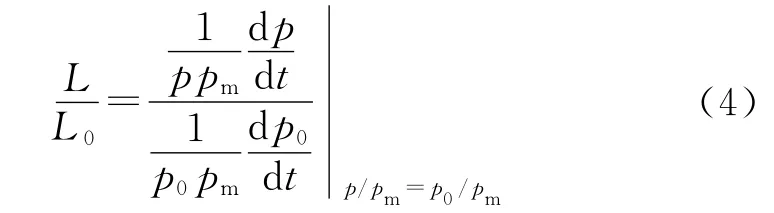
式中：L为破碎发射装药动态活度；L0为未破碎发射装药动态活度；下标“0”表示未破碎发射装药。

在相同装药条件下，发射药的u1、ω、ρ相同，密闭爆发器内最大压力pm也相同。在对应相同p／pm值的瞬时压力p0与p相等，式（4）可写为：

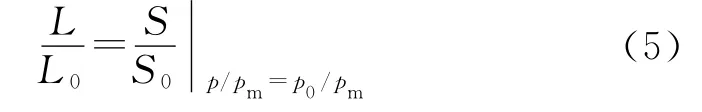
由式（5）可知，发射装药的动态活度比等于破碎发射装药与相应未破碎发射装药的燃烧表面积之比。

3.2 发射药床破碎程度表征试验

发射药破碎程度的表征系统［11］如图5所示，由密闭爆发器、测压传感器、信号放大器、数据采集系统、点火装置以及数值处理系统等组成。密闭爆发器中发射药的装填密度为0.2g／cm3，发射药量为150g。硝化棉作点火药，试验温度为（20±1）℃。分别对未破碎发射药床和破碎发射药床进行密闭爆发器试验，p-t曲线如图6所示，压力曲线0为未破碎发射药床。由图6可以看出，各发试验的压力最大值基本一致，未破碎发射药床的燃烧时间较长，破碎发射药床的燃烧时间较短，且横排堆积破碎发射药床的燃烧最快。

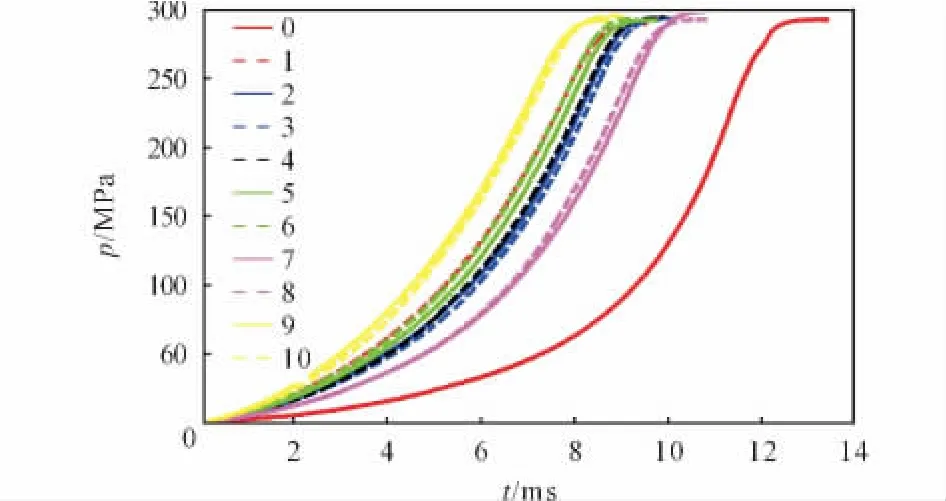
图6 发射药床的p-t曲线Fig.6 The p-t curves of propellant beds

根据公式（1）用测试获得的p-t曲线得到发射药床的动态活度曲线见图7，由公式（3）可知，动态活度L反映了发射药床的燃烧面积。压力上升越缓慢，在p／pm在0.2～0.8之间，动态活度L下降越缓慢，说明发射药床的燃烧面积减小较缓慢。

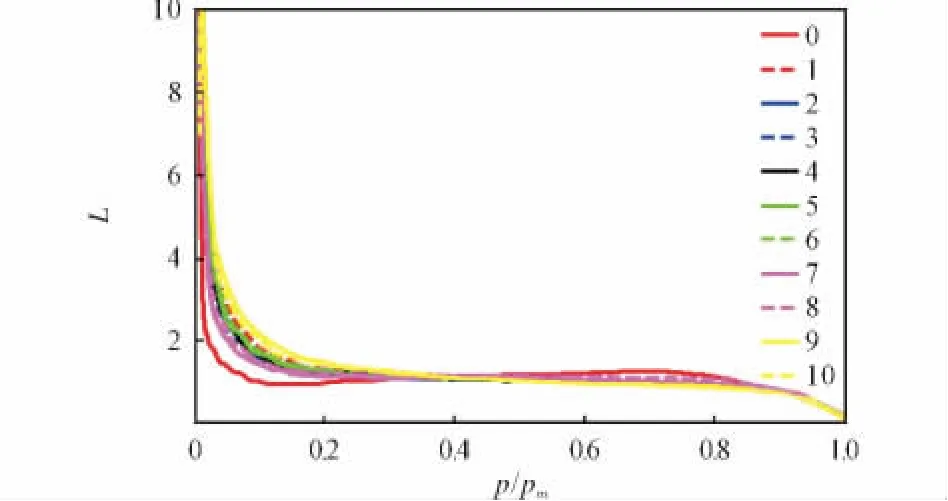
图7 发射药床动态活度曲线Fig.7 Dynamic vivacity curves of propellant beds

利用公式（4），可计算挤压破碎后发射药床的动态活度比，拟合曲线如图8所示。在图8曲线上，以0.1为步长，在p／pm为0.2～0.8上取点，用最小二乘法拟合直线，拟合直线与纵坐标轴的截距即为起始动态活度比。图9为通过最小二乘法拟合动态活度比曲线的拟合直线以及起始动态活度比。由图9可以得到起始动态活度比大小关系：竖排堆积＜随机堆积＜横排排堆积，说明横排堆积的发射药床破碎最严重，这与通过动态挤压破碎试验观察的情况相一致。

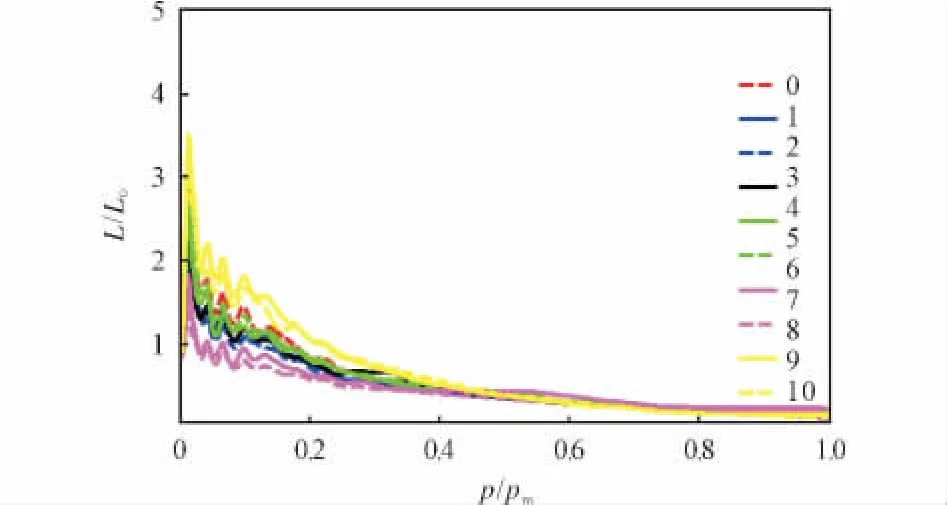
图8 破碎发射药床动态活度比曲线Fig.8 Dynamic vivacity ratio curves of fragmented propellants

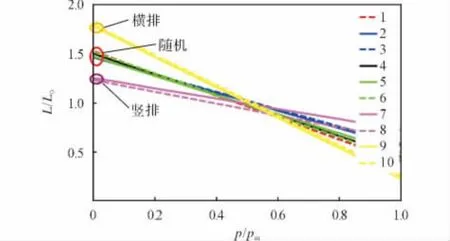
图9 破碎发射药床的起始动态活度比拟合曲线Fig.9 Fitting curves of initial dynamic vivacity ratio of fragmented propellants

表2为破碎发射药床的起始动态活度比。由表2可知，随机堆积发射药床的起始动态活度比的最大值为1.530，最小值为1.467，平均值为1.495，最大相对误差仅为2.34%，这说明试验中随机堆积的发射药床破碎一致性较好；随机堆积的发射药床起始动态活度比明显小于横排堆积，但大于竖排堆积，说明在相同冲击载荷的情况下横排堆积的发射药床易破碎。

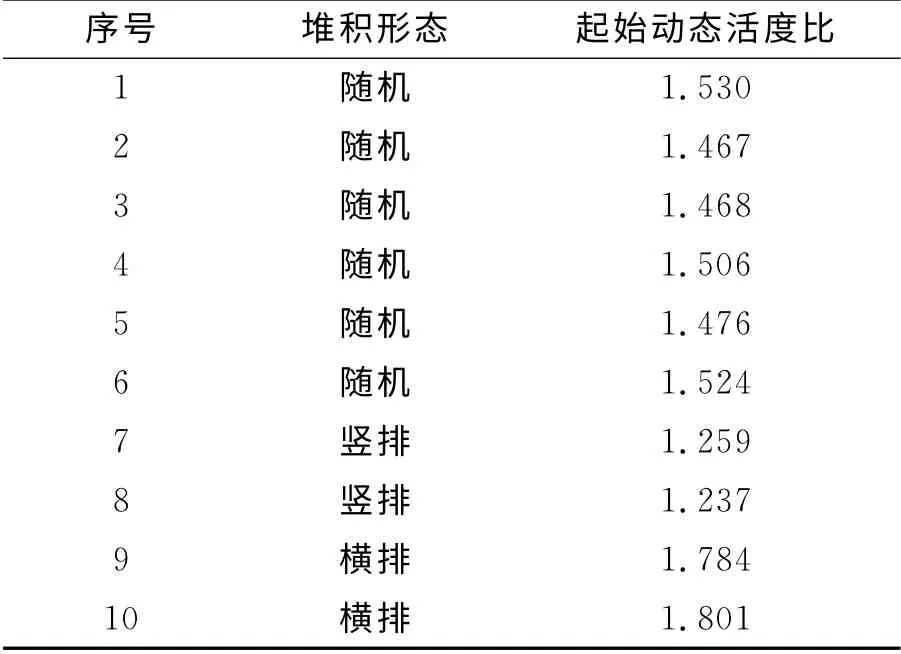
表2 破碎发射药床的起始动态活度比Table 2 Initial dynamic vivacity ratios of fragmented propellants

4 结 论

（1）发射药随机堆积时，在相同的冲击载荷下，其破碎程度一致，因此试验时无需对发射药的初始堆积进行特殊处理。

（2）发射药为竖排或横排堆积时，在相同的冲击载荷下，其破碎程度有较大的差异。横排堆积的发射药床更易破碎，发射药床的初始表面积最大，因而其起始动态活度比也最大。

［1］Gazanas G A.Mechanical response of M30，XM39and JA2propellant at strain rate from 10-2to 250s-1，ADA231 435／9／GAR［R］.Springfield：NTIS，1991.

［2］Horst A W，May I W，Clarke E V.The missing link between pressure waves and breechblows，AD-A058 354／2GA［R］.Springfield：NTIS，1978.

［3］Keller G E，Horst A W.Effects of propellant grain fracture on the interior ballistics of guns，AD-A209 007／4／GAR［R］.Springfield：NTIS，1989.

［4］姜世平.散体系统破碎动力学研究［D］.南京：南京理工大学，2011.

JIANG Shi-ping.Study on fracture dynamics of granular matter［D］.Nanjing：Nanjing University of Science and Technology，2011.

［5］JIANG Shi-ping，RUI Xiao-ting，HONG Jun，et al.Numerical simulation of impact breakage of gun propellant charge［J］.Granular Matter，2011，13：611-622.

［6］周彦煌，张明安，刘千里.炮用发射药动态破碎试验方法及破碎现象的观察［J］.弹道学报，1990（1）：59-67，12.

ZHOU Yan-huang，ZHANG Ming-an，LIU Qian-li.An experiment method and phenomenon observation of dynaic fragmcnting for gun propellants［J］.Journal of Ballistics，1990，1：59-67，12.

［7］金志明，翁春生.高等内弹道学［M］.北京：高等教育出版社，2003.

［8］冯宾宾，芮筱亭，徐浩，等.发射过程中某硝胺发射装药的动态挤压破碎情况［J］.火炸药学报，2012，35（2）：70-73，85.

FENG Bin-bin，RUI Xiao-ting，XU Hao，et al.Dy-namic compresion fracture condition of one nitroamine propellant charge during launch course［J］.Chinese Journal of Explosives and Propellants，2012，，35（2）：70-73，85.

［9］徐浩，芮筱亭，郁兆华，等.发射装药挤压应力与破碎规律研究［J］.火炸药学报，2012，35（4）：61-64.

XU Hao，RUI Xiao-ting，YU Zhao-hua，et al.Study on extrusion stress and fracture law of propellant charge［J］.Chinese Journal of Explosives and Propellants，2012，35（4）：61-64.

［10］芮筱亭，贠来峰，王国平，等.弹药发射安全性导论［M］.北京：国防工业出版社，2009.

［11］陈涛，芮筱亭，贠来峰.发射药破碎程度描述方法［J］.弹道学报，2008，20（2）：99-102.

CHEN Tao，RUI Xiao-ting，YUN Lai-feng.Method of describing fracture degree of propellant［J］.Journal of Ballistics，2008，20（2）：99-102.