基于f－散度的一致风险度量

任凤英， 李兴斯

（1.大连理工大学运筹学与控制论研究所，辽宁大连 116024；2.北京师范大学珠海分校应用数学学院，广东珠海 519087）

基于f－散度的一致风险度量

任凤英＊1，2， 李兴斯1

（1.大连理工大学运筹学与控制论研究所，辽宁大连 116024；2.北京师范大学珠海分校应用数学学院，广东珠海 519087）

进一步研究了带有熵约束的一致风险度量，鉴于它的许多良好性质，提出了带有f－散度约束的一致风险度量，获得了一大组可以灵活选取的风险度量，并且给出了一致风险度量理论中可接受集的控制方法.另外，讨论了将这类风险度量直接用于优化问题的优点以及它们的稳健化处理方法，得到了一致风险度量的新的表现形式，此形式是CVaR的上界，在应用中是更易处理的.

一致风险度量；凸风险度量；一致熵风险度量；一致f－散度风险度量

0 引 言

根据一致风险度量理论，对于一组风险资产构成的组合X，决策者能够知道需要多少资本储备，使得组合X的风险可以接受.其基本思想是首先定义一个可接受集合A，需要A满足一些合理的性质，这组性质形成风险度量的一致性公理，任何一个满足一致性公理的风险度量都可以表示为

这个表达式也称为一致风险度量的对偶表达式，其中Q∈Σ，Σ代表概率测度的集合，它的大小本质上是由可接受集合A决定的.因为要使风险X变得可以接受，那么所需的最小资本储备是ρ（X）＝｛m＋X∈A｝.集合A的大小决定了概率测度Q∈Σ的变化范围.如果知道如何说明可接受集A，就能构造相应的风险度量ρA（X）；反之，如果有一个一致风险度量ρ（X），就能表示出可接受集合＝｛X｜ρ（X）≤0｝.在文献［1］中，通过锥优化的对偶关系，说明了A与Σ的相互制约关系.由于定量地表达A是非常困难的，对于CVaR来说，可接受集合对应的概率测度集是Σ＝｛Q∈，其中M1是所有概率测度的集合.因此，有l－logα.受这一表达形式的启发，文献［1］提出在上面的风险度量的对偶表达式中，用相对熵（Kullback－Leibler散度）来控制Σ的大小，产生一个优化模型如下：

其中c由可接受的风险水平确定，通过控制参数c的变化来约束概率测度的集合，并对应不同的可接受集Ac，表示不同的代理人有不同的容忍度，同时也表示一组不同的风险度量ρc（X）.H（Q｜P）是Q关于P的相对熵，定义如下：

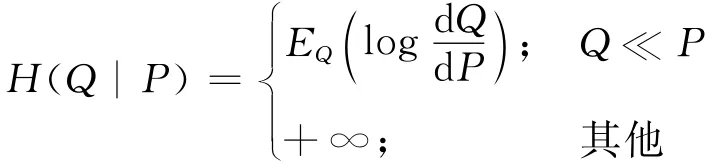
最近，Follmer等［2］从分布不变性、模型稳健性、独立风险聚合下的行为以及大偏差界等几个方面研究了一致风险度量的这种特殊形式，并称之为一致熵风险度量，记为

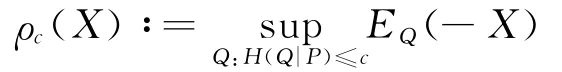
文献［2］是从凸熵风险度量的一致调整的角度来研究ρc（X）的性质的.凸熵风险度量的定义如下：

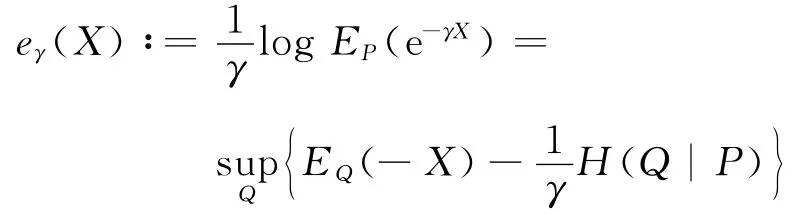
其中参数γ∈［0，＋∞），是风险厌恶系数.文献［2］分析了ρc（X）的一些性质，更多地侧重于这两个风险度量之间的差别.在精算问题中应用这两个风险度量时，ρc（X）比eγ（X）的表现更好.本文要在一致风险度量的统一表达式中，通过描述概率测度集合Σ，间接地表示各种不同的可接受集合A.除了相对熵外，也扩展到一般的f－散度，称之为一致f－散度风险度量.由于有一大组f－散度，产生了一组丰富的一致f－散度风险度量，并讨论它们的性质和应用问题.

1 记号与定义

设（Ω，F）为可测空间，X是定义在其上的有界可测随机变量的线性空间.让A表示可接受凸锥，Χ＋A且A∩（－A）＝｛0｝.那么泛函ρ（·）定义如下：

可接受集合A的性质导致ρ（X）有如下4条性质，称为一致性公理，即对于X，Y∈L∞和m∈R，λ∈R＋，有

（1）单调性：X≥Yρ（X）≤ρ（Y）

（2）平移不变性：ρ（X＋m）＝ρ（X）－m

（3）正齐性：ρ（λX）＝λρ（X）

（4）次可加性：ρ（X＋Y）≤ρ（X）＋ρ（Y）

满足这些性质的风险度量称为一致风险度量，它们有统一的对偶表达式：

当不要求有正齐性时，一致风险度量扩展为凸风险度量，它们的统一的对偶表达式为

其中Σ1表示在Χ上的所有概率测度，α（Q）定义如下：

当α（Q）∈｛0，＋∞｝时，凸风险度量的表达式化为一致风险度量的表达式［3－6］.

2 带约束的一致风险度量

2.1 一致熵风险度量

从引言的两个表达式可知，一致熵风险度量是带有Kullback－Leibler散度约束的风险度量；凸熵风险度量是带有熵罚的凸风险度量.

定义1对给定的c＞0，一致熵风险度量ρc定义如下：

其中Q∈Σ，Σ是一致风险度量定义中所有概率测度的集合.c的选取是为了控制概率测度集合Σ的大小.

ρc（X）的基本性质：

（1）对任何的α∈（0，1）和X∈L∞，

其中c（α）＝－logα＞0.

左边的不等式是已知的［2］，右边的不等式证明如下：

（3）根据ρc的定义，其中的最大值是可达的，即

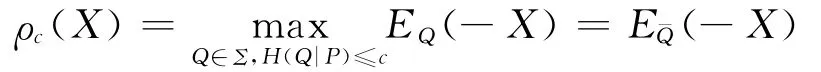
（4）当考虑n个不同的随机变量时，ρc有下面的性质：

这个性质说明：如果这n个随机变量表示n个保险合约，当合约数量增加时，每个合约的费用将下降到公平费用.性质（2）～（4）的证明见文献［2］.

2.2 一致f－散度风险度量

定义2 设概率测度Q关于P连续，f：（0，＋∞）→R是任意一个凸函数，使得f（1）＝0，那么Q和P之间的f－散度是

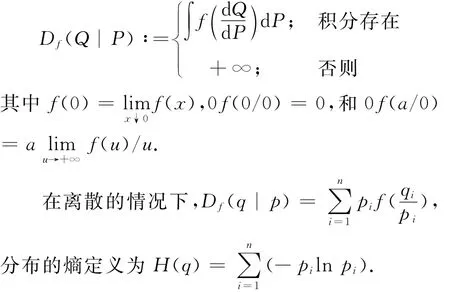
由于凸函数f可有多种选取方式，f－散度包含了一大组关于概率分布间距离的度量.另外，也会用到f的共轭函数f＊，定义如下：

下面是常用的凸函数及其代表的散度或称距离.

例1f（x）＝xlogx，对应Kullback－Leibler相对熵散度

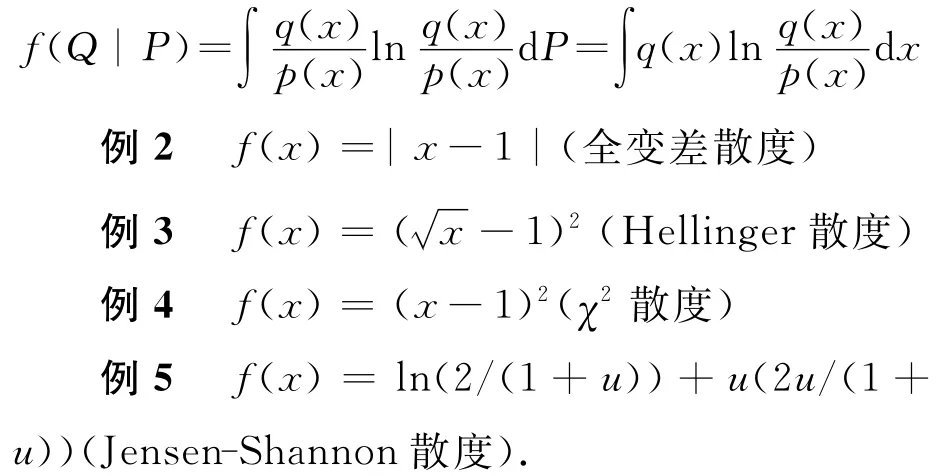
分布的熵与f－散度有密切的联系，如下面的式子：

已知的其他的散度还有很多，f－散度的一些基本性质如下：

性质1Df（Q｜P）＝Df＊（P｜Q）当且仅当屈c∈R：f＊（u）－f（u）＝c（u－1），f＊是f的伴随共轭函数.

性质2（Q｜P）＝Df（Q｜P），当且仅当屈c∈R：f1（u）－f（u）＝c（u－1）.

性质3f（1）≤Df（Q｜P）≤f（0）＋f＊（0）.

性质4Df（Q｜P）≥f（1）＝0，其中等式成立当且仅当Q＝P.

Q、P是任意的概率测度.

定义3对给定的c＞0，一致f－散度风险度量ρ（f，c）定义如下：

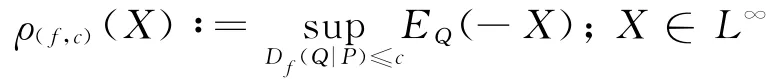
其中Q∈Σ，Σ是一致风险度量定义中所有概率测度的集合.显然一致熵风险度量是它的特例，将从优化的角度分析一致f－散度风险度量.它们的性质概括在下面的定理中.

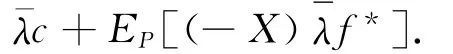
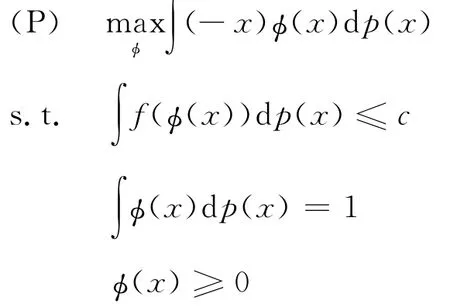
由于目标函数的线性和f的凸性，这是一个凸优化问题，使用Lagrange方法求解.

优化问题中的密度函数之比 （x）≥0，联系不等式的Lagrange乘子λ≥0.根据最优解的充分且必要条件，对所有的g（x），计算L关于g（x）的方向导数：

因此， （x）必须使下面的等式

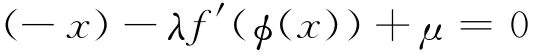
几乎处处成立.

（x）还需要满足下列约束条件和互补松弛条件：

可以断言λ＞0，否则，由最优性条件可推出x＝μ.这是退化的情况.当λ＞0，

当f（x）＝xlogx时， （x）＝e（－x）／λ＋μ／λ－1，最优值是可达的，记为

如果在优化问题中，默认 （x）是密度之比，则拉格朗日函数简化为

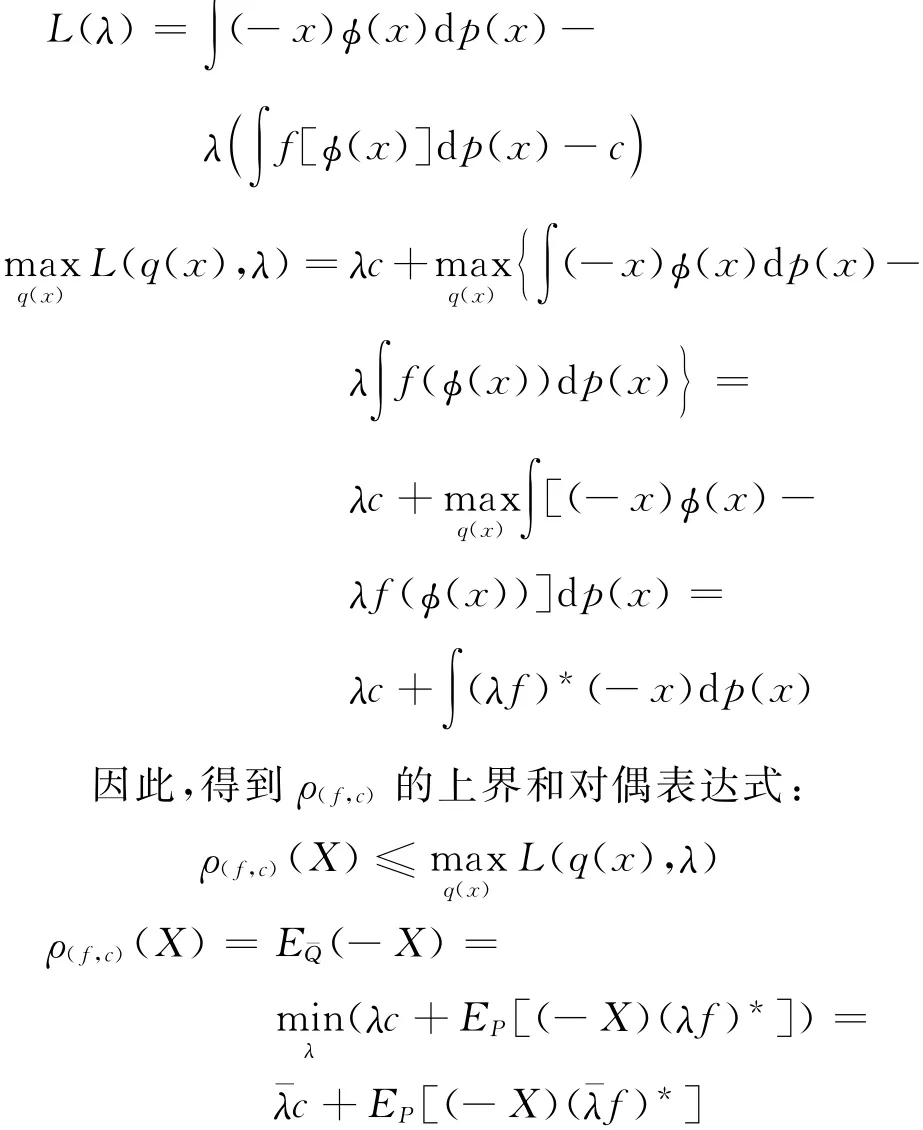
3 应 用

3.1 对冲问题中的应用

可以将一致f－散度风险度量融于对冲问题中，不必单独增加一个风险度量约束.一个风险最小化欧式期权对冲问题如下：

其中XT代表对冲组合在到期日的值，它由α份股票和β份无风险债券构成；CT是欧式期权在到期日的价值，暂且考虑单期的对冲问题.那么这个问题就是在可接受的风险容忍水平下，选取风险资产和无风险资产的投资组合，使得一致f－散度风险度量最小.所求得的最优值说明：还需要多少资本储备才能使得出售期权可能发生的负债在可接受的风险容忍水平之下.由于这个优化问题是一个凸优化，可以将其离散化后求解，它是在多项式时间内可解的［7］.

3.2 稳健化一致f－散度风险度量

上述风险度量假设P是已知的，但是在实际的应用中，P通常是从历史数据中估计或使用蒙特卡罗方法获得，有时也采用专家的判断，因此所得概率测度P不可避免地含有误差.为了控制模型风险，提出一致f－散度风险度量的稳健形式：

4 结 语

本文探索了如何给出一致风险度量中可接受集的可操作性表示，即把它转化为对f－散度的约束，通过上界c来表示概率测度间的距离，其中c的选取可参考CVaRα中的α.通过c的变化，所给出的一致f－散度风险度量能够表达决策者的风险厌恶，并且有多种表示方式.这一方法还可以直接用于组合优化和衍生产品的对冲问题，这类优化问题的求解留待以后详细探讨.

［1］ 任凤英，李兴斯.一致风险度量和锥优化分析［J］.运筹学学报，2010，14（2）：95－106.

REN Feng－ying，LI Xing－si.The cone optimization analysis of coherent risk measure［J］.Operations Research Transactions，2010，14（2）：95－106.（in Chinese）

［2］Follmer H，Knispel T.Entropic risk measures：coherence vs.convexity model ambiguity and robust large deviations［J］.Stochastics and Dynamics，2011，11（2－3）：333－351.

［3］Artzner P，Delbaen F，Eber J M，etal.Coherent measures of risk［J］.Mathematical Finance，1999，9（3）：203－228.

［4］Fllmer H，Schied A.Stochastic Finance—An Introduction in Discrete Time［M］.2nd ed.Berlin：Walter de Gruyter，2004.

［5］Fllmer H，Schied A.Convex measures of risk and trading constraints［J］.Finance and Stochastics，2002，6（4）：429－447.

［6］Frittelli M，Rosazza G E.Putting order in risk measures［J］.Journal of Banking ＆Finance，2002，26（7）：1473－1486.

［7］Ben－Tal A，Nemirovski A.Lectures on Modern Convex Optimization：Analysis Algorithms and Engineering Applications［M］.Philadelphia：SIAM，2001.

Coherent risk measure based onf－divergence

REN Feng－ying＊1，2， LI Xing－si1

（1.Institute of Operations Research and Control，Dalian University of Technology，Dalian 116024，China；2.College of Applied Mathematics，Beijing Normal University，Zhuhai，Zhuhai 519087，China）

The investigation for the coherent risk measures with entropy constraints is conducted，and because it has many good properties，the coherent risk measure withf－divergence constraints is presented.The study obtains a group of flexible risk measures and the methods to control the acceptable set of the coherent risk measure theory.In addition，its advantages used directly in optimization problems and the robustness of method are discussed.The new expression of coherent risk measure is obtained.It is the upper bound ofCVaRand more tractable in applications.

coherent risk measure；convex risk measure；coherent entropy risk measure；coherentfdivergence risk measure

O221.5

A

1000－8608（2013）05－0772－05

2012－03－16；

2013－07－01.

任凤英＊（1961－），女，博士生，副教授，E－mail：rui5926＠sina.com.