中国海外上市公司的PCA－SVM财务危机预警研究

黄 迅，张 颖，林 宇

（成都理工大学 商学院，成都 610059）

强化财务危机识别能力、提高财务危机预测精度、增强财务危机控制效果，不仅是广大上市公司时刻关注的重要问题，更是维护整个国家经济健康、稳定、持续发展的关键环节。尤其对我国海外上市公司而言，尽管它们与国内上市公司一样同为推动我国经济发展的重要力量，然而随着经济全球化的发展，我国海外上市公司面临着比国内上市公司更为复杂的经济环境［1］，来自财务危机的压力与挑战也就会大大超过国内上市公司。因此，建立科学有效的财务危机预警模型，对于我国海外上市公司成功地防范与化解财务危机，从而促进经济的稳定与繁荣具有重要意义。

长期以来，上市公司财务危机预警多以Z－Score多元判别分析（MDA）模型［2］、逻辑（Logit）回归模型［3，4］、概 率 比 （Probit）回 归 模 型［5］、KLR 信 号 模型［6］、主成分分析（PCA）模型［7］等传统的统计模型以及神经网络（Neural Networks）［8，9］等人工智能模型为主。虽然这些模型具有较强的泛化（Generalization）与容错性能，也取得了较好的研究效果并被实务界广泛应用［10］，但是这些模型却都存在前提条件过于苛刻、过学习（Over Fitting）、欠学习（Under Fitting）、局部极小（Local Minimization）等诸多问题［11］。为了弥补以上模型存在的缺陷，Vapnik提出了一种支持向量机（SVM）模型［12］。它是基于统计学习理论和结构风险最小化（Structural Risk Minimization，SRM）原则发展起来的一种新的机器学习与数据挖掘模型，能够有效地克服以上模型存在的过学习、欠学习以及局部极小等问题，具有自适应性等优越的学习能力与泛化推广能力［13，14］。基于此，本文运用SVM模型对我国海外上市公司财务危机预警进行研究。

但需要指出的是，SVM财务危机预警模型的预测能力是否优越，在很大程度上取决于选择的核函数（Kernel Function）［15］。但令人遗憾的是，目前还没有通用的核函数选择方法。不过，令人欣慰的是，已有学者利用最为常用的四种核函数，即线性（Linear）、多项式（Polynomial）、径向基（Radial Basis）和神经元的非线性作用（Sigmoid）核函数，分别构建SVM财务危机预警模型，并对其分类准确率进行比较，从而将基于使得分类准确率达到最高的核函数而建立起来的SVM模型确定为最终将要采用的预警模型［14，16］。鉴于此，本文也利用以上最为常用的四种核函数，分别建立我国海外上市公司的SVM财务危机预警模型并进行性能验证与评价，从中探索出一种具有最优学习能力与泛化推广能力的预警模型。

还需值得注意的是，海外上市公司财务数据往往呈现高相关性特征，从而容易引发数据冗余问题，导致SVM财务危机预警模型的预测精度大大降低［17］。而据周子 英等研 究成果［18］，PCA 方法能 够有效地解决财务数据之间因具有高相关性特征而造成的数据冗余问题。因此，本文在构建海外上市公司的SVM财务危机预警模型之前，还将引入PCA方法消除数据之间的高相关性特征，以提高模型的学习能力与泛化推广能力。

基于以上认识与分析，本文以我国海外上市公司为研究对象，运用PCA方法提取出对财务危机具有显著影响的特征指标，以此作为输入变量并运用SVM方法对我国海外上市公司财务危机预警进行研究，尤其重点探讨不同核函数对预警模型性能的影响，最终探索出一种具有最优学习能力与泛化推广能力的预警模型，并提出相应对策建议，为国家相关决策部门提供决策参考依据，为海外上市公司的管理层提供决策借鉴，为广大投资者合理投资提供科学指导。

一、海外上市公司的PCA－SVM财务危机预警模型的构建

（一）海外上市公司财务危机预警的SVM方法

支持向量机是由Vapnik最先提出的，其主要思想是建立一个分类超平面（the Separating Hyperplane）作为决策曲面，最大化正例与反例之间的隔离边缘。如图1所示，空心点和实心点分别代表两类样本，H为分类超平面，H1、H2分别代表过两类样本中离分类超平面H最近的样本且平行于H的超平面。它们到H的距离相等，并且这两个超平面之间的距离叫做分类间隔（margin）。所谓的最优分类面（the Optimal Separating Hyperplane）就是不但能将两类样本准确无误地分开（即训练错误率为0），而且能使分类间隔达到最大的超平面。

图1 最优分类面示意图

考虑到SVM的最大优势在于解决非线性不可分问题，本文将主要讨论该类问题。假设海外上市公司样本集为 （xi，yi），其中i＝1，2，…，n，表示海外上市公司数量为n。xi＝（xi1，xi2，…，xid）是d维特征指标向量，表示每家海外上市公司拥有d项财务比率指标。，其定义为：公司发生危机属于正类，用“＋1”表示，公司未发生危机属于负类，用“－1”表示。用数学模型为：

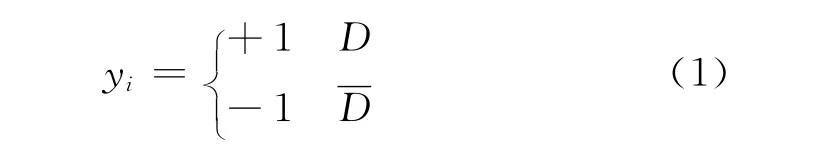
其中，D表示样本处于危机状态，D表示样本处于非危机状态。此时，在给定公司样本集（xi，yi）的前提条件下，构建SVM危机预警模型旨在寻找一个能够将发生危机和未发生危机的样本点正确分类的最优超平面。在的条件下，寻找最优分类面可以转化为求解如下最优问题：

其中，w是可调权值向量，b是偏置向量，ξi是非负的松弛变量（Slack Variable），其作用是适当地“软化”约束条件，允许样本错分情况的存在。换言之，允许样本错分就是允许将发生危机的公司误判为未发生危机的公司，或将未发生危机的公司误判

其中，α为引入的非负的拉格朗日乘子。根据Wolf对偶（Wolf Dual）定理，对L 关于w ，b，ξ求极大：

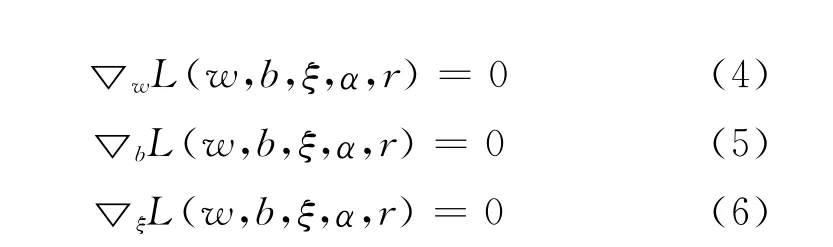
得到：

然后将上述式（7）、式（8）、式（9）中的极值条件代入式（3）中的拉格朗日函数中，并对α求极大，得到对偶（Dual）问题：

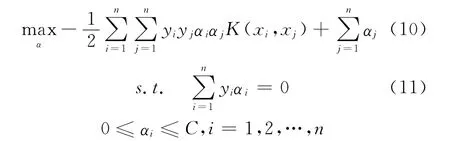
其中，K（xi，xj）是为了克服维数灾难（Curse of Dimensionality）而引入的核函数（Kernel Function），下文将会对核函数作具体介绍。

再将式（4）、式（5）、式（6）中的对偶问题转化为求极小，便得到最终的对偶问题：

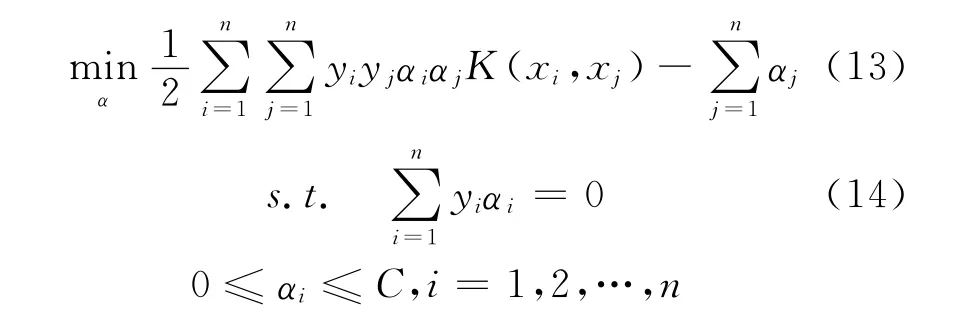
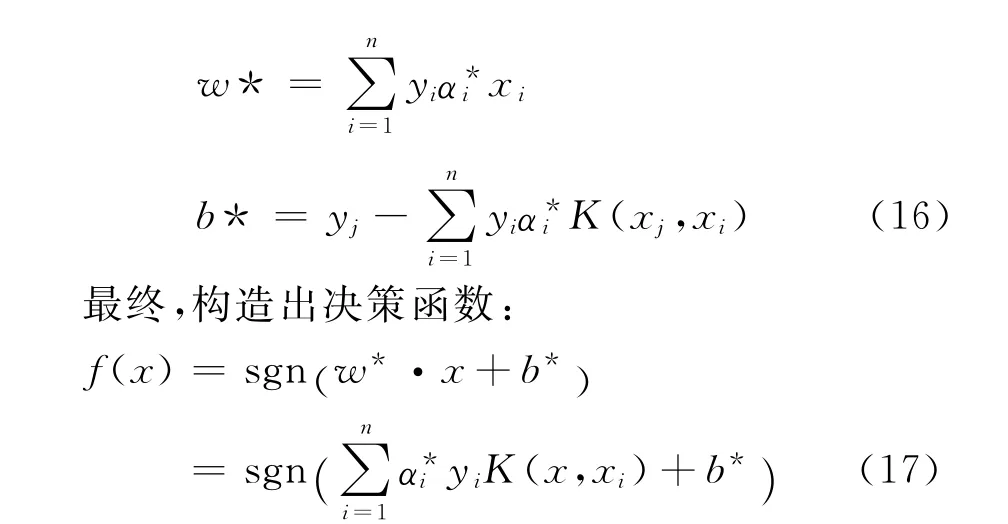
其中，sgn（ ）为符号函数，w＊为权向量，b＊为分类阈值（Threshold）。

基于上述SVM预警模型的构建可知，采用适当的内积（Inner Product）核函数 K（xi，xj）来替代原空间中的内积 （xi，xj），既可以实现非线性变换后的线性分类，又避免了维数灾难的发生。维数灾难之所以产生，是因为低维空间线性不可分的模式尽管通过非线性映射到高维特征空间后实现了线性分类，却同时也造成了维数越高、计算量越大的问题，而借助核函数技术就能够有效地解决“维数灾难”问题［19］。核函数的形式有多种，采用不同的核函数将产生不同的支持向量机，形成不同的分类预警方法。常见的核函数有：

（二）基于PCA的财务危机特征指标提取

尽管上文通过SVM方法构建出了海外上市公司财务危机预警模型，然而，海外上市公司财务数据往往呈现高相关性特征，从而容易引发数据冗余问题，导致SVM财务危机预警模型的预测精度大大降低，而PCA方法正好能够有效地解决财务数据之间因具有高相关性特征而造成的数据冗余问题［18］。因此，本文在构建海外上市公司的SVM财务危机预警模型之前，还将引入PCA方法消除数据之间的高相关性特征，从而提升模型的学习能力与泛化推广能力。

在本文中，对于每一个具有d维特征指标的公司而言，其特征指标为xj，j＝1，2，…，d，表示公司的第j项特征指标。于是，对公司的特征指标便展开如下的PCA分析：

（1）计算方差－协方差矩阵：

其中

在式（19）中，xti和xtj分别表示第t家公司的第i项和第j项特征指标；Ε（xi）和Ε（xj）分别表示第i项和第j项特征指标的均值，i、j＝1，2，…，d。

其中，设λ1≥λ2≥…≥λd，称F1为第1个主成分，同理，Fd为第d个主成分。

（4）若取前p（p≤d）个主成分，则F1、F2、…，Fp的累计贡献率为：

其中，第一主成分F1的贡献率最大，这表明F1综合公司特征指标x1、x2、…、xd的能力最强，依此类推，Fp的贡献率最小，这表明Fp综合公司特征指标x1、x2、…、xd的能力最弱。

（5）经过PCA得到的新样本集为 （Fi，yi），其中，Fi＝ （Fi1，Fi2，…，Fip），i＝1，2，…，n。

至此，基于PCA的特征指标提取已完成。于是，将提取出对财务危机具有显著影响的p个主成分因子作为输入指标，就能够运用SVM方法建立海外上市公司财务危机预警模型。

（三）特征指标的归一化处理

对每家海外上市公司而言，其特征指标之间的数量等级可能相差很大，这将会导致较大值的输入

式中，xmean为原样本中第k列数值的均值，xvar为原样本中第k列数值的方差。

（四）实验设计

根据PCA－SVM基本原理的概述，下文将就如何构建海外上市公司财务危机预警模型进行实验设计。

1．样本及其对应的财务预警指标的选取

本文的样本是从截止到2010年末在美国的Nasdaq及纽约证券交易所上市的中国公司中随机选择的n家公司。本文之所以将我国海外上市公司样本定位在美国的Nasdaq及纽约证券交易所中选取，是因为我国海外上市公司中的绝大部分是在美国的Nasdaq及纽约证券交易所上市，从这两大证券市场中选择出来的样本在我国众多海外上市公司中最具代表性。然后，再从这n家海外上市公司2009年12月的财务报表数据中提取出d项财务比率指标作为样本指标。由于公司的盈亏状况直接决定着公司是否会发生财务危机，而净利润的正负恰好能够直接反映公司的盈亏状况。因此，本文以净利润的正负作为评判公司财务是否发生危机的标准。在此基础上，这n家公司被划分为财务正常类公司（用“－1”来表示）以及财务危机类公司（用“＋1”来表示）。由此，构成样本集 （xi，yi），i＝1，2，…，n，输入数据xi＝ （xi1，xi2，．．．，xid）是d维特征指标覆盖较小值的输入指标，从而可能影响PCASVM模型的预测精度。为了减少预测误差，本文在构建模型前，将采用归一化（Normalization）数据预处理方法，将公司的特征指标值映射（Map）到区间［0，1］之间。数据归一化的常用方法有多种，其中平均数方差法是进行PCA分析之前惯用的一种归一化方法。因此，本文采用平均数方差法对原样本集（xi，yi）的输入变量特征指标进行归一化，得到新的公司样本集

2．特征指标的归一化预处理

为了避免因特征指标之间的数量级差别而造成模型的预测精度下降，本文在构建PCA－SVM预警模型前，将采用平均数方差法的归一化数据预处理方法，将样 本集 （xi，yi）的输 入特征 指标映射（Map）到区间 ［0，1］之间，由此获得新的数据样本集 （，yi）。

3．基于PCA的财务危机特征指标提取

由于在特征指标的归一化预处理中仅仅消除了这d项特征指标之间的数量级差别，而并未解决各指标之间存在的高相关性问题，因此本文采用PCA方法提取出p个相互独立的主成分，在减少样本数据维数的同时也消除各指标之间线性相关的冗余成分，从而提高SVM财务危机预警模型的学习能力与泛化推广能力。

4．训练集与测试集的划分

为了保证实验设计的公平性与准确性，我们将样本及指标选取中的n个样本随机地平均划分为训练集与测试集，每类集合中都分别包含着一部分财务正常类公司与财务危机类公司。

5．参数选取

考虑到参数的选取是一个复杂的过程，并且参数值的大小会直接影响模型的训练与预测效果，因此为了选择出能够保证训练与预测效果达到最优的参数，本文运用最为常用的k交叉验证法（K－fold Cross Validation，K－CV）来选择最佳的惩罚参数c和核函数参数g。所谓k交叉验证，即将原始数据均分为k组，将每组子集数据分别当作一次验证集，与此同时，其余的k－1组子集数据当作训练集，于是得到k个模型，将这k个模型最终验证集的分类准确率的平均值作为此K－CV下分类器的性能指标。采用k交叉验证法，能够有效地避免产生过学习与欠学习问题，从而优化模型的训练效果，提升模型的泛化推广能力［20］。

6．不同核函数下模型的训练

为了深入探讨不同核函数对预警模型性能的影响，本文以参数选取中选取出来的最佳参数为基础，利用训练集在不同的核函数下对模型进行训练，从而获得不同的SVM预警模型。

7．模型可靠性检验

为了评价模型的泛化推广能力，我们利用测试集对SVM预警模型进行性能验证，从中选择出拥有最高分类准确率的模型作为我国海外上市公司的财务危机预警模型。

二、实证结果与分析

（一）样本选择及原始数据处理

本文以我国海外上市公司2010年的净利润为标准，从在美国Nasdaq以及纽约证券交易所上市的中国公司中选择了57家财务正常公司，其中30家被划入训练集合，剩余27家被划入测试集合，并用“－1”表示它们所属财务正常类。另外选择了23家财务危机公司，其中10家被划入训练集合，剩余13家被划入测试集合，并用“＋1”表示它们所属财务危机类。

在此基础上，本文通过借鉴以往研究文献并参考公司业绩评价指标体系，从以上80家海外上市公司2009年12月的财务报表数据中选取出能够综合反映公司的短期偿债能力、长期偿债能力、营运能力和盈利能力四方面的15项财务比率指标作为样本指标。（样本指标见表1）

表1 财务比率指标

需要说明的是，之所以样本指标的选择年度定位在判定公司是否发生财务危机的上一年（即公司2010年被判定为财务正常类或财务危机类，则选用2009年的财务数据），是因为这样能够提前一年预测海外上市公司是否会出现财务危机，从而避免对模型预测能力的高估。本文主要使用Matlab2011b软件分析数据。

本文首先对各项财务比率指标数据进行归一化处理，得到新的财务比率指标数据x＊i，i＝1，2，…，15，并运用PCA方法提取出6个主成分因子，其累积贡献率达到79．658%，从而说明，提取出的这6个主成分因子能够比较全面地反映我国海外上市公司的财务状况。

（二）不同核函数下预警模型的可靠性检验

将以上6个主成分因子作为输入指标，就能运用SVM方法建立海外上市公司财务危机预警模型。

首先，在划分出训练集与测试集的基础上，本文运用k交叉验证法选择最佳的惩罚参数c和核函数参数g。实验结果显示，最佳惩罚参数c为1．0718，最佳核函数参数g为0．35355。

由于训练SVM模型除需要选择参数c、g外，还需要选择合适的核函数类型。因此，在获得最佳参数c和g的基础上，本文利用训练集对不同核函数下的SVM进行训练，从而寻找到最佳的核函数类型（结果见表2）。

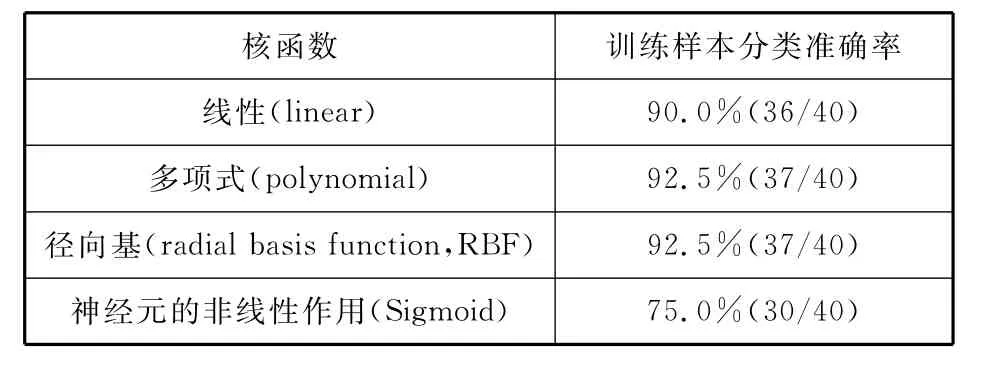
表2 不同核函数下的训练样本分类准确率

从表2可见，采用多项式核函数和径向基核函数的训练样本分类准确率最高，说明基于这两类核函数的SVM模型具有最为优越的学习能力。

此外，通过展示图2～图5，能够更加直观地看到在不同核函数下训练样本的具体分类情况。其中，“○”代表实际训练集分类；“×”代表预测训练集分类；横坐标表示训练集样本，图2～图5中显示出本文训练集样本数共40个；纵坐标表示样本的类别标签，即“＋1”和“－1”两类。此外，从图2～图5可以观察到，当预测训练集分类与实际训练集分类一致，即模型对于训练样本是否发生危机的实际与预测情况判断正确时，“○”与“×”便重合在一起，否则就相分离（见图2～图5）。

从图2可以看到，在训练样本集的前30个财务正常类公司中出现1个“○”与“×”相分离的情况，即表示出现1个被错划为财务危机类公司的情况；后10个财务危机类公司中出现3个“○”与“×”相分离的情况，即表示出现3个被错划为财务正常类公司的情况。从图3中可以看到，在训练样本集的前30个财务正常类公司中未出现被错划为财务危机类公司的情况；后10个财务危机类公司中出现3个被错划为财务正常类公司的情况。从图4中可以看到，在训练样本集的前30个财务正常类公司中未出现被错划为财务危机类公司的情况；后10个财务危机类公司中出现3个被错划为财务正常类公司的情况。从图5中可以看到，在训练样本集的前30个财务正常类公司中出现4个被错划为财务危机类公司的情况；后10个财务危机类公司中出现6个被错划为财务正常类公司的情况。

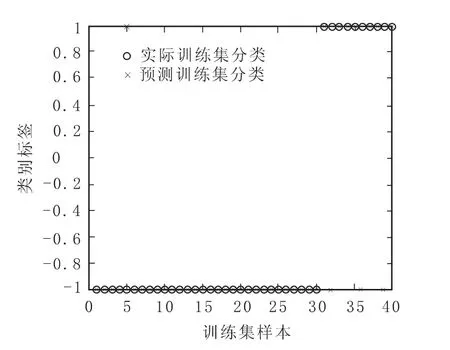
图2 线性核函数下训练样本集分类图

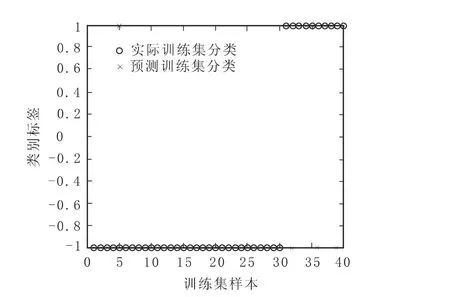
图3 多项式核函数下训练样本集分类图

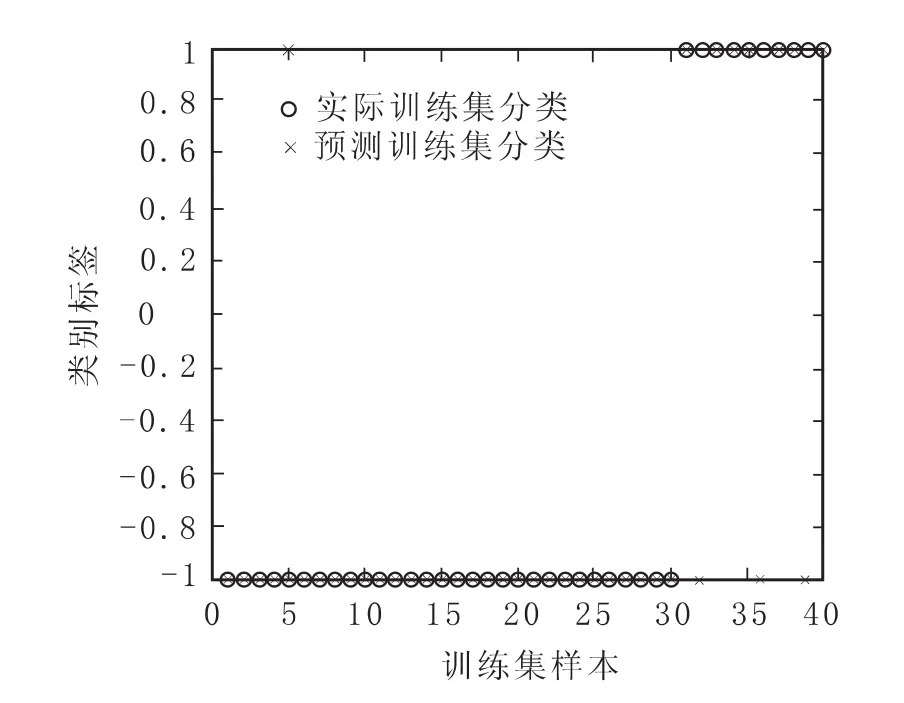
图4 径向基核函数下训练样本集分类图

虽然在多项式核函数和径向基核函数下训练出的SVM模型具有最为优越的学习能力，但其泛化

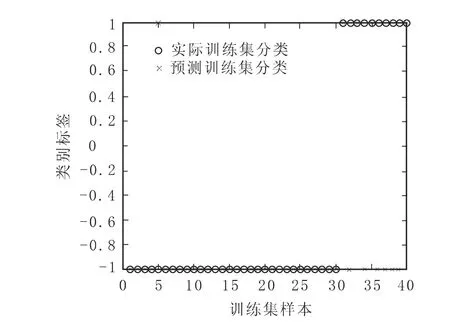
图5 sigmoid核函数下训练样本集分类图

推广性能是否优越还不可知。因此，我们还需要通过测试集对训练出的模型进行性能验证与评价，从而寻找到泛化推广性能最为优越的SVM模型（结果见表3）。

表3 不同核函数形式下的测试样本分类准确率

从表3可以看到，采用径向基核函数和神经元的非线性作用核函数的测试样本分类准确率最高，说明基于这两类核函数训练出的SVM模型具有最为优越的泛化推广性能。

此外，通过展示图6～图9，能够更加直观地观察到在不同核函数下测试样本的具体分类情况（见图6～图9）。

从图6中可以看到，在测试样本集的前27个财务正常类公司中出现1个被错划为财务危机类公司的情况，后13个财务危机类公司中出现8个被错划为财务正常类公司的情况。从图7中可以看到，在测试样本集的前27个财务正常类公司中出现2个被错划为财务危机类公司的情况，后13个财务危机类公司中出现7个被错划为财务正常类公司的情况。从图8中可以看到，在测试样本集的前27个财务正常类公司中未出现被错划为财务危机类公司的情况，后13个财务危机类公司中出现8个被错划为财务正常类公司的情况。从图9中可以看到，在测试样本集的前27个财务正常类公司中出现1个被错划为财务危机类公司的情况，后13个财务危机类公司中出现8个被错划为财务正常类公司的情况。

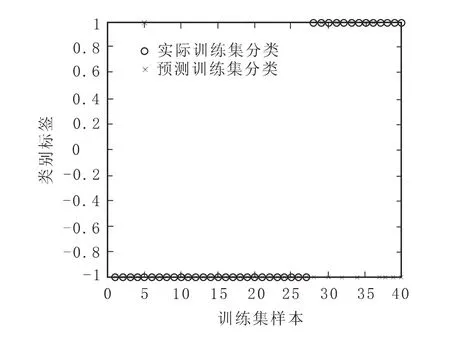
图6 线性核函数下测试样本集分类图

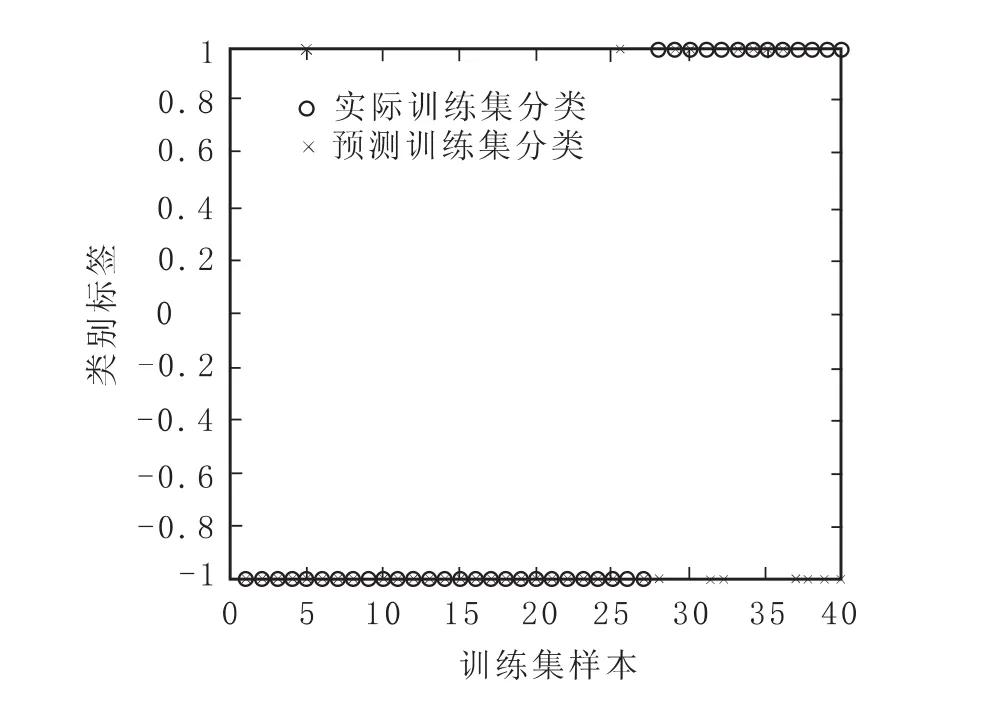
图7 多项式核函数下测试样本集分类图

图8 径向基核函数下测试样本集分类图

图9 sigmoid核函数下测试样本集分类图

因此，对比表2与表3可见，在表2中，在线性核函数下训练样本分类准确率为90%，即40个训练样本分类中出现4个被错分的样本；在多项式核函数下训练样本分类准确率为92．5%，即40个训练样本分类中出现3个被错分的样本；在径向基核函数下训练样本分类准确率为92．5%，即40个训练样本分类中出现3个被错分的样本；在神经元的非线性作用核函数下训练样本分类准确率为75%，即40个训练样本分类中出现10个被错分的样本。从中分析可知，在多项式核函数与径向基核函数下训练得到的预警模型所达到的分类准确率是最高的。另外，表3中，在线性核函数下测试样本分类准确率为77．5%，即40个测试样本分类中出现9个被错分的样本；在多项式核函数下训练样本分类准确率为77．5%，即40个测试样本分类中出现9个被错分的样本；在径向基核函数下训练样本分类准确率为80%，即40个测试样本分类中出现8个被错分的样本；在神经元的非线性作用核函数下训练样本分类准确率为75%，即40个测试样本分类中出现8个被错分的样本。从中分析可知，在径向基核函数与神经元的非线性作用核函数下测试样本分类准确率是最高的。

综上所述，PCA－SVM财务危机预警模型在线性、多项式、径向基和sigmoid四种核函数下都具有良好的预测能力，而径向基核函数下的PCA－SVM财务危机预警模型较其他主要核函数下的模型而言，具有更加优越的学习能力与泛化推广能力。

三、结论

本文以我国海外上市公司为研究对象，运用PCA方法提取出对财务危机具有显著影响的特征指标，利用训练集在不同核函数下对SVM进行训练，运用测试集对训练出的SVM财务危机预警模型进行性能验证与评价，从中寻找出一种具有最优学习能力与泛化推广能力的SVM财务危机预警模型。实证研究结果表明，PCA－SVM财务危机预警模型在线性、多项式、径向基和sigmoid四种核函数下都具有良好的预测能力，而径向基核函数下的PCA－SVM财务危机预警模型具有更加优越的学习能力与泛化推广能力。

基于以上实证结果，本文认为，基于径向基核函数的PCA－SVM财务危机预警模型能够有效地预测我国海外上市公司是否会发生财务危机，从而能够为我国相关决策部门、海外上市公司管理层以及广大投资者提供宝贵的决策参考。

最后需要指出的是，尽管本文仅仅运用四种核函数下的PCA－SVM方法对我国海外上市公司财务危机预警进行实证研究，然而，本文的研究技术、方法与相关结论对于我国海外上市公司进行财务危机预警仍然具有一定的借鉴意义。

［1］张艳慧，周雪峰．中国公司海外上市优劣势分析［J］．中小企业管理与科技（下旬刊），2010，（9）：76－77．

［2］Altman．Financial Ratios，Discriminant Analysis and the Prediction of Corporate Bankruptcy［J］．Journal of Finance，1968，23（4）：589－609．

［3］Ohlson．Financial Rations and the Probabilistic Prediction of Bankruptcy［J］．Journal of Accounting Research，1980，18（1）：109－130．

［4］Laitinen E K．Predicting a corporate credit analyst’s risk estimate by logistic and linear models［J］．International Review of Financial Analysis，1999，8（2）：97－121．

［5］Zmijewski．Methodological issues related to the estimated of financial distress prediction models［J］．Journal of Accounting Research，1984，22（1）：59－82．

［6］Kaminsky，C．，Lizondo，S．and Reinhart，C．Leading Indicatiors of Currency Crises［R］．MF staff paper，1998，45（1）：1－48．

［7］张爱民，祝春山，许丹健．上市公司财务失败的主成分预测模型及其实证研究［J］．金融研究，2001，（1）：10－25．

［8］Odom，Sharda．Neural Network for Bankruptcy Prediction［C］．International Joint Conference on Neural Network，1990：17－70．

［9］Desai V S，Crook J N，Overstreet G A．A comparison of neural network and linear scoring models in the credit union environment［J］．European Journal of Operational Research，1996，95（1）：24－37．

［10］王小黎．SVM模型在河南省中小企业技术创新能力评价中的应用［J］．科技管理研究，2011，（9）：92－95．

［11］陈守东，杨莹，马辉．中国金融风险预警研究［J］．数量经济技术经济研究，2006，23（7）：36－48．

［12］Vapnik V N．The Nature of Statistical Learning Theory［M］．1995．

［13］邓乃扬，田英杰．数据挖掘中的新方法－支持向量机［M］．第三版．北京：科学出版社，2006．

［14］杨海军，太雷．基于模糊支持向量机的上市公司财务困境预测［J］．管理科学学报，2009，12（3）：102－110．

［15］Aronszajin N．Theory of reproducing kernels［J］．Transactions of the American Mathematical Society，1950（68）：337－404．

［16］宋新平，丁永生．基于最优支持向量机模型的经营失败预警研究［J］．管理科学，2008，21（1）：115－121．

［17］刘雷．应用EN、PCA和RBF网络评价建设项目动态联盟的候选投标项目［J］．管理评论，2010，22（2）：121－128．

［18］周子英，段建南，向昌盛，陈茜．基于PCA－SVM的区域经济预测研究［J］．计算机仿真，2011，28（4）：375－378．

［19］Aizerman M．A，Braverman E．M，Bozonoer L．I．Theoretical foundations of the potential function method in pattern recognition learning．Journal of Machine Learning Research，2000．http：／／www．jmlr．org．113－114．

［20］郭文伟．基于支持向量机的股市风格轮换策略研究［J］．管理科学，2009，22（6）：101－110．