基于CDM机制的国际碳排放权贸易价格波动性研究

黄晓凤，程玉仙，唐嘉徽

（1.广东商学院 国民经济研究中心，广东 广州 510320； 2.中南林业科技大学 经济学院，湖南 长沙 410004）＊

一、引言

随着全球气候变化问题日益突出，发展碳排放权新型国际贸易日益成为国内外理论界关注的焦点之一。随着其他减排措施实施成本的增加和全球低碳经济的蓬勃发展，碳排放权的国际贸易已不容回避。而碳排放权国际贸易的核心问题是碳排放权价格问题，只要寻找到通过公平、公正、公开的交易程序产生的价格，并在正常的范围内波动，碳排放权国际贸易中的一切问题都将不再是问题。如贸易价格异常波动，不是互利的贸易无法发生，就是造成减排成本提高、社会资源浪费和新能源技术开发受阻。因此，研究价格波动规律，制定科学的定价机制，使价格尽可能地接近边际减排成本，既达到公平贸易、创造收入的目的，也达到实现全球减排资源最优配置和全球温室气体减排目标，非常必要。

从现有文献看，学者们对国际碳排放权的贸易价格问题进行了一些研究，但比较零散，且主要集中在欧盟排放贸易体系（EU ETS）价格决定以及石油价格波动对碳市场的溢出效应等方面。例如，张云、杨来科（2011）指出对于国际碳排放权贸易而言，市场均衡时各个国家的边际减排成本等于排放权价格［1］。Emilie Alberola和Julien Chevallier（2008）等发现碳排放权价格不仅反映能源价格、天气变动，而且和宏观经济活动有关［2］。王俊丽（2012）等认为国际石油价格波动对国际碳市场贸易价格具有波动溢出 效 应［3］。Sonia Labatt and Rodney R.White（2007）提出需进一步提高碳价格透明度，才能有效发挥价格引导机制［4］。洪涓（2010）等发现EU ETS市场引导CDM机制下碳排放权核证减排单位（简称CERs）市场，二者具有趋同趋势［5］，黄明皓（2010）等研究结果显示：EU ETS市场和CERs市场的现货价格和期货价格存在双向波动效应［6］。

这些研究对国际碳排放贸易的发展和全球减排目标的实现都有重要理论意义和实践价值。但不足之处在于：第一，国际碳排放权市场贸易形式与贸易产品呈现多样化趋势，在过分抽象前提下讨论买卖双方的定价行为，忽视了碳排放交易价格决定的复杂性；第二，学者的研究大多从理论层面研究国际碳排放权贸易价格的决定原理，通过碳排放贸易市场真实数据进行实证研究直接探究价格波动规律的不多；第三，研究欧盟排放贸易市场价格影响因素相对较多，而对于清洁发展机制（CDM）下国际碳排放市场的价格影响因素及波动规律的研究尚不多见。在国际碳排放权贸易市场上，中国是CDM项目的最大供应国，因此，本文拟选择CDM机制下CERs市场价格为研究对象，从宏微观层面对国际碳排放权贸易价格波动的影响因素进行研究，并希望通过理论和实证研究寻求市场价格波动规律，丰富碳排放权国际贸易价格理论，同时为中国参与国际碳排放权贸易取得定价权提供应对之策。

二、研究CERs价格波动的理论模型

Engle（1982）首次提出的ARCH模型［7］和Bollerslev（1986）扩展的GARCH模型［8］能准确捕捉到资产随机波动性特征，对时间序列变化中存在的异方差和波动率聚类现象进行了很好的描述，因此，本文运用GARCH模型对国际碳排放权市场波动规律进行研究。

ARCH模型的主要思想是随机误差项μt的条件方差依赖于它的前期值μt－1的大小。设yt为因变量，xt为自变量，在t时刻可获得的信息集为Ωt－1的假定条件下，随机误差项μt以0为期望值，σ2t为条件方差的正态分布。ARCH（q）的均值方程和方差方程分别为：

其中，常数ω＞0，参数αi≥0（i＝1，2，…，q），γ是待估参数。ARCH（q）模型表明随机误差项μt是服从q阶的ARCH过程，市场当期或未来的波动受市场过去波动的正向影响。

ARCH（q）模型刻画了市场波动的持续性特征，但不能反映实际数据的长期记忆性和非线性等问题，对此，Bollerslev（1986）提出了广义自回归异方差（GARCH）模型，即在ARCH（q）模型的方差方程中加入条件方差的滞后项，于是将方程式（2）拓展为式（3）：

式中，p为自回归项（GARCH项）滞后阶数、q为残差平方项（ARCH项）的滞后阶数，p≥0，q≥0；αi≥0（i＝1，2，…q），βj≥0（j＝1，2，…p），αi、βj为参数。

式（3）被称为序列服从GARCH（p，q）过程，GARCH（p，q）过程是平稳过程的充分必要条件是：

式（3）表明，t时刻下的随机误差项μt的条件方差依赖于t－i时刻下的残差（ARCH项）的大小和方差的预测值（GARCH项）。即为过去所有残差的正加权平均，这正与波动聚类现象相吻合：随机误差项在大幅度波动后趋向于有更大的波动，小幅度波动后趋向于有更小的变化。因此，GARCH模型对时间序列变化中的波动聚类现象有很好的解释力，从而提高了对价格波动规律研究的精准度。

GARCH模型对于国际碳排放权贸易价格波动规律研究具有重要实际意义。GARCH模型易于发现时间序列变化中存在的异方差和波动聚类性，而国际碳排放权交易市场的历史CERs价格变化就是一典型具有异方差性和聚类性的序列，所以很适合用GARCH模型对CERs价格变化规律和趋势进行分析。根据模型，残差反应了因变量CERs价格的实际值偏离均值方程拟合值的大小，因此，可以通过不变方差ω、t－j时刻方差的预测值（GARCH项）及t－i时刻下的残差（ARCH项）的加权平均来预测CERs当期或未来的价格。

三、CERs价格波动的实证分析

（一）数据的选取和预处理

结合数据的可获得性、连续性及典型性要求，本文以欧洲气候交易所交易品种为CERs（单位为欧元/吨二氧化碳当量）现货的日交易收盘价数据作为研究样本。时间序列为2008年3月14日～2011年12月9日。样本数据来自Wind数据库，运用Eviews6.0进行操作。以往大量研究表明，GARCH模型能够较好地刻画收益率波动聚类现象，因此，本文从收益率的视角，研究CERs价格的波动规律，并将收益率指标rt定义为：

式（5）中，pt为t期的收盘价，pt－1为t－1期的收盘价，根据式（5）运用Eviews6.0计算出收益率数据，并得日收益率的描述性统计特征（见图1）。

由图1可知：收益率序列的均值是－0.120295，接近0，符合收益率指标的普遍特征；偏度为－0.240003，说明收益率序列分布略微左偏；峰度为5.806550，明显高于正态分布的峰值3；而JB＝317.1914，且其相伴概率为0，显著拒绝正态分布的假设。因此，可以得出结论：CERs收益率序列与大多数金融时间序列一样，呈现出“尖峰厚尾、不对称分布”的特征，初步具备建立GARCH（p，q）模型的条件。

（二）单位根检验

由于GARCH（p，q）模型只适用于平稳序列建模，因此，首先对CERs收益率序列进行单位根检验（ADF），检验结果见表1。

图1 CERs日收益率统计分布

表1 CERs收益率序列的ADF检验

从表1可知，CERs收益率序列的ADF检验统计量为－29.06323，小于不同显著水平下的临界值，且相伴概率P值为0，说明CERs收益率序列均在1%的显著性水平下拒绝存在单位根的原假设，由此得到CERs收益率序列是平稳的，无需差分就可以直接建立模型。

（三）模型的建立与波动规律分析

1.ARCH模型与波动聚集性检验。通过CERs收益率的自相关函数和偏相关函数图（在此图略），发现CERs收益率的滞后4阶的相关性比较显著，因此，其均值方程为：

OLS回归结果为：

方程的拟合效果并不是很好，从残差图（图略）可以看出，CERs收益率序列并没有呈现出规律性波动，而是表现出很强的时变性、突发性和波动聚集性特征，即模型可能存在异方差，因此，需对模型进行ARCH效应检验。对回归方程的残差进行滞后1～4期的ARCH－LM检验，其检验结果是F－statistic和Obs＊R－squared的相伴概率P值均为0.0000，拒绝“残差不存在ARCH效应”的原假设，因此，可以建立GARCH模型。

2.GARCH模型及波动持续性检验。根据ARCH检验，在此建立GARCH（1，1）模型，均值方程为式（6），条件方差方程为：

对其参数进行估计的结果见表2。

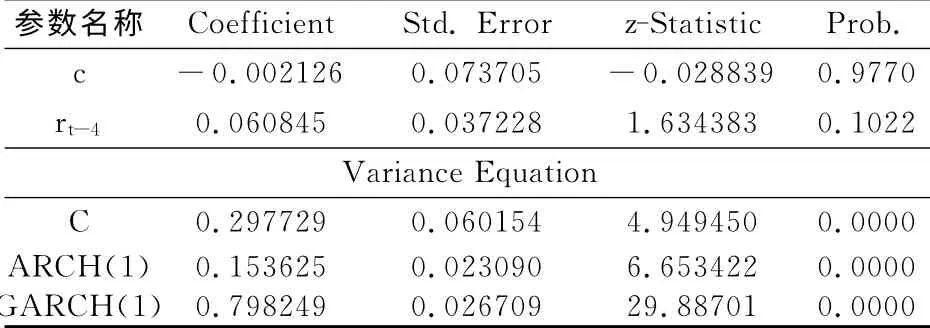
表2 GARCH（1，1）回归结果

根据估计结果，均值方程和方差方程分别表示为：

再对模型进行ARCH－LM检验，发现F统计量为0.2863，相伴概率为0.5927，接受“残差不存在ARCH效应”的原假设，说明GARCH（1，1）模型很好地消除了残差序列的条件异方差性，因此，均值方程和方差方程还是比较合理的，模型具有一定的解释力。

由表2可知，参数估计系数都是统计显著的，表明GARCH（1，1）模型能够很好的拟合数据，方差方程中的ARCH项系数α为0.153625大于0，说明外部冲击会加剧CERs价格的波动，同时GARCH项系数β为0.798249小于1，表明CERs价格的波动具有一定的持续性。α＋β＝0.9519＜1，满足GARCH（1，1）模型中参数的约束条件。由于方差方程中系数之和又非常接近1，说明外部冲击引起CERs价格的波动时间会比较长，持久性特征明显。因此，模型对未来价格的预测和波动规律的掌握具有重要作用。

3.非对称效应的检验。在国际碳排放权CERs市场运行过程中，是否存在CERs价格波动的非对称性呢？在此，运用TGARCH（1，1）模型检验，均值方程为（6）式，条件方差方程为：

回归结果见表3。

表3 TARCH（1，1）模型回归结果

根据估计结果，均值方程和方差方程分别表示为：

在TARCH（1，1）模型中，杠杆效应项的系数φ＝0.116975，说明CERs价格的波动具有“杠杆效应”：利空负面冲击能比等量的利好正面冲击产生更大的波动。当国际宏观经济形势趋好、或股票和汇率等市场价格上升、或CERs签发率增加等利好消息出现时，μt－1＞0，则Dt－1＝0，利好消息只会对CERs价格带来0.090589（α的估计值）倍的冲击；当国际有关气候变化政策不明朗，或发生全球金融危机等利空消息出现时，μt－1＜0，这时，Dt－1＝1，利空消息会带来0.207564（α＋φ估计值）倍的冲击。

利空冲击比等量利好冲击对CERs价格产生更大波动的结果在EGARCH模型中也能得到印证，在EGARCH模型（检验过程在此略）中，α的估计值为0.294304，非对称项φ的估计值为－0.068714。当μt－1＞0，利好信息对CERs价格序列条件方差的对数带来0.294304－0.068724＝0.22558倍的冲击，当μt－1＜0，利空信息对CERs价格序列条件方差的对数带来0.294304＋（－0.068714）×（－1）＝0.363018倍的冲击。

四、结论与建议

以上运用基于GARCH模型族的实证分析，探讨了国际碳排放权CERs市场的价格波动，研究结果表明：（1）CERs市场价格波动是政治博弈、国际宏观经济形势和气候变化等多重因素共同冲击的结果。共赢性博弈均衡、全球经济繁荣、气候变化趋暖、国际原油和股票等市场价格上涨及CERs签发率增加等对CERs市场价格波动构成利好信息冲击；反之，零和博弈或负和博弈、国际经济危机及CERs签发率减少等对CERs市场价格波动构成利空信息冲击。（2）CERs市场价格波动具有很强的波动聚类性与持续性。CERs市场价格并非规律性波动，而是有很强的时变性和波动聚集性特点。GARCH模型检验得出α＋β＝0.9519非常接近1，说明在美国经济复苏缓慢、欧洲深陷债务危机等利空信息冲击下，波动会持续下去。（3）CERs价格波动存在杠杆效应。TARCH模型表明，CERs价格“杠杆效应”明显，主要是国际金融危机和欧债危机等多重利空相互叠加带来持续的悲观预期，因此，每一次利空信息都比利好信息导致CERs价格更大的波动。

目前，我国已成为全球CERs市场最大供给方，作为CDM项目卖方参与CERs一级市场交易就成为我国参与国际碳排放权贸易的唯一途径，在碳排放权市场，一级市场以二级市场的现货价格为定价基础。因此，我国在参与CERs一级市场贸易时，为了与国际碳贸易市场价格保持同比例上升、达到高价出售的目的，首先积极参与国际气候环境条款的谈判，制定互利共赢的新规则，对市场价格形成持续利好信息冲击；其次必须掌握CERs二级市场价格波动的聚类性、持续性和杠杆性特征，分析CERs二级市场价格波动趋势；再次，根据波动规律选择恰当的贸易时机，尽可能地在CERs二级市场价格接近上升通道顶端时或下降通道起点时出售；最后，建立CDM项目投资风险管理体系，避免利空信息冲击的杠杆效应。

［1］张云，杨来科.国际碳排放权交易价格决定与最优出口规模研究［J］.财贸经济，2011，（7）：70－78.

［2］Alberola E.，Chevalier J.，Cheze B.Price drivers and structural breaks in european carbon prices 2005－2007［J］.Energy Policy，2008（39）：787－797.

［3］王俊丽.国际石油价格波动对碳市场溢出效应研究［J］.经济研究导刊，2012，（5）：70－72.

［4］Sonia Labatt and Rodney R.White.Carbon Finance：The financial implications of climate change［M］.John Wiley ＆Sons，Inc，2007.

［5］洪涓，陈静.国际碳排放权交易价格关系实证研究［J］.中国物价，2010，（1）：7－11.

［6］黄明皓，李永宁，肖翔.国际碳排放交易市场的有效性研究——基于CER期货市场的价格发现和联动效应分析［J］.财贸经济，2010，（11）：131－137.

［7］乔榛，魏枫.世界性碳减排合作的出路［J］.税务与经济，2011，（5）：1－5.

［8］Engle，Robert.F，Autoregressive conditional heteroskedasticity with estimates of the variance of U.K.inflation［J］.Econometrica，1982，（50）：987－1008.

［9］吴硕，何菊莲.低碳经济研究的主要内容和方法——近10年国内外研究文献比较［J］.湖湘论坛，2011，（5）：94－98.

［10］黄晓凤，鲁志坚.贸易保护主义的新变化对中国出口企业的影响及应对［J］.湖南大学学报（社会科学版），2010，（6）：67－71.

［12］Bollerslev T.，Generalized autoregressive conditional heteroskedasticity［J］.Journal of Economics，1986，（31）：307－327.