6-DOF仿生机器马模型分析与运动控制

哈斯花，赵静波

（1,赤峰工业职业技术学院，内蒙古 赤峰 024000；2.首钢迁安钢铁有限责任公司冷轧作业部，河北省迁安 064400）

仿生机器人是仿生学的各种先进技术与机器人领域的各种应用目的的结合，是模拟自然界中生物的运动机理、行为方式等的机器人系统.目前，基于并联机构的仿生型机器人已经应用于军事侦察、航空航天、疾病检查等领域.

通过运动机理进行位移运动仿生的机器马系统，通过模拟马的各种运动，结合实时检测的人体脉搏、血压、呼吸等各项检测指标，建立人体运动数据库，可达到医疗疾病检测、运动健身的目的.而机器人的动力学建模是机器马驱动系统和控制系统设计的基础，也是机构动力学性能评价、动力学优化设计及实时控制的必要条件.

1 结构设计

文献[1]中，作者基于Stewart平台变异得到了一种新型六自由度正交并联机构，即3－2－1－PSS三维平台并联机构，它由动平台、六条运动支链和基座构成，其布局为每一个运动支链构成一个分支，支链由两个球铰、连杆和直线移动副组成，并通过球铰与动平台相连.六个分支按3、2、1分为第一、第二、第三组，分别于动平台的3个相互垂直的平面相连.第一组支链的球铰中心（C1，C2，C3）分布在以平面中心为中心的等腰三角形的三个顶点上，第2组支链的球铰中心（C4，C5）分布在过平面中心、以平面上下两边平行的线段端点上，第3组支链的球铰中心（C6）位于平面的中心，平台结构如图所示.基于运动机理进行位移运动仿生的机器马系统采用该正交并联机构作为仿生运动平台，马模型的重心位于动平台的中心，通过驱动六个轴系同步协调运动来完成马的各种运动状态.为了计算方便，涉及仿生运动平台质心时，假定所有质量都位于平台的中心点.

2 仿生机器马模型分析

2.1 运动学分析

为了研究仿生机器马的运动、建模与控制，建立与运动平台固接的坐标系：{P}：O'-x'y'z'，原点O'位于运动平台的上平面中心，三个坐标轴分别与运动平台的三个相互垂直的边平行；建立与基座固接的坐标系{Q}：O-xyz，三个坐标轴分别和坐标系{P}在初始位姿的三个坐标轴平行，且O'的投影点为O，Ai(i=1,2,…,6)为第i个支链丝杠与基座的连接点，Bi(i=1,2,…,6)为支链i上滑块的球铰中心，Ci(i=1,2,…,6)表示与运动平台连接的相应球铰的中心点.定长杆BiCi的局部坐标系为Oi-xiyizi，原点位于连杆的几何中心.设运动平台的位姿参数q=(x,y,z,α,β,γ)，其中x,y,z表示O点在坐标系{Q}中的坐标，α,β,γ 为运动平台欧拉角，则可得到坐标系{P}到坐标系{Q}的坐标转换矩阵为：

矩阵R为3×3的方向余弦矩阵，其每一列分别为坐标系{P}的x'、y'、z'轴在坐标系{Q}中的方向余弦.

2.2 动力学方程的建立

并联机器人的动力学方程具有如下的表示形式：

其中H(x)为n×n维对称的广义质量矩阵，C(x觶,x)为n×1阶的哥氏力及离心力矩阵，G(x)为n×1阶的重力矩阵，F为n×1阶的驱动力/力矩矩阵.由式中可以看出，机器人的动力学方程是一个时变、耦合的二阶微分方程，它表达了输入量(x咬,x觶,x)与输出F之间的非线性关系.经过牛顿－欧拉法对仿生机器马的动力学方程进行推导,可得仿生机器马的动力学模型可以写为如下形式:M

3 控制系统设计

在对仿生机器马进行动力学分析的基础上，进一步研究机器马的运动控制，由于机器马的动力学模型是一个多变量强耦合的非线性系统，因此需要合理设计控制器，把机器马转化为一个更加易于控制的系统.

机器马在仿生运动控制中，由于机械摩擦等干扰因素的影响，实际运动轨迹经常与期望轨迹之间存在偏差，控制系统必须纠正这些偏差，使机器马系统的实际运动能够跟踪期望轨迹，在这里我们设计如图所示的控制系统，包括一个外控制回路和内控制回路，外控制回路针对机器人的逆运动学模型采用比例微分控制策略，根据仿生机器马的实际轨迹与期望轨迹间的偏差进行负反馈控制.内控制回路根据机器人动力学特性进行动态补偿，使得经内控制回路作用后的机器人变为一个更易于控制的系统，化为一个解耦的线性系统，用于机器人线速度和角速度的控制.

通过轨迹规划得到仿生机器马在坐标系{Q}中的理论位置参数及姿态参数，可表示为：

则仿生机器马的位置误差为ep=x1-xv1，则

仿生机器马的实际姿态可以表示为：Rn=(n O a)，期望姿态为Rnd=(ndOdad).根据解出加速度法，定义机器人的姿态误差为：

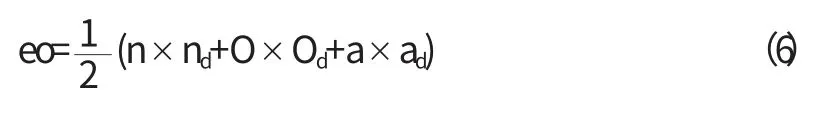
对式（6）求导，则e觶o=x觶2-x觶ω1，e咬o=x咬2-x咬ω1.则仿生机器马的位置误差与姿态误差以及误差的速度和加速度可以表示为以下形式：

在这里，将内控制回路根据动力学特性进行补偿，使得

对该线性定常系统引入的比例微分控制，则：可得系统闭环方程为：

式中Kd、Kp为调节参数矩阵，均为正定阵.

通过调节Kd和Kp可以获得理想地误差衰减规律，使得在控制过程中，总有(e觶 e)=(0 0)，实现轨迹跟踪.

由此可得设计控制器后的控制方程为：

由方程（9）中求得力F，然后带入仿生机器马的动力学方程中，即可求解仿生机器马的实际位置.

4 仿真实验

以仿生机器马并联机构为基础进行上述运动学与动力学模型仿真.参数如下：动平台长度为76cm，宽度为70cm，高度为4cm，重量为240kg，滑鞍质量为114kg，定长杆质量为9kg，定长杆杆长为30cm，令仿生机器马的运动平台作如下轨迹运动：沿y轴方向上作y=30sin(0.2pi*t)的正弦曲线，绕x轴做Anglex=pi/10*sin(0.2pi*t)的旋转，为了验证控制系统的性能，假设运动平台初始位置为（5，5，305），即实际起始位置与理论位置不重合，3个轴向的位置偏差均为5cm.Kd与Kp为对角阵，对角阵元素分别为10和100，仿真步长为0.01s.图中表示了3个轴向的偏差变化曲线.从曲线中可以看出，仿生机器马的3个轴向的偏差趋于零.从而验证了仿生机器马运动学分析和动力学模型的正确性，控制方法的可行性.

5 结论

从运动控制的角度，分析了仿生机器马的运动学模型，使用Newton-Euler方法建立了动力学模型，利用解出加速度法设计了非线性控制器对仿生机器马的轨迹跟踪进行控制.从控制的仿真结果可以看出：用文中的方法对仿生机器马的运动实施控制，可以使得机器人具有较强的抗干扰能力，准确实现对时变理论轨迹的跟踪.

〔1〕金振林.新型六自由度正交并联机器人设计理论与应用技术研究[D].秦皇岛:燕山大学,2002.

〔2〕黄真,赵永生,赵铁石.高等空间机构学[M].高等教育出版社,2006.

〔3〕Stefan, Staicu. Recursive modeling in dynamics of Agile Wrist spherical parallel robot [J] Robotics and Computer-Integrated Manufacturing. 2009.25(4):409-416.

〔4〕Peter Schwarz. Simulation of systems with dynamically varying model structure [J]. Mathematics and Computers in Simulation 2008.(79):850-863.

〔5〕韩佩富,赵立强.改进的6-DOF 并联机器人Newton-Euler 动力学模型[J].机器人,2002(22):315-318.

〔6〕申铁龙.机器人鲁棒控制基础[M].清华大学出版社,2000.