混凝土材料弹性模量快速识别技术＊

李唐樑 张开银 梅逸飞 范中林

（武汉理工大学交通学院1） 武汉 430063） （十堰市公路管理局2） 十堰 442000）

0 引 言

在混凝土桥梁结构（特别是旧桥）的静力分析中，通常采用的混凝土材料弹性模量设计值，较之其实际弹性模量值要小很多，影响了结构分析结果的可靠性．对于混凝土桥梁结构，常采用钻心测试方法来测量混凝土材料的弹性模量．此方法不但成本高，而且会造成桥梁结构的局部损伤．所以探寻一项有效、低成本、无损伤的混凝土构件真实弹性模量识别技术十分必要．

在复合材料理论中，认为混凝土的平均弹性模量与水泥砂浆、骨料的弹模、各成分的体积分数等因素有关［1］．文献［2］则提出了基于结构动力测试的大跨度混凝土桥梁弹性模量识别方法，利用所获得的桥梁动力特性，识别出结构的弹性模量．也有的研究从试验着手，把混凝土弹性模量看成是关于龄期的函数［3－4］，然后将试验数据拟合成各种计算公式，等等．本文的研究主要通过试验展开，经过对试验数据的处理和分析，并尝试从中寻找出合理的规律．

1 回弹测试原理

回弹测试法的原理［5］是：回弹仪中运动的重锤以一定的动能撞击顶在混凝土表面的冲击杆后，测出重锤被反弹回来的距离，即为回弹值（反弹距离与弹簧初始长度之比）．

当两物体碰撞时，按物体碰撞后变形的恢复程度（或能量损失），可分为完全弹性碰撞、弹性碰撞与塑性碰撞．由于被测混凝土构件是弹性体，在与重锤碰撞过程中伴随有能量损失，因此回弹仪重锤与被测混凝土构件的碰撞属于弹性碰撞．回弹仪测试混凝土构件过程的力学模型，可简化为一质量为m、半径为R的小球，至高h1处自由落下碰撞到混凝土构件后，并反弹至高度h2．设小球和混凝土材料的弹性模量分别为E1和E2，泊松比分别为μ1和μ2，v0为球与构件碰撞前的速度，反弹高度h2为［6］

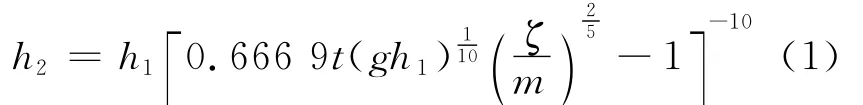
反弹高度h2就相当于回弹测试中的回弹值．式（1）表明：h2随碰撞时间t、混凝土材料参数E2、μ2不同而变化（其余的量皆为定量）．因此得知回弹值主要取决于混凝土材料的弹性模量和泊松比．

另外常用于推定混凝土构件抗压强度的还有超声法，若使用应力波理论分析超声法的工作原理不难得知［7］

式中：ρ为密度值；μ为混凝土构件泊松比；E为混凝土构件弹性模量；vl为声速值

式（2）表明：混凝土构件中的声速值vl也取决于混凝土材料的弹性模量．而实际操作时，不管是使用回弹法还是超声法，都会出现误差大等缺点，因而在检测混凝土抗压强度时，常采用超声法与回弹法联合测试抗压强度，结果误差比单一法小，适用范围广．但是由上述分析，声速值和回弹值都分别与弹性模量直接相关，因此若采用超声回弹综合法来推定混凝土构件弹性模量，会比用于推定抗压强度值效果好．另外若能得出较准确的弹性模量值，也能推测出较准确的抗压强度值．

2 回弹值－弹模关系曲线试验

2．1 试验的准备

按照规范要求制作C40和C50混凝土标准棱柱体试块各6块（部分试块见图1），试块尺寸为150mm×150mm×300mm．准备好测量精度符合试验要求的千斤顶、测力传感器、回弹仪、DH3818应变仪以及完好的应变片和必备试验工具，见图2～3．

图1 部分试件

2．2 试验的过程

图2 千斤顶和测力传感器

图3 设备整体布置

1）各取3个C40和C50混凝土标准棱柱体试块，用于测定混凝土试块的轴心抗压强度．将剩余的试块依次编号，在强度试验结束后，用于测定混凝土试块的弹性模量．

2）按试验要求贴好应变片，然后以全桥接入已调试好的应变仪，若更换应变仪测试通道时，则要修改灵敏系数．同时也将测力传感器布置好．

3）将千斤顶与试块安放好，调整对中，开始加荷至基准应力1MPa时的初始荷载值F0，读数时保持恒载60s并在30s以后记录每测点的应变．然后连续均匀地再加1MPa的荷载值F0，每增加一个F0读一次数，直至应力为轴心抗压强度的1／3荷载值Fa（10MPa）为止，每次读数保持恒载60s并在以后30s内记录每一测点的应变读数．用千斤顶加载时速度应均匀，不能过快．

4）用回弹仪在混凝土试件的4个侧面各弹击4个点并记录各点回弹值．测试回弹值时，应先将混凝土试块侧面磨平，避开上次弹击过的点和太靠近边缘的区域．

2．3 试验数据处理

通过记录的混凝土试件所受应力和相应的应变值，绘制应力－应变曲线，弹性模量即为所得应力－应变关系曲线的斜率．从测得的每1组回弹值中剔除最大最小值各2个，余下的用于计算平均回弹值R．见表1、表2．

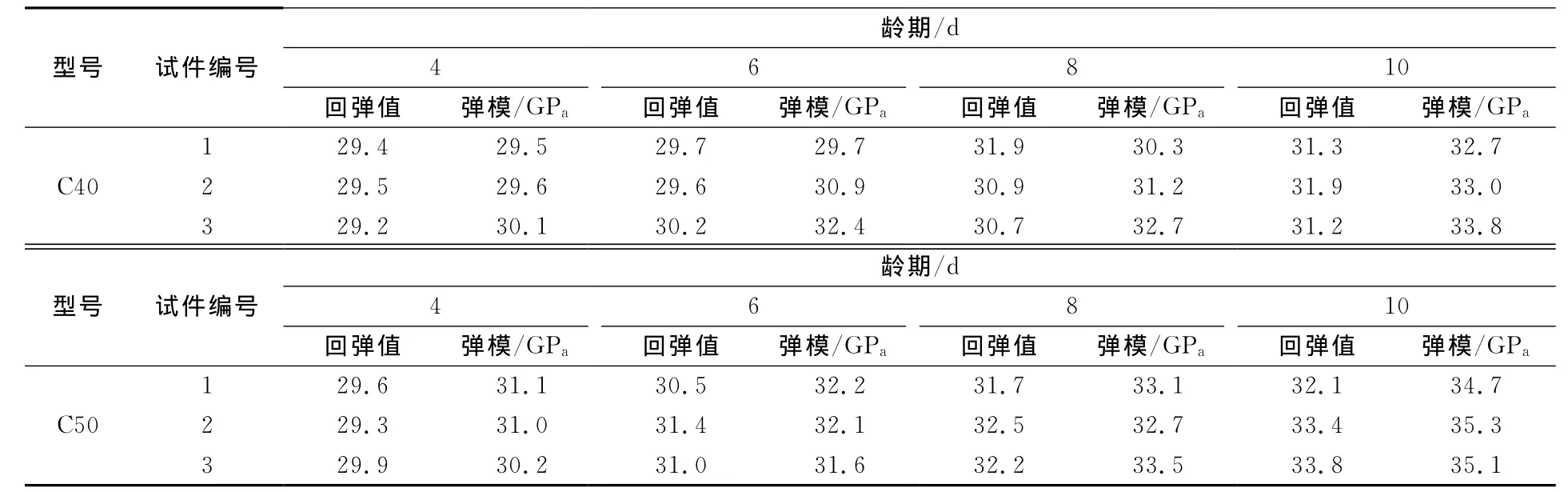
表1 各试件随龄期变化的回弹值与弹性模量值

表2 C40和C50对应龄期最终的回弹值和弹性模量值

C40和C50混凝土的弹性模量设计值分别是32．5GPa和34．5GPa［8］．从表2中可看出到第十d C40和C50混凝土的弹性模量试验值实际上已经超过它们的设计值，若在桥梁静力分析中继续采用偏小的弹模设计值，则分析结果不能客观的反应桥梁结构的整体性能和技术状况．

C40和C50混凝土10d内的回弹值－弹性模量关系曲线见图4～5．

图4 C40回弹值－弹性模量关系曲线

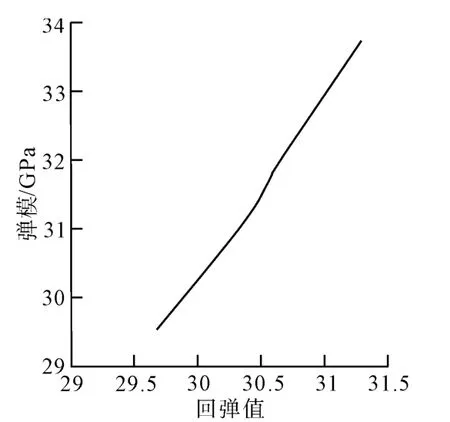
图5 C50回弹值－弹性模量关系曲线

2．4 试验结果分析

所处理得到的C40和C50回弹值和弹性模量值虽然略有偏小，但是也在正常的取值范围内．经过分析有些数据会出现较大误差的原因可能是：用千斤顶加荷时速度过快、试件的某一应变片没贴紧导致其变形滞后于混凝土变形．随着时间的推移C40和C50的弹性模量值还是呈现上升趋势的，只是比较养护较好时增加得慢一些，对试验结果影响不大．

混凝土回弹值－弹性模量关系曲线是随时间变化的．图中回弹值－弹性模量关系曲线为直线的原因与数据处理方法有关．后期的回弹值－弹性模量关系曲线未必会呈线性变化，而是会呈曲线发展．

由于时间、经费的关系，龄期在10d以后的混凝土回弹值和弹性模量值并没有来得及测试出来，试件的数量也很少，但是试验仍继续进行．虽然局限于各种因素，但是所得到的回弹值－弹性模量关系曲线是真实的．只要重复来做大量的试验，将混凝土各个型号的回弹值－弹模关系曲线做出来，汇总起来，在以后的工程中只需用回弹仪测出某一型号混凝土构件的平均回弹值，然后通过该型号混凝土的回弹值－弹模对应关系曲线，便能够较快速地将混凝土构件的实际弹性模量识别出来．对于有限元结构计算模型中材料参数的修正也会起到较大的帮助，从而可以保证桥梁结构整体性能和技术状况评价更加合理．

3 结 论

通过混凝土回弹测试机理的分析，从不同角度论证回弹值主要表征混凝土材料的弹性模量，并且通过试验，建立C40和C50两种型号的混凝土材料回弹值与弹性模量的关系，总结并得出以下结论．

1）通过对回弹测试方法的原理分析和应力波理论分析，证明了回弹值是一个与混凝土材料弹性模量有关的值．

2）利用回弹测试方法可快速、方便、可靠地测得混凝土桥梁结构的弹性模量，但是需要做大量的试验，测定各个型号混凝土材料相对应的回弹值—弹模关系曲线才能为实际工程所应用．

［1］肖建强．混凝土弹性模量的微分法预测［J］．山西建筑，2008，34（33）：55－58．

［2］赵永军．基于动力测试的高速铁路大跨连续梁桥混凝土弹性模量识别研究［J］．铁道标准设计，2010（1）：78－82．

［3］朱伯芳．再论混凝土弹性模量的表达式［J］．水利学报，1996（3）：68－72．

［4］王伟成，高利甲．几种混凝土弹性模量计算方法精度比较［J］．湖南工程学院学报：自然科学版，2011（4）：23－27．

［5］张俊平，姚玲森．桥梁检测［M］．北京：人民交通出版社，2002．

［6］蔡振岩，杨诚成．球与平板碰撞时间的理论计算及实测［J］．实验室研究与探索，1995（3）：101－104．

［7］李 昕．弹性与非弹性的测量和应用［M］．北京：冶金工业出版社，1999．

［8］中华人民共和国交通运输部．公路钢筋混凝土及预应力混凝土桥涵设计规范［S］．北京：人民交通出版社，2004．