预应力超高强混凝土梁抗弯性能试验研究＊

孟 刚 贾金青 刘春梅

（大连理工大学港口和近海工程国家重点实验室1） 大连 116024） （大连科诺科技发展有限公司2） 大连 116023）

0 引 言

超高强混凝土具有比强度高、负荷能力大、资源和能源消耗少、耐久性优异、可有效控制构件截面尺寸等特点［1］，特别适用于大跨、重载、高层和超高层结构中，随着超高强混凝土配置技术和施工泵送技术日益成熟，C100级超高强混凝土已逐渐应用于工程中［2］．但我国新修订的规范《混凝土结构设计规范》（GB50010－2010）［3］以及《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG D62－20040）［4］仅适用的混凝土强度等级为C15～C80，明显滞后于超高混凝土结构在实际工程中的应用，因此对超高强混凝土结构体系进行系统的研究是十分必要的．目前国内外对超高强混凝土柱、节点的受力性能研究较多［5－6］，但对超高强混凝土受弯构件的受力性能研究较少．本文以预应力筋位置和预应力筋配筋率为主要研究因素对预应力超高强混凝土简支梁进行了静力荷载下的抗弯性能试验，并通过有限元程序ANSYS对其进行了承载力数值模拟计算，并与试验结果进行比较．

1 试件设计和试验方案

1．1 试件设计

试验共对4根后张法预应力超高强混凝土简支梁进行张拉阶段的受力监测，梁长为4．0m，跨度为3．7m，截面尺寸为200mm×300mm，普通纵向受力钢筋采用HRB335级钢筋，箍筋为HPB235级钢筋，预应力筋采用1 860级高效低松弛钢绞线，张拉控制应力均为0．70fpfk（fptk为预应力筋抗拉强度标准值），预应力锚具采用低回缩锚具．试件梁的纵筋配筋均为AS＝3B18，A′S＝3B14，箍筋的配筋满足构造配筋，保证试件梁的弯曲破坏，支座处φ8＠50，剪跨段φ8＠150，纯弯段φ8＠200．试验梁配筋见图1～2，预应力筋配筋情况见表1．

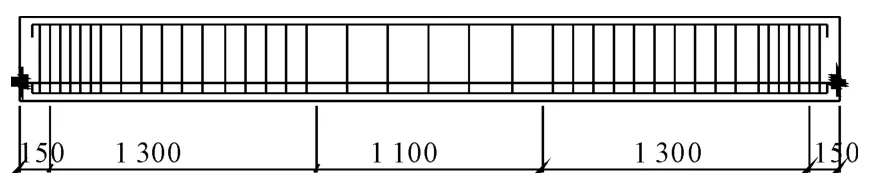
图1 试验梁配筋示意图（单位：mm）

图2 试验梁的截面示意图（单位：mm）

表1 试验梁预应力筋的设计参数

1．2 材料性能

试验梁超高强混凝土标准立方体抗压强度平均值fcu＝102．5MPa，标准棱柱体抗压强度平均值fc＝86．18MPa，弹性模量Ec＝38．7MPa，钢筋及钢绞线的屈服强度fy、极限强度fu及弹性模量实测值见表2．

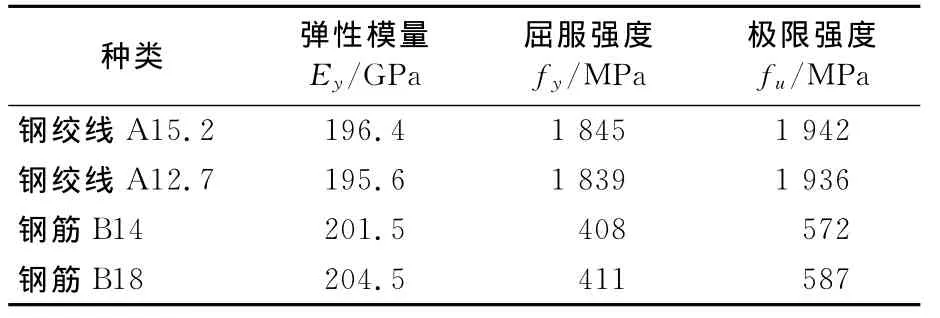
表2 钢绞线及钢筋实测力学性能指标

1．3 试验方案

试验均采用2点集中对称的同步分级加载方式．首先对试件进行预加载，调试仪器，然后卸载，将传感器、应变片和位移计调零；在试件开裂前，每级所加荷载约为0．05 Mu（Mu为跨中极限弯矩），持载10min；试件开裂后每级所加荷载约为0．1 Mu，持载10min；试件达到屈服荷载后加载幅度恢复至0．05 Mu，直至试件达到极限荷载破坏．荷载由10 000kN试验机在分配梁上施加，并通过荷载传感器测量施加荷载的大小；跨中梁底设置位移传感器测量试件的挠度；沿试件跨中截面高度方向布置混凝土应变片以及纯弯段纵筋、钢绞线表面布置应变片；荷载、位移传感器和应变片数据通过IMC系统自动采集，跨中纯弯段长度为1 100mm，试验加载方式见图3．

2 试验现象与试验结果分析

2．1 试验现象

图3 试验梁加载图

在加载初期，试验梁的荷载挠度曲线基本呈线性变化，当荷载达到0．3 Mu（弯矩为50kN·m）左右时，首先在试验梁纯弯段下边缘出现竖向弯曲微裂缝；随着荷载的增加，由于钢筋和混凝土的粘结与应力传递，裂缝数量增加，裂缝间距均匀，一般9～11mm之间；当荷载达到0．6 Mu（弯矩为105kN·m）左右时，纯弯段新裂缝基本不出现，原有裂缝宽度扩展并向上延伸；当荷载达到0．75 Mu（弯矩为130kN·m）左右时，剪跨段出现多条裂缝，间距均匀，并由梁下边缘向加载点倾斜延伸，纯弯段裂缝继续向上延伸扩展，跨中最大裂缝宽度0．2mm；荷载继续增加，达到0．85 Mu（即弯矩为148kN·m）左右时，试验梁屈服，受压区混凝土压裂，并伴随有混凝土崩裂声音，新裂缝不再出现，纯弯段裂缝继续向上扩展，剪跨段裂缝继续向加载点倾斜扩展，最大裂缝宽度0．68mm．当荷载临近极限弯矩Mu时，裂缝发展加快，跨中挠度增加迅速，纯弯段受压区混凝土在受压筋位置附近出现水平裂缝，最终受压区混凝土压碎，梁达到极限状态，试验梁均呈现弯曲破坏形态．由于超高强混凝土脆性大，试验梁达到极限承载力后，承载力迅速降低．试件梁破坏形态见图4．

图4 试验梁弯曲破坏形式及裂缝分布情况

2．2 试验结果分析

2．2．1 荷载－挠度曲线

图5为各试验梁跨中截面荷载－挠度曲线．由图5可见，荷载达到极限荷载的30%之前，跨中截面的挠度基本呈线性增长趋势，试验梁处于弹性阶段；随后曲线出现第一个拐点，在极限荷载的30%～85%之间，挠度增长速度加快，试验梁进入弹塑性阶段；达到极限荷载的85%以后，荷载增加变缓，挠度迅速增张，受拉纵筋屈服，试验梁进入屈服阶段，屈服点较为明显；达到极限荷载后，承载力迅速降低，挠度增长较缓．试验梁中均配置了一定数量的受压纵筋，在一定程度上改善超高强混凝土材料脆性破坏特点，使得荷载－挠度曲线达到极限荷载之后位移略有增加，由此得出增大受压纵筋的配筋率有利于改善超高强混凝土梁的脆性破坏情况．

图5 跨中截面荷载位移－挠度曲线

2．2．2 设计参数的影响

1）预应力的施加能够有效的控制构件的开裂和挠度，试验梁L1～L4屈服时最大裂缝宽度依次为0．48，0．6，0．68，0．52mm．由此得出，预应力筋高度hp以及预应力筋配筋率对裂缝开展有一定影响，hp越小，试件屈服时最大裂缝宽度越小，试件L1比试件L3减小29．4%；预应力筋的配筋率越大，试件屈服时最大裂缝宽度越小，但对试件抗裂性影响不明显．

2）对于超高强混凝土梁，预应力筋高度hp越大，梁的屈服段越长，梁的延性越好；预应力筋配筋率越大，梁的屈服段较短，梁的延性越差．

3）表3为试验梁的开裂荷载、屈服荷载和极限荷载．由此可见，在相同的预应力张拉应力的情况下，试件L1～L3的预应力筋高度hp越小，预应力筋提供的反弯矩越大，试件的开裂荷载越大，试件进入消压状态以后，计算正截面弯矩平衡时，预应力筋提供的弯矩越大，屈服荷载和极限荷载就越大；相同预应力筋高度条件下，预应力筋配筋越大，试件中和轴高度越小，混凝土受压区越小，试件的开裂荷载、屈服荷载和极限荷载越大．

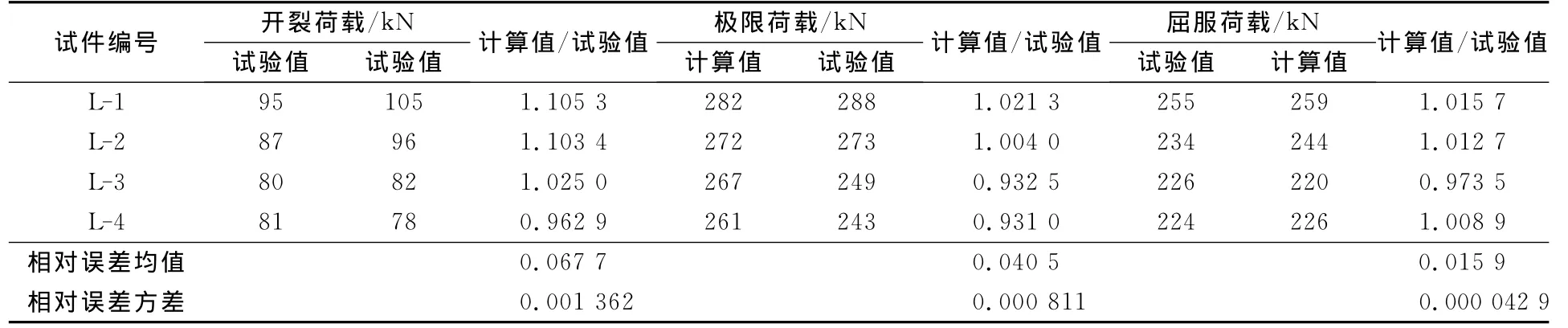
表3 试验结果与计算结果对比

3 预应力超高强混凝土梁承载力有限元计算分析

本文采用ANSYS有限元程序对预应力超高强混凝土梁在静力荷载作用下的抗弯受力过程进行数值模拟分析，采用蒲心诚［7］提出的超高强混凝土本构模型，其单轴受压情况下，不同强度等级的混凝土的应力应变上升段关系式为

式中：fcu，100为试件尺寸为100mm×100mm×100mm的立方体抗压强度；k为修正系数；ε0为峰值应变．

修正系数k按k＝0．494 7infcu，100－1．577 1

峰值应 变ε0＝ （8．505 5fcu，100＋123 0）×10－6

fcu，100和标准立方体试块抗压强度fcu之间的换算关系以及标准棱柱体试件轴心抗压强度fc与标准立方体试块抗压强度fcu的换算关系为［7］

在ANSYS分析中，混凝土采用SOLID65单元进行模拟，在计算中不考虑形函数的附加项，便于收敛．纵筋、箍筋以及预应力筋采用空间二节点杆单元LINK8进行模拟［8］．混凝土采用多线性随动强化模型（KINH），破坏准则采用默认的 William－Warnker五参数破坏准则［9］．钢材（工字钢、纵筋、箍筋以及预应力筋）单轴应力－应变关系采用二折线理想弹塑性模型．支座钢垫块和锚具垫块采用弹性模型，弹性模量取钢材的10倍．ANSYS中钢材强化模型采用双线性随动强化模型（KBIN）．

对4根试验梁进行ANSYS数值模拟，采用2点对称位移加载，控制子布，控制计算精度，4根试验梁均收敛良好．

4 结 论

1）超高强混凝土梁具有较高的承载力，由于超高强混凝土材料的脆性问题，导致极限荷载后持载能力较差．

2）在超高强混凝土梁中施加预应力，较好的抑制了裂缝的开展，控制了裂缝的宽度，改善了超高强混凝土梁正常使用阶段的使用性能．

3）预应力筋高度hp和预应力筋配筋率对超高强混凝土梁受力性能有较为显著的影响，当hp较大或者相同预应力筋位置配筋率较小时，能够使超高强混凝土梁保持较高的承载力的同时，延长超高强混凝土梁屈服阶段，提高梁的延性性能，改善其受力性能．

4）本文采用ANSYS有限元程序对预应力超高强混凝土梁承载力进行数值模拟计算，计算结果与试验结果吻合较好，为预应力超高强混凝土梁受力性能分析提供了一种较为准确的数值计算方法．

［1］蒲心诚．超高强高性能混凝土［M］．重庆：重庆大学出版社，2004．

［2］JOSEF H，CLAUS G．Structural behavior of partially concrete encased composite sections with high strength concrete［J］．ASCE Conf．Proc，2006，186（33）：346－355．

［3］中交公路规划设计院．JTG D62—2004公路钢筋混凝土及预应力混凝土桥涵设计规范［S］．北京：人民交通出版社，2004．

［4］中交公路规划设计院．GB50010—2010混凝土结构设计规范［S］．北京：人民交通出版社，2010．

［5］贾金青．钢骨高强混凝土柱的力学性能［M］．大连：大连理工大学出版社，2006．

［6］YAN Changwang，WANG Haitao，MENG Gang．Seism ic performance of steel reinforced ultra highstrength concrete columns［J］．Journal of SinChuan University：Engineering Science Edition，2009，41（3）：216－222．

［7］张谢东，王勇威，蒲心诚，等．单轴压力56．3～164．9 MPa混凝土的应力－应变关系［J］．建筑结构学报，2005，26（1）：97－102．

［8］王文炜，李 果，韩武钦．FRP加固钢筋混凝土梁非线性有限元分析［J］．武汉理工大学学报：交通科学与工程版，2007，31（2）：235－238．

［9］毛 伟，贾金青，余 芳．分离模型预应力混凝土梁数值模拟［J］．铁道建筑，2011（7）：17－19．