大规模油藏数值模拟的块压缩存储及求解
2013-01-15王宝华吴淑红韩大匡桓冠仁李巧云李小波李华周久宁
王宝华,吴淑红,韩大匡,桓冠仁,李巧云,李小波,李华,周久宁
(1. 中国石油勘探开发研究院;2. 提高石油采收率国家重点实验室;3. 中国石油大学(北京))
0 引言
油藏数值模拟利用已知油藏地质参数及动态开发数据再现油藏开发历史、预测油藏开发趋势、制定或调整开发方案[1-3],已成为油田开发研究必不可少的技术手段。油藏数值模拟的数学模型由多个非线性偏微分方程耦合而成,具有强非线性、强间断性、强耦合性,求解这些微分方程组的时间通常占整个模拟时间的 70%~80%,随着模型规模和复杂程度的增加,该比例还会增加,如何高效求解这些微分方程组成为数值模拟的核心问题[4-5]。
目前,中国新开发油田中低渗、特低渗储量比例高(约占60%~70%),已开发主力油田进入高含水、高采出程度的开发后期[6-7],油藏开发难度加大。为了进一步获得经济有效的产量,需深化油藏描述,建立更精细的油藏数值模型[8-9],这些模型比以往的地质模型网格数更多、生产历史更长、井的数目和措施更多、油气分布更为复杂,极大地增加了油藏数值模拟历史拟合和调整方案开发趋势预测的工作量、难度并更耗时[10]。为了提高数值模拟效率,本文针对油藏模拟中最常用的黑油模型,研究大规模稀疏系数矩阵的压缩存储及求解方法。
1 基础模型
黑油模型中油、气、水3相基本微分方程为:

各相压力和毛细管压力有关,定义为:
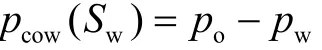

式中 K——渗透率,10−3μm2;φ——孔隙度,%;Krw,Kro,Krg——水相、油相、气相相对渗透率,f;μw,μo,μg——水相、油相、气相黏度,mPa·s;ρw,ρo,ρg——水相、油相、气相密度,g/cm3;ρo,o——油相中油组分的密度,g/cm3;ρg,o——油相中气组分的密度,g/cm3;Sw,So,Sg——水相、油相、气相饱和度,%;t——时间,s;pw,po,pg——水相、油相、气相压力,MPa;g——重力加速度,m/s2;Z——深度,m;pcow,pcgo——油水、气油界面毛管压力,MPa。
假设三维模型横向上有nx个网格,纵向上ny个网格(每个平面上有nxy个网格,nxy=nxny),垂向上有nz个网格,模型总网格数为n(n=nxnynz),在按行自然排序的块中心网格上,利用控制体积全隐式求解格式离散黑油模型(1)式—(3)式,得到 n阶带状稀疏系数矩阵:

其中

式中 B,C,D——组分差分方程中水饱和度、油饱和度和油相压力 3个变量在相关有效节点上的系数;下标:w,o,g——水、油、气组分。
根据黑油模型的数学特性,将具有抛物方程性质的油相压力方程和具有双曲型方程性质的饱和度方程结合在一起,以块形式进行运算能够避免小扰动对模拟问题的干扰,增强稳定性,减少迭代次数,提高模拟速度。随着油藏模拟规模的增加,稀疏系数矩阵中零元素大量增加,远超过非零元素的数目,稀疏矩阵存储方式决定了内存的消耗量,直接影响运算时间。
2 块压缩存储格式
油藏数值模拟中采用的压缩存储格式有很多,如点的坐标压缩存储、行压缩存储、修正行压缩存储、对角线压缩存储及由点的行压缩存储演化出的块行压缩存储等[2,11]。本文主要研究块的压缩存储格式,主要由有效节点压缩存储和块压缩存储两部分构成,与行压缩存储格式相比,块压缩存储格式能够节约更多的内存,减少非零元素的搜索次数。
2.1 有效节点压缩存储技术
在实际油藏模型中,地层中存在大量死结点(如孔隙度为零),据此特点,在稀疏矩阵压缩存储时,只存储有效节点上的相应信息从而达到矩阵降阶、节约内存的目的。以一个3行3列的二维网格为例,其中第5、6、8、9这4个节点为有效节点,其余为死节点(见图1a),若全部存储,三变量黑油模型的系数矩阵将达到27阶;若将这4个有效节点重新排序(见图1b),则黑油模型系数矩阵降至12阶。
为将此系数矩阵降阶,定义压缩排列数组:


图1 自然排序(a)和有效节点排序(b)的二维网格
其中 S =(J−1)Nx+I
式中 N——压缩排列序号,1≤N≤ne;ne——有效节点总数;Nc——有效网格节点映射;S——常规排列序号;J——纵向网格序号,1≤J≤ny;I——横向网格序号,1≤I≤nx;nx,ny——横、纵方向的网格总数。
利用(6)式将常规排列中的死节点去除并将有效节点重新排序(见表 1),死节点置 0,有效节点按自然顺序排列。

表1 有效节点排序表
利用上述方法压缩有效节点能够大幅降低稀疏系数矩阵的阶数,节约模拟内存,如中国东部某陆相非均质油田数值模型中,总结点数约 40×104,有效节点数约14×104,若全部存储需要0.200 GB的内存,若用本文压缩排列方法只需 0.065 GB的内存,节约了近70%的内存空间。
2.2 块压缩存储技术
有效节点压缩存储虽然能有效减少内存的损耗,但压缩后的稀疏矩阵中仍含有大量的零元素。考虑到多变量黑油模型的特点,本文以块为单位存储系数矩阵中的非零元素,根据矩阵中非零块元素(块中有一个非零元素即认为是非零块元素)的位置对称性,只记录下三角矩阵非零块元素的地址。本文采用 3个双精度指针数组 E、T及 Tʹ分别存储系数矩阵中的对角线块元素、下三角块元素及上三角块元素,并利用 3个整型数组记录非零块元素的地址,实现稀疏矩阵块压缩排列:①Nco(SI),下三角矩阵中每行非零块元素的总数(SI为块行号);②Nod(SI):下三角矩阵中每块行第1个非零块元素的位置序号;③Icn(SR):下三角矩阵中非零块元素对应的列序号(SR为非零块元素的累计计数序号)。经有效节点压缩后,黑油模型(1)式—(3)式离散形成如下形式的矩阵(以 4阶矩阵为例):

A中各元素为如(5)式所示的3阶子阵。利用块压缩存储格式,矩阵 A的存储见表 2,各元素按行依次存储。

表2 矩阵A的块压缩存储表
非零块元素的地址由数组Nco、Nod及Icn记录(对应于下三角压缩存储数组T),见表3、表4。

表3 块压缩存储的Nco和Nod数组

表4 块压缩存储的Icn数组
2.3 不同压缩存储方法存储量及搜索次数对比
2.3.1 存储量对比
不同压缩存储格式存储稀疏矩阵非零元素所需的数组长度大致相同,但记录非零元素地址的数组差别很大,如行压缩存储格式存储稀疏矩阵需要3个数组:1个实数型数组存储稀疏矩阵的非零元素,2个整型数组分别记录相应非零元素行和列的位置,若 n阶稀疏矩阵中非零块元素个数为 nt,其中每个非零块元素均为3阶子矩阵,则该压缩格式所需存储空间为:9ntLd+(3n+1+9nt)Lint,其中 Ld为一个双精度数长度(8 B),Lint为一个整数的长度(2 B);对于相同的n阶nt个非零 3阶块元素的稀疏矩阵,按本文提出的块压缩存储需要存储空间:9ntLd+ [(3n + nt)/2+1] Lint;若不利用压缩存储格式需要的存储空间是n2Ld。以三相黑油模型在不同有效网格上形成的系数矩阵为例,块压缩存储比行压缩存储耗费内存少,且矩阵规模越大节约的内存越多(见表5)。

表5 块压缩存储、行压缩存储及非压缩存储占用的内存
2.3.2 搜索次数的对比
在模拟中,对于非零元素的搜索,块压缩存储远远少于行压缩存储,以n阶nt个非零3阶块元素的稀疏矩阵为例,在行压缩格式中需要搜索 9nt个非零元素,而在块压缩格式中只需搜索下三角矩阵中非零块元素,即只需搜索(nt−n)/2个非零块元素,行压缩存储需要的搜索次数大约是块压缩存储的 18nt/(nt-n)倍。仍以三相黑油模型在不同有效网格上离散的系数矩阵为例,块压缩存储需要搜索的非零元素个数远少于行压缩存储,大约只有行压缩存储的5%(见表6)。

表6 块压缩存储、行压缩存储非零元素搜索次数
3 块广义极小余量 GMRES预处理迭代法
三维三相黑油模型(1)式—(3)式离散后形成大规模稀疏线性方程组,求解这些线性方程组大约占整体模拟时间的80%左右,而且随着模拟规模的增加,该比例还会增大。目前求解大型稀疏矩阵较为成熟的方法是预处理迭代方法,如不完全LU分解(incomplete LU factorization)预处理广义极小残量迭代法(generalized minimal residual method,GMRES),该算法利用 Krylov子空间矢量的最小残量进行迭代求解,具有收敛速度快、稳定性好等优点[12-13]。由于油藏问题中的系数矩阵一般很难满足点的对角占优性,本文考虑以节点为单元进行ILU分解GMRES迭代。
3.1 块不完全LU分解
块不完全LU分解就是预定分解矩阵L、U的非零指标集G,在块LU分解中置G以外子块为零,形成系数矩阵A的近似分解:A(G)=L(G)U(G)[14]。前文中已将形如(4)式的带状矩阵 A = (aij)n×n的主对角、下三角及上三角非零块元素分别存入E、T、及T ʹ数组中,利用这3个数组对A进行块LU分解时只有A的非零元素参与计算而且不产生新的非零元素,如此计算得到的L、U矩阵为A的块不完全LU分解,具体计算步骤如下。
①令m=1;
②将对角线上第m个块矩阵进行标准化处理,分解为上三角块与下三角块的乘积,下三角块中的元素lji与上三角块中的元素uij由下式计算:

其中,Cij为块对角矩阵的元素。
③对3阶子阵T及T ʹ中的元素进行与第1步类似的计算,得到相对应的L、U矩阵中的子阵的值;
④令m=m+1,返回②直至m=n。
3.2 块广义极小残量迭代(GMRES)法
设 n阶线性方程组 Ax=b(A如(4)式,其元素 aij如(5)式,x为未知量,其初始近似解向量为x0,第l次迭代的近似解向量为xl,相应的残差为rl=b−Axl,l=0,1,…。GMRES算法是通过求使 rl极小的xl∈κl来逼近Ax=b的精确解,其中κl为Krylov子空间:为首次残差,设Vl=(v1,v2,…,vl)为κl的标准正交基,且AVl=Vl+1Hl,其中Hl为上Hessenberg矩阵,xl可写成xl=Vlyl(yl为l维向量),则rl的极小值问题转化为极小问题:

其中02||||β=r,e1=(1,0,0,…,0)ʹ[13]。这种基于Krylov子空间的迭代法收敛速度快、精度高且稳定性好,块GMRES预处理迭代法的一般流程如下。
①计算r0=M−1(b−Ax0),此处M=LU是A的ILU分解阵,以及标准正交基第1个元素10β=vr,其中矩阵每个块aij与向量块xj的乘积如下:

②循环 j=1,2,…,l;
③计算 wj=M−1Avj;
④对于i=1,2,…,j,计算Hessenberg矩阵中的向量 hij=(wj, vi);
⑤计算Hessenberg矩阵中的向量hj+1,j= | |wj||2和vj+1=wj||wj||2;
⑥更新xl=x0+Vlyl,其中yl满足(7)式;
⑦如果收敛,停止循环;否则,令x0= xl,返回①。
步骤②—⑥中矩阵与向量的乘积及向量与向量的运算均为块矩阵之间的运算。
4 大规模水驱油藏算例模拟
国际黑油模型标准考题SPE10描述了大规模严重非均质水驱油藏的生产动态,是反映油藏数值模拟技术的规模化、计算精度和计算速度的重要考题。该算例为油水两相模型,油藏埋深为3 657.6 m,初始油藏压力41.37 MPa,地面油密度、气体密度及地面水密度分别为 0.849 g/cm3、1.000×10−4g/cm3及 1.024 g/cm3,地层水及地下原油体积系数均为 1.01,水和岩石压缩系数分别为 4.41×10−5MPa−1和 1.47×10−5MPa−1,水及地下原油黏度分别为0.3 mPa·s和3.0 mPa·s。
在 SPE10算例中渗透率的最大值为 20 000×10−3μm2,最小值为 0.000 66×10−3μm2,平均值为364.52×10−3μm2,油层渗透率极差为 23.3,垂向与平面渗透率的比值变化较大,其中,河道为0.3,基底的为 0.001。该算例中孔隙度最大值为 0.5,平均值为0.174 9,部分单层孔隙度见图2。

图2 SPE10算例部分单层孔隙度分布
SPE10模型模拟的是366 m×671 m×51.85 m范围内1口注水井和4口生产井的开发动态,总节点数为1 122 000。在处理器为Intel Xeon X5660 2.80GHz的计算机上用块GMRES预处理算法、商业模拟器A及B模拟SPE10算例的日产油、综合含水和地层压力等生产指标曲线(见图 3),可见,该算法的计算精度与商业油藏数值模拟器基本一致。在该计算机上,块GMRES预处理算法、商业模拟器A及B模拟SPE10算例的总耗时分别为21.5 h、24.3 h和101.3 h,计算速度较快。说明块 GMRES预处理算法能够快速实现大规模的油藏数值模拟,结果可靠,具有较强的实用性。

图3 SPE10全油田日产油、综合含水及地层压力曲线
图4 为采用块GMRES预处理算法模拟SPE10算例得到的不同时间段注采井间水线推进剖面。该方法可以精确模拟注水过程中水线推进到油藏并逐步到达油井的过程,对于严重非均质油藏,可以清晰地分析描述注入水在不同渗透层推进的速度以及沿高渗透层和高渗区域的指进过程。

图4 SPE10算例在不同时刻含水饱和度分布(P1、P3为生产井,I1为注水井)
5 结论
针对三相黑油模型模拟时形成的大规模稀疏系数矩阵,提出了有效节点压缩和块压缩存储相结合的存储格式,分别采用3个实数组和3个整型数组存储稀疏矩阵的非零块元素及其地址信息,减少了内存的占用并降低了计算时的搜索次数。
在求解黑油模型的稀疏线性方程组时,先用块ILU分解改善系数矩阵的特征值分布,得到性质更好的矩阵,再用块 GMRES算法求解改良的线性方程组。由于黑油模型的系数矩阵具有块对角占优性质,块GMRES预处理法具有良好的稳定性和收敛性,能够快速、精确实现大规模油藏数值模拟。
块压缩存储与块 ILU GMRES算法相结合可模拟大规模油藏的生产动态,计算结果与商业软件基本一致,速度较快且耗费内存较少,是一种高效、可靠的求解技术。
[1] 韩大匡, 陈钦雷, 闫存章. 油藏数值模拟基础[M]. 北京: 石油工业出版社, 1999: 34-44, 241-242.Han Dakuang, Chen Qinlei, Yan Cunzhang. The basis of reservoir simulation[M]. Beijing: Petroleum Industry Press, 1999: 34-44, 241-242.
[2] Chen Zhangxin, Huan Guanren, Ma Yuanle. Computational methods for multiphase flows in porous media[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2006: 1-2.
[3] Kazemi A, Stephen K D. 油藏数值模拟自动历史拟合方法: 以Nelson油田为例[J]. 石油勘探与开发, 2012, 39(3): 326-337.Kazemi A, Stephen K D. Schemes for automatic history matching of reservoir modeling: A case of Nelson oilfield in the UK[J].Petroleum Exploration and Development, 2012, 39(3): 326-337.
[4] Li Xiaobo, Wu Shuhong, Song Jie, et al. Numerical simulation of pore- scale flow in chemical flooding process[J]. Theor. Appl. Mech.Lett., 2011, 1(2): 022008.
[5] Wang Baohua, Lü Shujuan, Lu Qishao, et al. Long time behavior of finite difference solution for a semilinear parabolic equation[J].DCDIS-A, 2007, 14(S2): 141-147.
[6] 纪淑红, 田昌炳, 石成方, 等. 高含水阶段重新认识水驱油效率[J]. 石油勘探与开发, 2012, 39(3): 338-345.Ji Shuhong, Tian Changbing, Shi Chengfang, et al. New understanding on water-oil displacement efficiency in a high water-cut stage[J]. Petroleum Exploration and Development, 2012,39(3): 338-345.
[7] 李巧云, 张吉群, 邓宝荣, 等. 高含水油田层系重组方案的灰色决策优选法[J]. 石油勘探与开发, 2011, 38(4): 463-468.Li Qiaoyun, Zhang Jiqun, Deng Baorong, et al. Grey decision-making theory in the optimization of strata series recombination programs of high water-cut oilfields[J]. Petroleum Exploration and Development, 2011, 38(4): 463-468.
[8] Wu Shuhong, Han Min, Ma Desheng, et al. Streamflooding to enhance recovery of a waterflooded light-oil reservoir[J]. JPT,2012(1): 64-66.
[9] 韩大匡. 关于高含水油田二次开发理念、对策和技术路线的探讨[J]. 石油勘探与开发, 2010, 37(5):583-591.Han Dakuang. Discussions on concepts, countermeasures and technical routes for the redevelopment of high water-cut oilfields[J].Petroleum Exploration and Development, 2010, 37(5): 583-591.
[10] 邹存友, 常毓文, 王国辉, 等. 水驱开发油田合理油水井数比的计算[J]. 石油勘探与开发, 2011, 38(2): 211-215.Zou Cunyou, Chang Yuwen, Wang Guohui, et al. Calculation on a reasonable production-injection well ratio in waterflooding oilfields[J].Petroleum Exploration and Development, 2011, 38(2): 211-215.
[11] 成谷, 张宝金. 反射地震走时层析成像中的大型稀疏系数矩阵压缩存储和求解[J]. 地球物理学进展, 2008, 23(3): 674-680.Cheng Gu, Zhang Baojin. Compression storage and solution of large sparse matrix in traveltime tomography of reflection seismic data[J].Progress in Geophysics, 2008, 23(3): 674-680.
[12] Saad Y, Gmres M S. A generalized minimal residual algorithm for solving nonsymmetric linear systems[J]. Siam J. Sci. Stat. Comput.,1986, 7(3): 856-869.
[13] Li Wenjun, Chen Zhangxi, Richard E E, et al. Comparision of the GMRES and ORTHOMIN for the black oil model in porous media[J].Int. J. Numer. Meth. Fluids., 2005, 48(5): 501-519.
[14] 林小兵. 二维多相油藏数值模拟的 BILUCG算法[J]. 石油勘探与开发, 1987, 14(1): 76-84.Lin Xiaobing. BILUCG algorithm for 2-D multiphase reservoir simulation[J]. Petroleum Exploration and Development, 1987, 14(1):76-84.
