基于概念决策模型的油气勘探模拟——以伊朗西南部德兹夫尔海湾为例

Soleimani M

（伊朗沙赫鲁德理工大学采矿、石油与地球物理系）

0 引言

类比法广泛应用于地质研究中，在矿藏资源潜力预测和勘探决策方面也有一定应用。新区开始勘探研究时，地质家首先会研究区域地质条件，将过去勘探工作中所积累的经验作为类比信息。在地质家看来，不同区域通常具有不同的地质特征，反映了沉积和区域地质的独特性。如果研究区与类比区存在差异，且类比区之间存在差异，最简单的方法是将每个地区划归一个不同的种类。但这种观点存在一些局限[1]，其主要原因在于采样和获得勘探信息的成本很高，特别是在石油勘探中（如果勘探目标区很大，该成本将会非常高）；原因之二，与第1个因素有关，即，由于直接采样成本高昂，间接采样方法如地质研究被广泛用于推测未知矿藏资源状况和勘探结果；原因之三，亦与第 1个因素相关，高昂的采样成本突显了获知相关随机变量先验分布的重要意义[2]。因此，如果根据地质特征类比作出决策，设计勘探项目（随后将进行钻探），可能面临高额的投资损失。当类比区和研究区存在地质差异时，可采用以下3种方法避免这种损失[2]：①将各个地区分别作为限制因素和先验概率来源，应用决策理论计算其他替代方案的预期损失；②从专家处获取主观的先验概率，获得主观概率的最佳准备工作是审查支持性信息，通常包括矿物/石油产状以及类似地区的矿藏信息，而由地质家根据经验和知识对不相似性作出判断；③对类比区与研究区的地质相似性进行定量评估，提供矿物/石油产状的数学类比信息。本文基于地质背景的相似性原则，选用第 3种解决方案，提出伊朗境内部分区域油田勘探的概念决策模型。

1 模型整体结构

图1 基于概念决策模型的油气勘探模拟示意图

设计概念决策模型的目的是根据地质假设（构造圈闭，地下构造和地层圈闭）模拟盆地勘探。模型中除需选择目标盆地的地质假设条件外，还需指定勘探方法和调查强度（见图 1）。具体决策包括是否开展普查勘探、是否钻井、是否采用新的地质假设或终止勘探等。发现油气藏的工作包括在预测的油藏区域内钻井，钻井深度与油层深度相同，或大于油层深度。模型中采用贝叶斯决策理论进行决策，因而决策可反映下列期望值：油藏数目及其规模的分布；一种地质假设相对于另一种地质假设的期望成功率；每种地质假设条件下使用勘探方法探测和识别出地质条件的概率。根据贝叶斯决策理论，将根据勘探结果对一些初始期望值进行修改。模型参数包括了经济因素（价格、勘探和生产成本、产量、贴现率、预算和税费等），在每种地质假设条件下，经济参数与油藏参数均保持不变[3-4]。

概念决策模型由 4个主要部分构成：①特性的生成，根据假设，确定盆地异常点种子、油藏位置种子及各种假设条件下每个油藏的响应矢量种子等信息；②勘探模拟，按照假设开展地质普查；③决策分析，随着信息不断丰富，修改先验概率，并计算钻井、非钻井和勘探的预期损失；④经济评价，评价所发现油气藏的净现值，并确定各经济油藏的产量。

图 1所示为模拟的主要阶段和次序。该模型的每一次迭代计算都要先生成特性、含油气盆地，然后模拟盆地勘探。对所获得的结果进行处理，得出所选定的量值，如所发现的油气藏储量及给定经济参数条件下的经济可采储量[5]。通过改变选定参数及其取值水平重复模拟，可检验模型的敏感性[6]。

2 特性模拟

特性模拟的第 1步是把地表预测的含油异常区作为盆地的种子，异常区随机散布于整个盆地，其面积由抽样分布频率确定（见图2a）。图2b所示为某个地质假设条件下异常区的空间分布，异常区位置由随机选定，其规模分布由取样确定。一旦确定了异常区的种子，可通过矩形分布抽样得到概率（P），并与油藏数目占异常体总数的假设比例进行对比，从而确定与油藏有关的异常，即：若 P ＜NpNa，则为油藏，其中Np为油藏个数，Na为异常区个数。

对于确定为油藏的每个异常区，异常区面积可转换成最终油藏储量[7]。实际勘探中，勘探技术并不能探测出全部异常，有下列两种情况[8]：如果采用的勘探方法无效，则不可能识别出特定类型的含油异常；勘探方法对于特定类型的异常有效，但由于解释有误或局部存在地质干扰，也可能无法识别出异常。

3 伊朗油田的地质条件响应

通过具有响应矢量的每个异常区种子，将上述两种情况和伊朗油田实际地质条件引入到模型中。响应矢量的元素为特定假设下地质条件对各种勘探方法的响应[7]，元素随异常体类型的变化而变化。以伊朗西南部油田为例，模拟3种模型（圈闭）的油气资源潜力：地表构造圈闭、地下构造圈闭和地层圈闭[9]（见表1）。当对某一勘探技术的响应小于100%时，从矩形概率分布进行抽样，并将其与表 1的相应响应值进行对比，就可以确定出该勘探技术的响应。例如，地下构造对重力勘探的响应为 20%，由此得出假设地下构造异常的重力响应值为 P＜20%[10-12]。每次微迭代计算都要重新确定盆地异常区种子，根据深度和地质假设，结合表1中6种勘探方法中每一种方法的每个异常勘探响应，生成异常区和油藏的空间分布。确定盆地异常区种子后，进入盆地勘探模拟阶段。这种勘探模拟需要模拟给定勘探方法和地质假设条件下的勘探过程，还需要模拟地质家和勘探家的决策过程[10]。

图2 异常区规模及空间分布示意图

表1 地质条件与勘探方法的响应关系

图3 研究区位置图

伊朗西南部德兹夫尔海湾（见图3）是伊朗西南油气区的中心，伊朗主要油田均分布于该区。虽然该地区资源潜力巨大，至今实施的勘探工作量却很少，因而笔者应用所提出的勘探模型，确定该地区油田对模型的响应，以验证模型对勘探的指导作用。

4 应用实例

德兹夫尔海湾地区油藏呈不对称长轴背斜形态，北西—南东走向，目的层为裂缝性灰岩[11]。航摄地质和地表地质研究并未证明该地区存在油田，根据表 1所列标准，该地区的油田对于航摄地质和地表地质研究的响应为零，但其对重力勘探、构造测试井和地下地质研究的综合响应为80%。

由图 4可以看出，构造地质研究和测试井未能准确定位目标区，即背斜高点，测试井位位于背斜翼部。

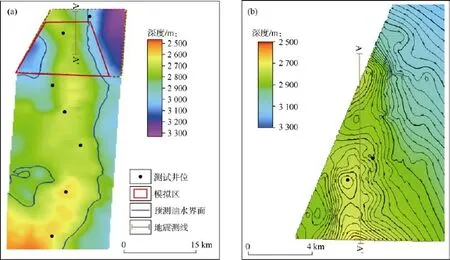
图4 目标区井位和某油田构造地质图

图 5所示为图 4中 A—Aʹ测线地震剖面，从中清晰可见背斜高点，即合适的钻井位置。说明在这些地区，采用地球物理技术勘探效果更好。然而，选择测试井井位时仅使用了孔隙度分布图（见图 6a），图 6b所示为投产后得到的净毛比（有效厚度和总厚度比值）分布图，可见 2张图差别非常大。目标油藏的总孔隙度和盖层孔隙度分布见图7，结果再次表明，目的层的高孔隙度区与盖层的低孔隙度区并不一致。目标区较好的产层应该是地震勘探所确定的层段。这充分说明，研究区油气系统并非仅受构造控制，下一步勘探中应考虑由于岩相变化而形成的地层圈闭。

图5 目标区地震剖面（剖面位置见图4）

图6 目标区平均孔隙度分布与净毛比分布图

图7 目标地层孔隙度及盖层孔隙度分布图

5 结语

文献[12]提出了未知数目非均匀目标序贯指示优选法，是迄今为止唯一设计用作测试网格钻井勘探方法有效性的研究成果，但该研究也只是做了有限的尝试，尤其是它将网格钻井期限延长到了10年，并假设市场供应不会产生价格方面的响应。

网格钻井的油藏定位成功率至少与分阶段勘探模拟相当。事实上，对于具有巨大地层圈闭含油气潜力的盆地，网格钻井定位油藏的准确性更高。但在盆地勘探的各个阶段，多阶段序列勘探方法的投资回报比网格钻井大得多，约为网格钻井总投资回报的两倍。在资本效率方面，分阶段序列勘探远比网格钻井有效。这一点证实了理论预测的结果，即由于存在更经济的方法，网格钻井并没有被用作主要的勘探策略。

概念决策模型在伊朗西南部德兹夫尔海湾的应用实例证实了模型的准确性。研究区储集层受构造要素控制，要准确确定油藏规模和目标点，应依据地震勘探方法，而非地质图和地下构造图。

[1] Attanasi E D, Drew L J. Lognormal size distribution as a consequence of economic truncation[J]. Mathematical Geology, 1985,17： 335-351.

[2] Davis J C, Harrbaugh J W. A simulation model for oil exploration in continental shelves[J]. Economics of Exploration for Energy Resources, 1981, 26： 19-50.

[3] Cozzolino J M. Measurement and projection of exploration search efficiency[R]. SPE 7456, 1979.

[4] King K R. Bayesian decision theory and computer simulation applied to multistage, sequential petroleum exploration[D]. Pennsylvania：The Pennsylvania State University, 1971.

[5] Hantschel T, Kauerauf A. Fundamentals of basin and petroleum systems modeling[M]. New York： Springer Publishing, 2009.

[6] Allen P A, Allen J R. Basin analysis： Principles and application to petroleum play assessment[M]. 3rd Edition. New Jersey： Wiley-Blackwell, 2013.

[7] Schneider F, Wolf S, Faille I, et al. A 3D basin model for hydrocarbon potential evaluation： Application to Congo offshore[J]. Oil and Gas Science and Technology, 2000, 55： 3-13.

[8] Pannell D J. Sensitivity analysis of normative economic models：Theoretical framework and practical strategies[J]. Agricultural Economics, 1997, 16(2)： 51-60.

[9] Telnaes N, Zwach C, Fladmark G. 3D basin modeling： A new tool for petroleum system analysis[R]. Calgary： 16th World Petroleum Congress, 2000.

[10] Kagawa T, Zhao B, Miyakoshi K. A case study in constructing a 3-D basin structure model corresponding to information available in the target area[R]. Vancouver： 13th World Conference on Earthquake Engineering, 2004.

[11] Müller J P, Guzofski C, Rivero C. New approaches to 3D structural restoration in fold-and-thrust belts using growth strata[R]. Calgary：AAPG Annual Meeting, 2005.

[12] Cozzolino J M. Sequential search for an unknown number of objects of nonuniform size[J]. Operational Research, 1979, 20： 293-308.