复杂滑移线场的三种理论求解方法及其应用
2013-01-15江荧彭炎荣
江荧,彭炎荣
(1.南京航空航天大学能源与动力学院,江苏 南京 210016;2.芜湖职业技术学院机械工程系,安徽 芜湖 241006;3.湘潭大学机械工程学院,湖南 湘潭 411105)
0 前言
滑移线场理论是利用理想弹塑性材料塑性变形过程中最大剪应力迹线的性质,求解塑性力学边值问题的一种严密方法。它满足塑性力学平面问题的所有控制方程和边界条件,作为经典塑性理论的重要组成部分,广泛地应用于金属塑性成型、结构塑性极限分析和土力学等工程领域[1],文献[2]和文献[3]描述了滑移线场理论在金属成型领域中的具体应用实例。利用滑移线方法模拟金属成形过程,关键在于建立准确的滑移线场。若滑移线场是由均匀场、中心场、渐开线场、对数螺线场和摆线场等构成,其建立并不困难,因为这些场中的滑移线均可用精确的解析式来描述。但对于复杂滑移线场,如,有心扇形场,其滑移线就没有准确的方程来表达,这就给求解塑性成型问题带来很大困难。而这方面的研究尚未有详细、系统的分析资料。本文将系统介绍构建复杂滑移线场的三种理论求解方法,并给出具体计算方法和解题步骤。
复杂滑移线场中的有心扇形场在求解实际问题时应用极为普遍,而且形式各异,板坯在粗糙平砧间镦粗,或者在光滑楔形模中挤压时,有心扇形场两基线圆弧半径r1和r2相等,如图1(a)和图1(b)所示,而板坯在粗糙楔形模中挤压时,两基线圆弧半径r1和r2却不相等,如图1(c)所示;板坯在粗糙平砧间镦粗时,两圆弧对应的中心张角θ和ψ相等,如图1(a)所示,在光滑或者粗糙楔形模中挤压时,两圆弧对应的中心张角θ和ψ又不相等,如图1(b)、图1(c)所示。

图1 三种复杂有心扇形滑移线场案例
根据两基线圆弧半径r1、r2和对应的中心张角θ和ψ建立有心扇形场,其数学理论属于求解双曲型偏微分方程组的第一类边值问题(黎曼问题),可以通过理论计算求解或作图方法求解。现以有心扇形场为例,系统介绍三种理论计算求解方法。考虑到图1(c)所示的非对称型(r1≠r2,θ≠ψ)扇形场的应用更为普遍,而文献中论述又较少,故本文选择非对称有心扇形场为例,其求解的基本原理和方法也可以推广应用于其他复杂形式的滑移线场。
1 数值积分法
1.1 基本原理
图2为滑移线单元网格。

图2 滑移线单元网格
基于滑移线方程来构建复杂滑移线场的数值积分法基本原理简述如下:
先将图2所示滑移线方程:
改写为差分方程的形式:

式(2)中所有下标均表示图2中的对应节点。
由汉基第一定理知:
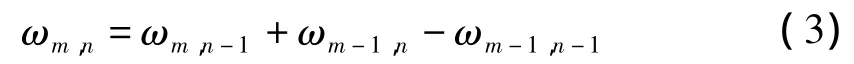
由式(2)可解得点(m,n)的坐标值:

如果已知图2中曲边矩形表示的单元网络中3个节点的ω值和坐标位置,利用式(3)和式(4)就可以求得第4个未知节点的ωm,n和坐标(x,y)值。
1.2 讨论
数值积分的特点是所用的差分方程原理简单易懂,容易掌握。且分度角△越小则网络越细,求解结果越准确[4],但计算工作量随之增加。
该方法的缺点是必须知道单元网格的3个节点,才能求得第4个节点。因此,计算只能从节点(0,0)开始,先沿基圆进行,再依次向有心扇形场内部逐点“扩散”,不能直接计算场中某指定节点(m,n)的坐标位置,也不能直接确定塑性区的边界滑移线,这在实际应用中不便。
2 解析求解法
2.1 基本原理
图3为解析计算法求解有心扇形场。
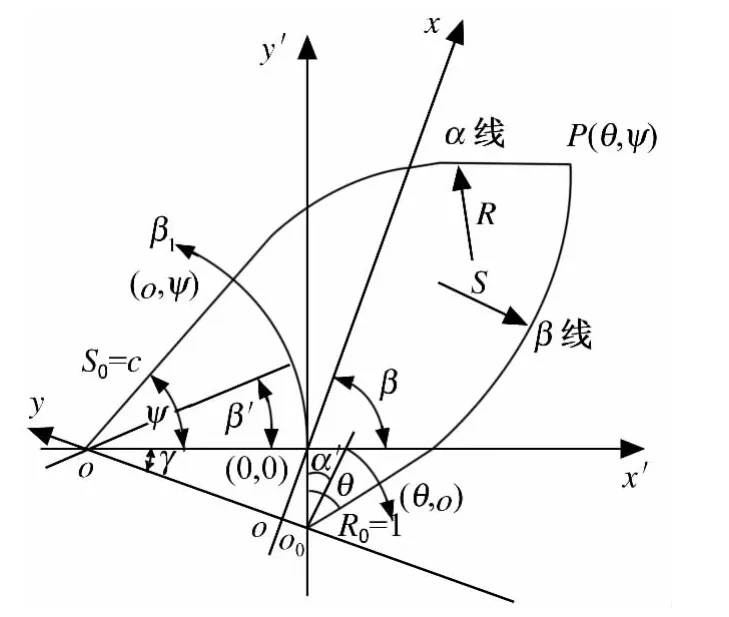
图3 解析计算法求解有心扇形场
解析求解法在一般书刊文献中都没有介绍。其基本原理是先通过解偏微分方程求得滑移线曲率半径的近似解析解,再利用曲率半径与节点位置的关系求得各节点的坐标。求解过程简述如下:
由汉基第二定理知,图3中α和β两族滑移线的曲率半径R和S之间有下述关系:

从而有:

将式(6)带入式(5),即得到一组双曲型方程:

式(7)又称为电报方程,可用纯粹的解析方法求解。如对式(7)中的第一式求解,即得到α线在节点 P(θ,ψ)处的曲率半径 R(θ,ψ)为:

式(8)中J0为零阶贝塞尔函数,角度α'和β'如图3。
R(0,0)也就是节点(0,0)处 α1基线圆弧的半径R0(考虑到α1弧线方向为顺时针走向,曲率半径规定为负值,故R(0,0)=-R0,而β1基线圆弧的半径则相反,其S(0,0)=+S0。
由汉基第二定理知,沿β1圆弧上各点的α线的曲率半径R为:

将式(9)代入式(8)积分可得:

其中,I0和I1为第一类变型贝塞尔函数。
为计算简便,在以下推导中,令式(10)的R0=1(单位长度),于是 S0=c。
现选定(x',y')直角坐标系,如图3。由微分几何原理知,图3中与张角(θ,ψ)对应的节点P的坐标可通过该点的曲率半径 R 来确定,其关系式为:

其中:
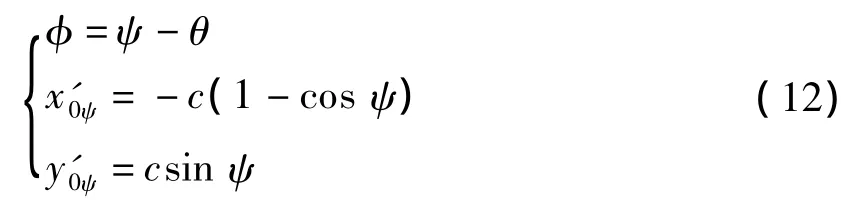
将式(10)代入式(11)进行分部积分,最后得到滑移线场中任意节点 P(θ,ψ)处的坐标,)的表达式如下:

其中:

2.2 求解方法
在具体计算有心扇形场中所有节点的坐标时,一般先将α1和β1基线圆弧按Δ微小角度等分,于是有:

将式(15)代入(14)式得:
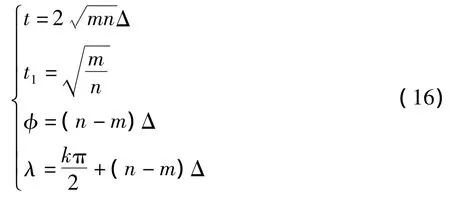
为了便于和数值积分法比较,应将图3中的(x',y')坐标进行转换,坐标转换公式如下:

2.3 讨论
因式(13)中的级数收敛性很好,故这种方法求解过程简单,获解迅速,求解精度很高。
这种方法突出的优点是不需依次逐点进行数值计算。由式(13)就可以直接求出滑移线场中与任意一组(θ,ψ)或(m,n)值对应的某节点P的坐标值(xmn,ymn),也可以直接求出塑性区的边界滑移线,而不必计算出场中整个网络的全部节点,这在求解实际问题时是非常适用的。
3 矩阵算子法
矩阵算子法是将α和β两族滑移线的曲率半径R和S用均匀收敛的双幂级数表示,级数的系数则用列向量X表示,应用矩阵算子法和叠加原理即可求解滑移线场。此法的基本原理在文献[5]和文献[6]中已有详细的论述,本文只针对有心扇形场的建立,说明其求解过程。
3.1 先求各滑移线的系数列向量X
图4中,已知基线圆弧OA的半径R0=1和圆弧OB的半径S0=c,故其系数列向量XOA和XOB分别为:

与任意一组张角(θ,ψ)对应的滑移线AP和BP的列向量分别为:

XBP和XAP与基线圆弧的列向量XOA和XOB有以下关系:
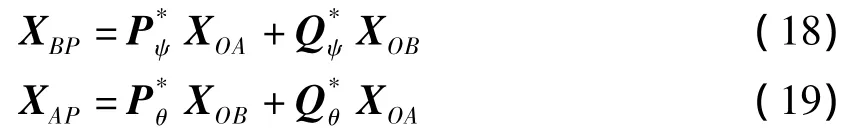
其中,P*和Q*均是矩阵算子,定义如下:

以上矩阵中的元素ψn和θn分别为:

3.2 求AP滑移线上各点(以P点为例来说明)的坐标(x',y')
先对AP线建立专用的所谓Mikhlim坐标系。这是一种转动坐标,原点为A点,而ξ和η两坐标轴分别与AP线在P点处的切线和法线平行(图4)。显然,随着P点在AP线上位置的变动,ξ轴和η轴也随之转动。P点的坐标(ξ,η)值按下式计算:
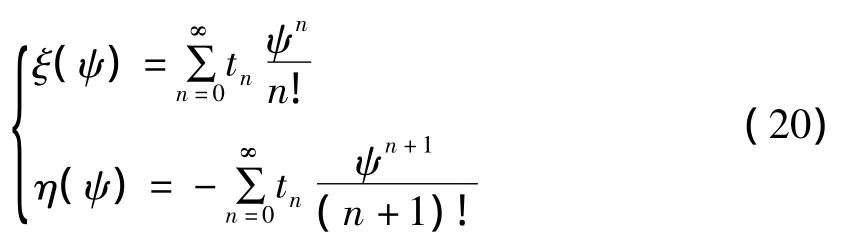
其中,tn由AP线列向量XAP的元素Sn来确定,其计算公式为:

从而求得:
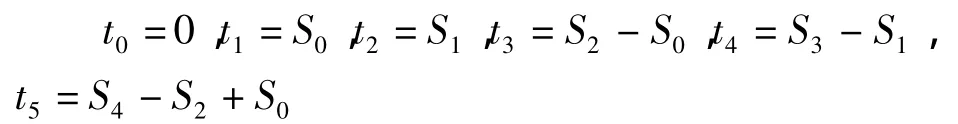
将这一系列t值代入式(20),即可求得P点的坐标(ξ,η)值。
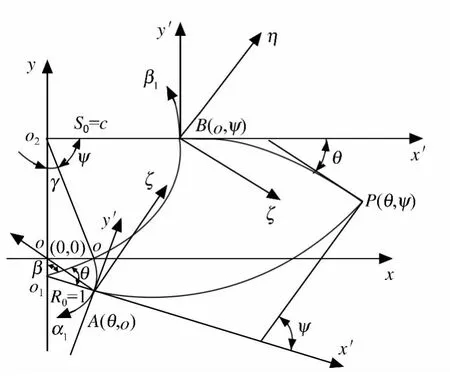
图4 矩阵算子法求解有心扇形场
再将坐标(ξ,η)换成固定坐标(x',y'),固定坐标(x',y')仍以A为原点,但以AP线在A处的切向和法向作为x'轴和y'轴的方向(图4)。将式(20)求得的(ξ,η)值代入下述坐标变换公式,即得 P 点的(x',y')值。
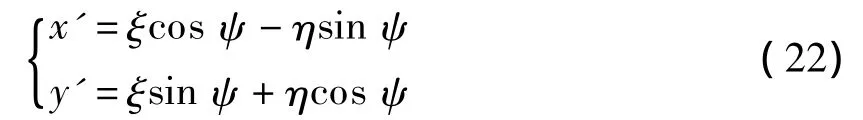
最后将专用的固定坐标(x',y')换成图4所示的统一坐标(x,y)。如,A点坐标(xA,yA)为:

AP线上任意一点P的坐标(xp,yp)为:

3.3 求BP滑移线上各点(仍以P点为例)的坐标
求解BP滑移线上各点坐标的方法同上,但须注意以下几点:
1)应以 B点为原点建立 BP线的(ξ,η)和(x',y')专用坐标系。
2)因BP线属于顺时针旋转走向,曲率半径应为负值,故对式(20)的符号应作如下修改:
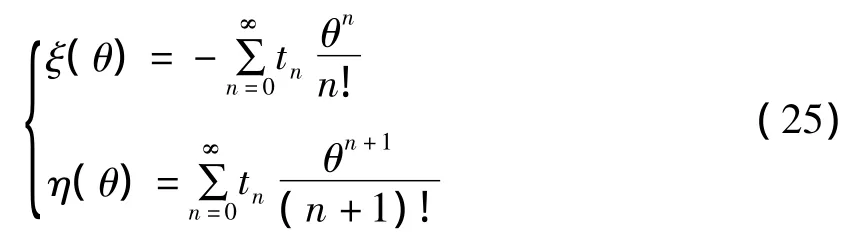
式(25)中的系数t则应由BP线列向量XBP的元素rn来确定,即:

而式(22)则应改为:

3)由式(26)求得专用固定坐标(x',y')后,应按式(27)变换成统一的坐标(x,y)。如,B点坐标为:
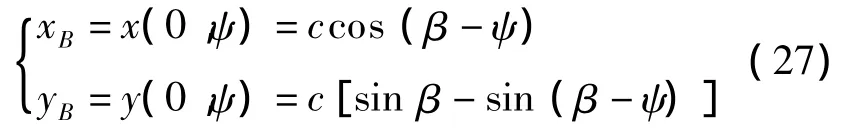
而BP线上任意一点P的坐标为:
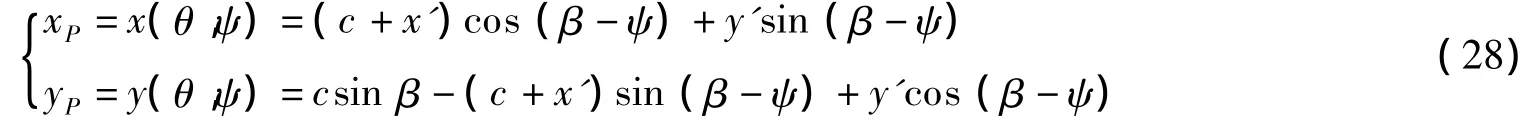
当然,由式(28)求得的结果,应与式(24)的结果一致,因为二者都是同一点P的坐标值。
3.4 节点(m,n)的坐标值
若将两基线圆弧按△微小角度等分,则只要将θ=mΔ、ψ=nΔ代入上述计算过程,由式(28)和式(24)求得的(xp,yp)值也就是节点(m,n)的坐标(xmn,ymn)值。
3.5 讨论
所有列向量X和矩阵算子P*、Q*,虽属无穷级数,但实际计算中,取6×6阶矩阵已够精确。
矩阵算子法不仅可以求解滑移线场,还可以计算滑移线场中力的分布和速度分布,特别是求解没有已知滑移线,需根据速端图或滑移线几何性质来推导的所谓间接型问题。在用滑移线方法模拟塑性成形过程时,矩阵算子法将起重要作用。
矩阵算子法求解过程看似繁琐,但若能熟悉矩阵运算方法,特别是可以将种类繁多的矩阵算子预先编好子程序以待随时调用,则方法仍然很便捷。
4 三种理论解法求解结果的比较
为了便于比较,以书刊文献中常用的对称型有心扇形场为例,并令,滑移线网络按Δ=5°等分,张角θ=ψ=135°。笔者用三种理论解法对全部节点逐点进行了计算,现仅将对称轴线(x轴)上节点坐标x用三种方法计算的结果列出,如表1所示。
由表1可见,三种方法所得结果相差极小。如果以数值积分法求解的结果为标准,则θ≤45°时,解析法求解的结果与数值积分法求解结果相比相差0.04%,矩阵算子法的求解结果与数值积分法的求解结果相比相差0.06%。θ≤90°时,解析求解法求解结果与数值积分法求解结果相比相差0.18%,矩阵算子法求解结果与数值积分法求解结果相比相差0.53%。即使θ=135°时,解析求解法的求解结果与数值积分法的求解结果相比也只差0.34%,矩阵算子法的求解结果与数值积分法的求解结果相比相差1.93%。
实际应用中,θ值一般不超过90°,因此三种理论的求解方法精度都相当高,完全满足工程应用和精细研究的要求。
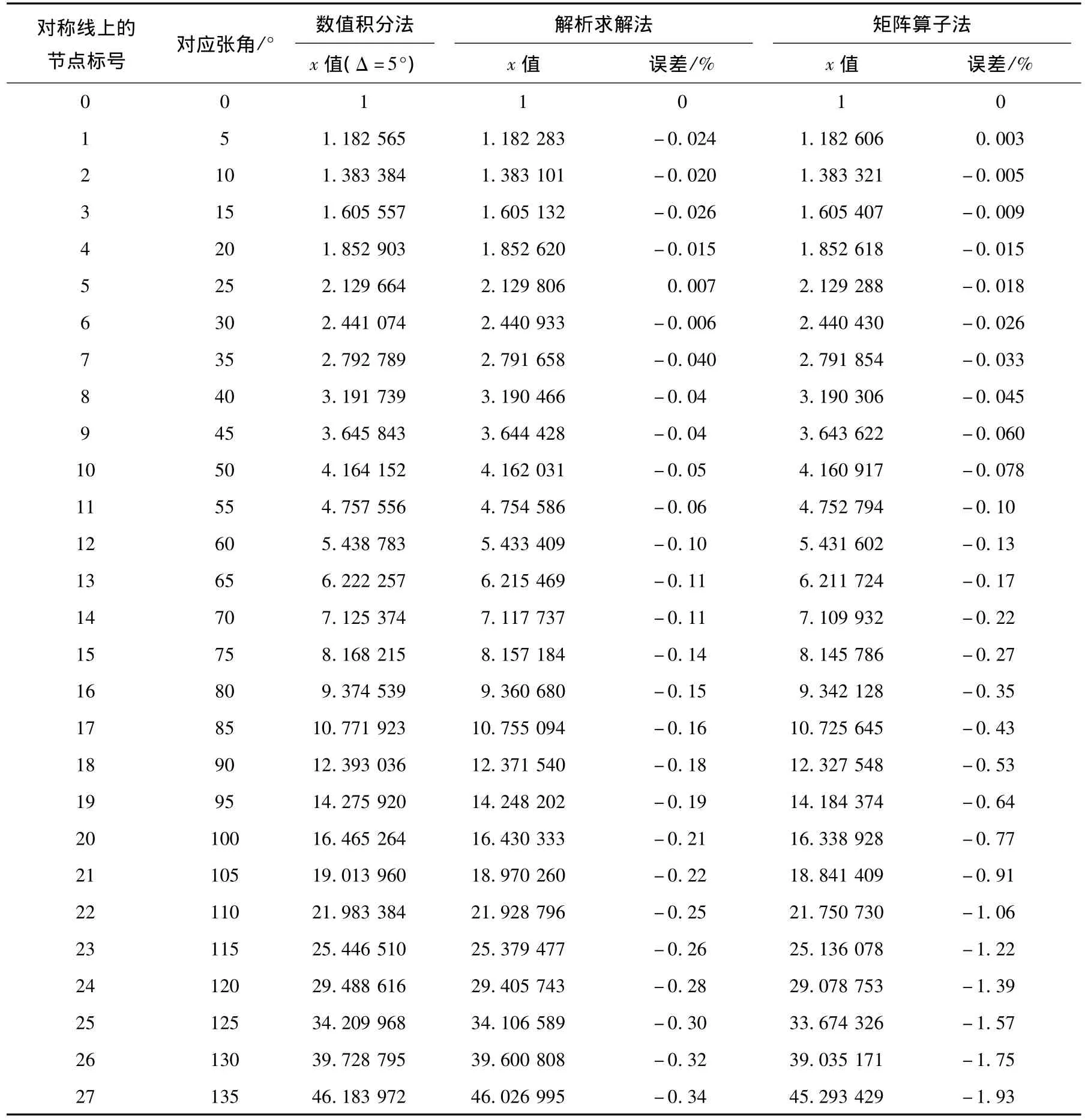
表1 有心扇形场对称线上节点坐标x用三种方法求解结果的比较
[1]曾钱帮,刘彤,马平.广义Hoek-Brown破坏准则平面应变问题的滑移线场理论[J].土木建筑与环境工程,2010,32(1):4-11.
[3]秦小琼,刘德学.杯形件反挤压变形力的滑移线场数值分析解[J].山东大学学报:工学版,2011,41(6):66-69.
[3]严志远,雷步芳,李永堂,等.基于滑移线理论计算板料弯曲变形力[J].机械工程与自动化,2011,168(5):176-178.
[4]罗中华,罗文波,彭炎荣.一种高精度有心扇形滑移线场的近似解析解[J].锻压技术,1999,24(1):43-45.
[5]Johnson W.Plane-strain Slip-line Field for Metal-deformation Processes[M].Oxford:Pergamon Press,1982.
[6]王祖唐,关廷栋,肖景容,等.金属塑性成形理论[M].北京:机械工业出版社,1989:232-240.
