用EXCEL模拟变加速运动的尝试

邓宏伟

(洪洞县第一中学 山西 临汾 041600)

变加速运动是中学物理教学中的一个难点，由于加速度的变化，导致速度非线性变化，从而使中学物理公式失去用武之地.

中学物理对此类运动的处理有两种方法：

(1)由现象寻找运动规律，如简谐运动的教学，就是通过频闪照相来研究弹簧振子的位移与时间的关系，从而得出其运动规律；

(2)倒推法，如带电微粒垂直进入磁场在洛伦兹力作用下的运动，并没有直接证明就是匀速圆周运动，而是先猜测出可能做圆周运动，再反推出匀速圆周运动的向心力恰好与所受洛伦兹力相同，从而证明微粒运动为匀速圆周运动.

以上两种方法都没能从受力直接推导出运动规律，难以使学生从心里上获得认同感，笔者在教学中尝试使用学生较熟悉的Excel软件来模拟物体在受到变力时的运动情形，获得了较好的教学效果，现将笔者的一些做法呈现出来，请同行批评指正.

1 总体思路

在中学物理中比较强调“微元”思想的渗透，在一个很小的时间间隔内，物理量可以化变为恒，物理量变化的关系图线可以化曲为直.

笔者正是利用这种思想，将物体的运动分隔为很多个小的时间段，将每个时间段内的运动看作匀变速直线运动进行处理，时间间隔越小，则所描述的运动越接近真实的运动.在数据处理时，如果用手工进行计算显然是难以实现的，而Excel则可以完成这个任务.

2 实例分析

2.1 探究弹簧振子的运动规律

如图1所示，一中间有孔的小球穿在一个光滑的细杆上，左端连接一轻质弹簧.弹簧的劲度系数为κ=100 N/m，小球质量为m=0.1 kg.现将小球由平衡位移置向右移动x=0.1 m，请问小球的位置坐标、速度随时间如何变化？

图1

2.1.1 设计思想

取释放小球时刻为计时起点，以小球平衡位置为坐标原点，向右为正方向.由受力分析可知小球的加速度

先在Excel表格中输入初状态的各物理量的值，再计算Δt时间后的各物理量(计算过程如图2所示)，如此不断循环，就可以算出各时刻的坐标、速度、加速度.

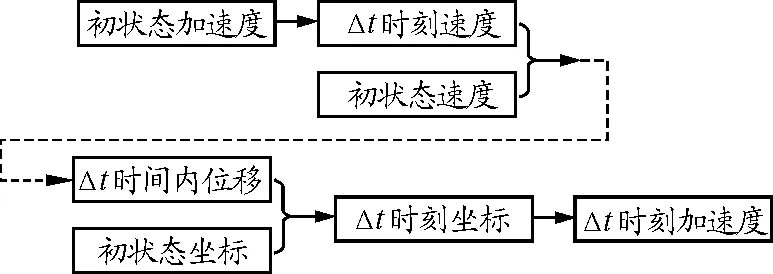
图2 计算过程框图

2.1.2 操作步骤

(1)在Excel表格的第1行输入各已知量.

在A1，C1，E1，G1单元格分别输入文字“劲度系数κ”、“质量m”、“初位置x0”、“时间间隔Δt”；在B1，D1，F1，H1单元格输相对应物理量的数值，以备后面的计算使用.

(2)在第2行写上各变量名(在A2,B2,C2,D2单元格分别输入t,x,a,v).

(3)第3行输入零时刻(初状态)的数据.

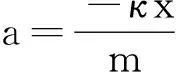
(4)第4行输入经过Δt时间后各变量的表达式.

1)算出该时刻的速度：在“D4”单元格输入该时刻的速度表达式v=v0+aΔt，其中v0,a为上一时刻的速度、加速度，Δt为提前设置的值(即H1单元格数值)，因此在单元格输入“=D3+C3*$H$1”.

2)算出该时刻的位置坐标：在“B4”单元格输入公式

(输入“=B3+(D3+D4)*$H$1/2”).

3)算出该时刻的加速度：在“C4”单元格输入该时刻的加速度表达式

(在该单元格输入“=-1*$B$1*B4/$D$1”).

(5)选择第4行，出现小箭头后向下填充即可计算出各时刻的相应物理量.

(6)选中x,t两行数据，点插入→图表→x,y散点图→光滑曲线连接，并设置数据点格式为“无”，即可作出该运动的x-t图像；同理，可作出v-t,a-t图像.

2.1.3 描绘结果

作出图线如图3所示(Δt=0.000 2 s).

将所描绘出的图线与正弦图像进行比对，可以得出结论：弹簧振子的位移、速度、加速度等物理量均按正弦规律(初相位不一定是零)变化，这样的运动叫做简谐运动.

图3

2.1.4 拓展分析

(1)改变表格中的κ,m值(只需改变“B1”,“D1”两单元格的数字)，可以研究弹簧振子的周期T与κ,m的关系.

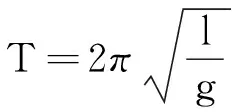
那么,在偏转角度较大时周期为多少呢？这个问题也可以用上述的方法来分析，并能得出其周期与最大偏转角的关系.

2.2 探究带电微粒垂直进入磁场仅在洛伦兹力作用下的运动规律

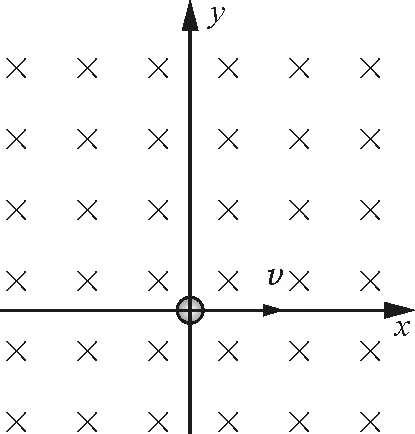
图4

如图4所示，平面内存在垂直纸面向内的匀强磁场，磁感应强度B=1 T，一带电小球(质量为m=0.016 kg ，电荷量为q=0.001 6 C)以v0=10 m/s的速度沿着x轴方向从原点处进入磁场，试分析小球将做什么运动(忽略小球的重力)？

2.2.1 设计思想

将带电小球的位移、速度、加速度、洛伦兹力正交分解.水平速度产生竖直方向的洛伦兹力，而竖直速度产生水平方向洛伦兹力，因此,由某一时刻的水平速度和竖直速度可算出该时刻在竖直方向和水平方向所受的洛伦兹力，从而求出该时刻的加速度，再由该时刻的加速度求出下一时刻的速度，如此循环，便可求出各时刻的速度及加速度，再由匀变速直线运动的规律求出各时刻的横、纵坐标值，示意图如图5所示.

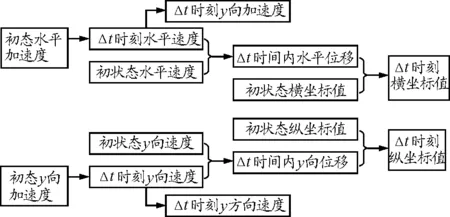
图5 设计思想示意图

2.2.2 操作步骤

(1)在Excel表格的第1行输入各已知量.

在A1，C1，E1，G1单元格分别输入文字“磁感应强度B”、“质量m”、“电荷量q”、“时间间隔Δt”；在B1，D1，F1，H1单元格输入对应物理量的数值，以备后面的计算使用.

(2)在第2行写上各变量名.

(3)第3行输入零时刻(初状态)的数据.

在“D3”单元格输入水平初速度“10”，在“C3”单元格输入公式,计算出此时的竖直方向加速度

(在C3单元格中输入“=$F$1*D3*$B$1/$D

$1”)，其他物理量均为零.

(4)第4行输入经过Δt时间后各变量的表达式.

1)算出该时刻的速度：在“D4”单元格输入该时刻的水平速度表达式

vx=vx0+axΔt

(在该单元格输入“=D3+B3*$H$1”).

同理，在“E4”单元格输入该时刻的y方向速度表达式

vy=vy0+ayΔt

(在该单元格输入“= E3+C3*$H$1”).

2)算出该时刻的加速度：

在“B4”单元格输入该时刻水平方向加速度表达式

(在该单元格输入“=-1*$F$1*E4*$B$1/

$D$1”).

同理，在“C4”单元格输入竖直方向加速度表达式

(在该单元格输入“=$F$1*D4*$B$1/$D$1”).

3)算出该时刻的坐标值：在“F4”单元格输入横坐标公式

(输入“=F3+(D4+D3)*$H$1/2”)，“G4”单元格输入纵坐标公式

(输入“=G3+(E4+E3)*$H$1/2”).

(5)选择第4行，出现小箭头后向下填充即可计算出各时刻的相应物理量.

(6)分别选择选中x,y两行数据，点插入→图表→x,y散点图→光滑曲线连接，并设置数据点格式为“无”，即可作出带电微粒的运动轨迹.同理，可作出vx-t,vy-t等图像.

2.2.3 描绘结果

作出图线如图6所示(Δt=0.033 s).

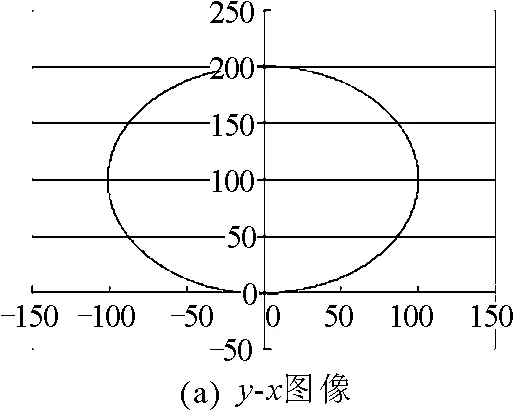
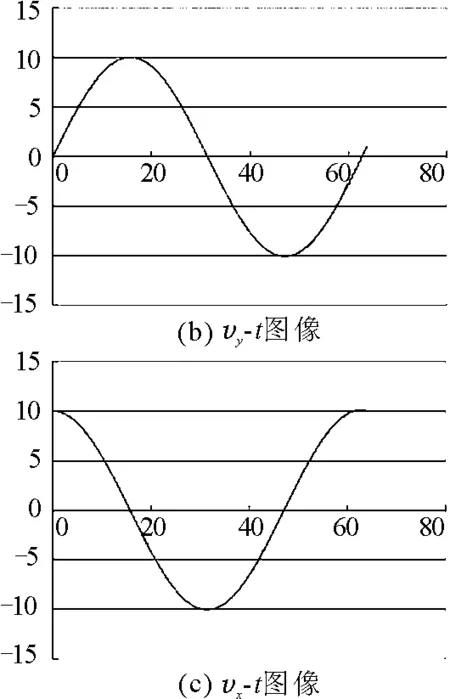
图6

通过以上分析，学生明白了在洛伦兹力作用下物体的运动轨迹是一个圆，说明物体确实做圆周运动.进一步研究可以验证圆周运动的半径公式为

周期公式为

并可通过vx,vy随时间t的变化规律对圆周运动进行更深入地理解.

2.3 探究带电小球在复合场中的运动规律

如图7所示，在足够大的范围内存在竖直向下的匀强电场(E=1 N/C)和垂直纸面向内的匀强磁场(B=3 T)，将一质量为m=0.01 kg，电荷量为q=0.1 C的带电小球，在电磁场中由静止释放，问小球做什么运动(重力加速度g=10 m/s2)？

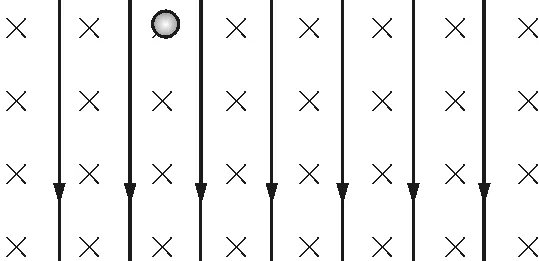
图7

2.3.1 设计思想

与情境2相同，只是竖直方向受到电场力和重力作用，因而，加速度发生变化.

2.3.2 具体操作

(1)在Excel表格的第1行输入各已知量名称及数值.

在A1，C1，E1，G1,I1单元格分别输入文字“电场强度E”、“磁感应强度B”、“质量m”、“电荷量q”、“时间间隔Δt”；在B1，D1，F1，H1，J1单元格输入对应物理量的数值，以备后面的计算使用.

(2)在第2行写上各变量名.

在A2，B1，C1，D1，E1，F1，G1单元格分别输入文字“t”、“ax”、“ay”、“vx”、“vy”、“x”、“y”.

(3)第3行输入零时刻(初状态)的数据，并计算出此时的竖直方向加速度

(在C3单元格中输入“20”)，其他物理量均为零.

(4)第4行输入经过Δt时间后各变量的表达式.

1)算出该时刻的速度：在“D4”单元格输入该时刻的水平速度表达式

vx=vx0+axΔt

(在该单元格输入“=D3+B3*$J$1”)

同理，在“E4”单元格输入该时刻的竖直速度表达式

vy=vy0+ayΔt

(在该单元格输入“= E3+C3*$J$1”).

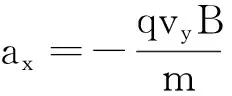
(在该单元格输入“=-1*$H$1*E4*$D$1/

$F$1”).

同理，在“C4”单元格输入该时刻的竖直加速度表达式

(在该单元格输入“=($H$1*D4*$D$1-$H$1*$B$1)/$F$1-10”).

3)算出该时刻的坐标值：在“F4”单元格输入横坐标公式

(输入“=F3+(D4+D3)*$J$1/2”)，在“G4”单元格输入纵坐标公式

(输入“=G3+(E4+E3)*$J$1/2”).

(5)选择第4行，出现小箭头后向下填充即可计算出各时刻的相应物理量.

(6)选中x,y两行数据，采用与情境2相同的方法做出带电微粒的运动轨迹.

2.3.3 描绘结果

时间间隔不同，则所获得的图线不同，图8分别为时间间隔取0.01 s，0.002 s，0.000 3 s时的图线.由图8可看出，时间间隔较大时，计算结果误差较大，时间间隔取得越小，则描绘的图像越精确，可以想像，当时间间隔取得更小时，所画图线可以更接近实际运动轨迹.

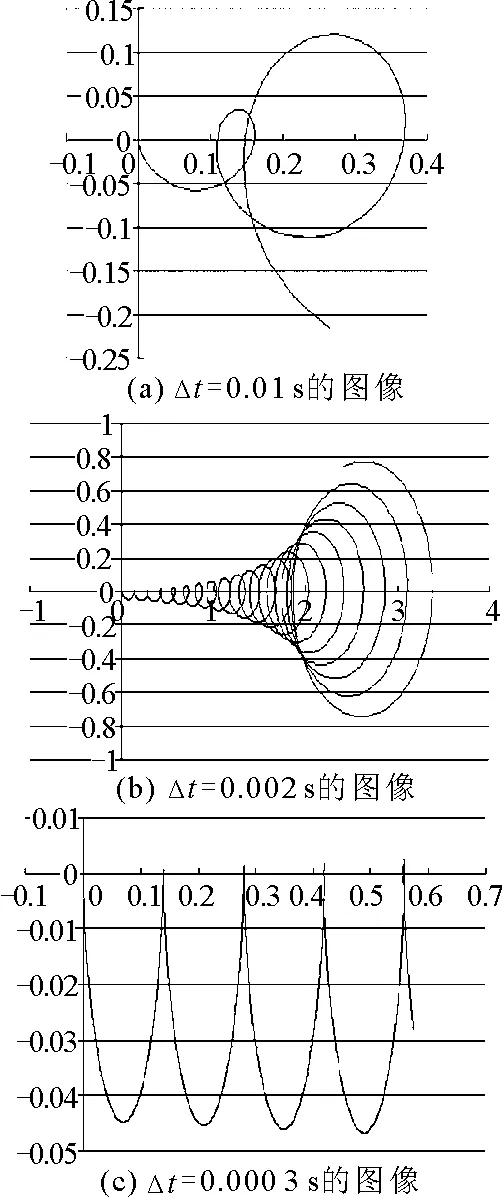
图8 不同时间间隔带电小球在磁场中的运动轨迹

2.3.4 对结果的检验

由运动的合成和分解方法，将初速度(v初=0)分解为向左和向右的两个速度，设两速度大小为v0.向右的分运动应使洛伦兹力与重力、电场力平衡，从而使物体做匀速直线运动，即

qv0B=qE+mg

向左的分运动则使小球做匀速圆周运动

由以上各式代入数据解得

则小球向下运动的最大位移为

y=2ry≈0.44 m

一个周期内小球向右运动的距离

x=v0Tx≈0.14 m

上述结果与Excel(Δt=0.003 s时)所绘出的图像完全吻合，说明本文所用方法能够比较准确的描述出小球的运动，是完全可行的.

3 该方法的应用范围及教育意义

该方法适用于中学阶段所遇到的很多变加速运动的处理过程，也可以适用于电学中的一些问题，如电容器放电时的电流的模拟等，相信通过教师的创造性工作，可以使这种模拟的思想适用于更广的范围.这种方法教学有以下几方面的教育意义.

(1)使学生对“微元法”处理物理问题有了更深入的理解，明确在时间间隔很小的情况下，用“微元法”可以很好地模拟实际情形.

(2)从学生比较熟悉的物理规律、电脑软件、物理方法出发，得出结论，获得了学生的心理认同感，使学生更容易接受知识.

(3)用计算机模拟的方法推演实际情形是一种应用很广的方法，比如在设计好一种飞机后一般要进行大量计算机模拟飞行来积累数据，验证其可行性然后再进行制造.通过本文所用的方法可以给学生渗透这样一种方法，以填补中学物理教育的一项空白.

(4)可以培养学生积极思考的思维品质，知道有时用简单的工具也可以完成复杂的任务，同时可以培养学生的创造性思维能力.