电磁感应电路中功能关系的辨析
2013-01-11程方勇
程方勇
(武汉市新洲一中 湖北 武汉 430410)
电磁感应中的功能关系是高中物理里面非常难以理解的一部分内容.特别是当里面含有电动机模型时,能量转化过程很复杂,这里面有其他能转化成电能,也有电能转化成内能和机械能等其他能,理清能量转化的过程很重要.我们知道,功是能量转化的量度,每种能的转化必定要通过某种功去实现.所以,当我们无法辨别能量的转化方向时,可以借助功去分析它.在电磁感应现象中,导体棒或者线圈克服安培力做功是量度其他能转化为电能的,往往充当发电机,而当安培力对它们做正功时,则往往是消耗电能,充当电动机.
下面,笔者通过教学过程中学生极易错的具体例题来辨析其中的功能转化关系,与同行们一起探讨.
1 双棒问题中的功能关系
【例1】(2008年2月武汉市调考)如图1所示,间距为l,电阻不计的两根平行金属导轨MN,PQ(足够长)被固定在同一水平面内,质量均为m,电阻均为R的两根相同导体棒a,b垂直于导轨放在导轨上,一根轻绳绕过定滑轮后沿两金属导轨的中线与a棒连接,其下端悬挂一个质量为M的物体C,整个装置放在方向竖直向上、磁感应强度大小为B的匀强磁场中.开始时,使a,b,C都处于静止状态,现释放C,经过时间t,C的速度为v1,b的速度为v2.不计一切摩擦,两棒始终与导轨接触良好,重力加速度为g.求:
(1)t时刻C的加速度值;
(2)t时刻a,b与导轨所组成的闭合回路消耗的总电功率.
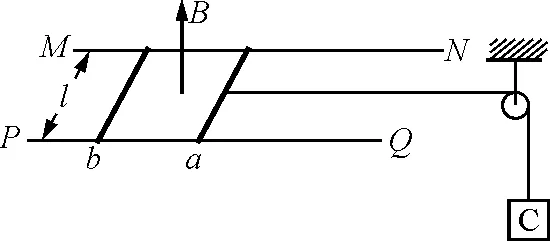
图1
解析:此题是一道力、电综合题,比较而言,力学问题不算太难.电路分析与功能分析难度较大,是此题考查的重点,且两者相互关联.第一问解答如下.
根据法拉第电磁感应定律,t时刻回路的感应电动势
(1)
回路中感应电流
(2)
以a为研究对象,根据牛顿第二定律
T-BIl=ma
(3)
以C为研究对象,根据牛顿第二定律
Mg-T=Ma
(4)
联立式(1)~(4)解得
第二问求的电路总功率,是否就是热功率,即是否P热=I2R,即
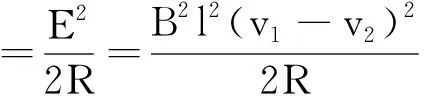
我们知道,只有是纯电阻电路时,电功率等于热功率.考查这个系统的能量转化过程如图2所示.

图2 双棒系统能量转化过程
不难发现,a棒是克服安培力做功,是产生电能的,它是发电机,而b棒是安培力做正功,是消耗电能的,它是电动机.即由两棒及导轨构成的回路并不是纯电阻电路,而是含电动机电路. 那么,电能就不是全部转化为内能,还应该加上机械能即b棒增加的动能,这样,第二问就产生了第一种解法.
解法1:闭合回路消耗的热功率
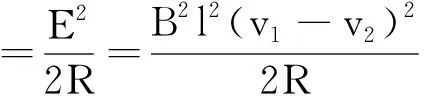
b棒的机械功率为

故闭合回路消耗的总电功率

这种解法带来了一个新问题,那就是在第一问中计算电流的方程组(1)、(2)是否正确?需要说明的是,法拉第电磁感应定律只是从数学角度给出了全电路的电动势,并未完全反映现象中全部的物理本质.实际上,本题中的感应电动势应该由电源电动势即a棒的电动势和b棒产生的反电动势组成,即
E=Ea-Eb
认清了这个问题,就给本题带来了第二种解法.
解法2:a棒等效为发电机,b棒等效为电动机.
a棒的感应电动势
Ea=Blv1
(5)
闭合回路消耗的总电功率
P=IEa
(6)
联立式(1)、(2)、(5)、(6)解得
根据功能关系,本题还有第三种解法.单位时间内,通过a棒克服安培力做功,把C物体的一部分重力势能转化为闭合回路的电能,而闭合回路电能的一部分以焦耳热的形式消耗掉,另一部分则转化为b棒的动能,所以,t时刻闭合回路的电功率等于a棒克服安培力做功的功率,即
2 磁场自身运动中的功能转换问题
【例2】如图3所示,两平行长直金属导轨置于竖直平面内,间距为L,导轨上端有阻值为R的电阻,质量为m的导体棒垂直跨放在导轨上,并搁在支架上,导轨和导体棒电阻不计,接触良好,且无摩擦.在导轨平面内有一矩形区域的匀强磁场,方向垂直于纸面向里,磁感应强度为B.开始时导体棒静止,当磁场以速度v匀速向上运动时,导体棒也随之开始运动,并很快达到恒定的速度,此时,导体棒仍处在磁场区域内.试求:
(1)导体棒的恒定速度;
(2)导体棒以恒定速度运动时,电路中消耗的电功率.

图3
解析:此题属于单棒切割磁感线,但磁场与导体棒都有运动,设棒速为v′,则由法拉第电磁感应定律得
E=BL(v-v′)
则导体棒受安培力
导体棒受力平衡有
mg=F安
联立得

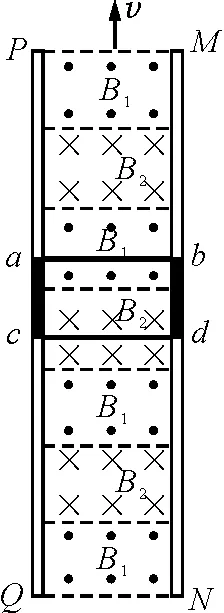
图4
【例3】随着越来越高的摩天大楼在各地的落成,至今普遍使用的钢索悬挂式电梯已经渐渐地不适用了.这是因为钢索的长度随着楼层的增高而相应增加,这样钢索会由于承受不了自身的重量,还没有挂电梯就会被扯断.为此,科学技术人员正在研究用磁动力来解决这个问题.如图4所示就是一种磁动力电梯的模拟机,即在竖直平面上有两根很长的平行竖直轨道,轨道间有垂直轨道平面的匀强磁场B1和B2,且B1和B2的方向相反,大小相等,即B1=B2=1 T,两磁场始终竖直向上做匀速运动.电梯轿厢固定在如图4所示的一个用超导材料制成的金属框abcd内(电梯轿厢在图中未画出),并且与之绝缘.电梯载人时的总质量为5×103kg,所受摩擦力f=500 N,金属框垂直轨道的边长Lcd=2 m,两磁场的宽度均与金属框的边长Lac相同,金属框整个回路的电阻R=9.5×10-4Ω,假如,设计要求电梯以v1=10 m/s的速度向上匀速运动,问:
(1)磁场向上运动速度v0应该为多大?
(2)在电梯向上做匀速运动时,为维持它的运动,磁场提供功率是多少?
解析:(1)当电梯向上匀速运动时,金属框中感应电流大小为
(7)
金属框所受安培力
F=2B1ILcd
(8)
安培力大小与重力和摩擦力之和相等,所以
F=mg+f
(9)
由式(7)~(9)求得
v0=13 m/s
(2)磁场克服安培力做功,输出能量转化为电能,分为两部分,一部分在闭合电路中由电流经电阻做功转变为金属框的内能,另一部分通过安培力对线框做正功,即克服电梯的重力和阻力做功,转化为电梯的势能和摩擦内能.当电梯向上做匀速运动时,金属框中感应电流由式(7)得
I=1.26×104A
金属框中的焦耳热功率为
P1=I2R
代入数据得
P1=1.51×105W
(10)
而电梯的有用功率
P2=mgv1
代入数据得
P2=5×105W
(11)
阻力的功率
P3=fv1
代入数据得
P3=5×103W
(12)
磁场提供总功率
P总=P1+P2+P3
代入数据得
P总=5.56×105W
结论验证:当电梯匀速运动时,电梯所受阻力或安培力是重力与摩擦力的合力
F=mg+f
代入数据得
F=5.05×104N
安培力与磁场速度的乘积
P=Fv0
代入数据得
P=5.56×105W
即安培力与磁场速度的乘积是磁场提供的电功率.通过计算进一步证明上面结论正确.
通过以上分析,我们发现电能的转化是通过克服安培力做功才实现的,对象可以是导体棒、线圈或者磁场,它们是发电机.而消耗电能是闭合电路里面通过电流做功去实现.用电器不同,电能转化的方向不同.纯电阻电路的电能全部转化为内能,而当有安培力对导体棒或者线框做正功时,就有了电动机,尽管也切割磁感线,但它并不产生电能而是消耗电能.我们注意到,新课标的教材与大纲版教材在本章有很大区别,其中,在这一部份,新课标教材《物理·选修3-2》引入了反电动势的概念,值得我们重视.另外,也可把这一部份与恒定电流里面的含电动机电路作对比分析,能帮助学生进行理解.
