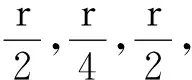电阻网络Y—△变换恒等式

吴好

(镇江中学 江苏 镇江 212017)

在某些复杂的电路中往往会遇到电阻的Y型接法[如图1(a)]或△型接法[如图1(b)]．有时需要将Y型联接代换成等效的△型联接，或将△型联接代换成等效的Y型联接，从而达到对电路进行简化计算的目的．两种变换的关系不太容易记住，如果在记忆方法上有所突破，就会对学生准确运用规律处理实际问题带来方便．

本文在对电路元件为电阻的情形进行讨论的基础上，提出了“Y—△变换恒等式”，为方便记忆给出口诀，并通过例题说明了Y—△的变换方法．

1 两种类型网络的变换式

(1)将Y型网络变换成△型网络的变换式

(1)

(2)

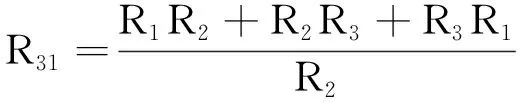
(3)

(2)将△型网络变换成Y型网络的变换式

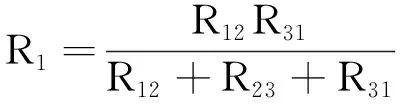
(4)

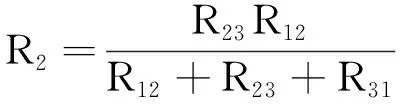
(5)

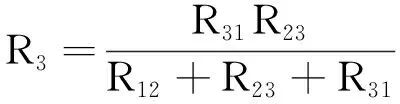
(6)

2 两种类型网络的变换式的证明过程

等效代换要求Y型联接三个端点间的电压U12,U23,U31以及流进三个端点的电流I1,I2,I3与△型联接对应部分完全相同．本文假设流进三个端点的电流方向以及△型联接每个电阻的电流方向如图1所示．

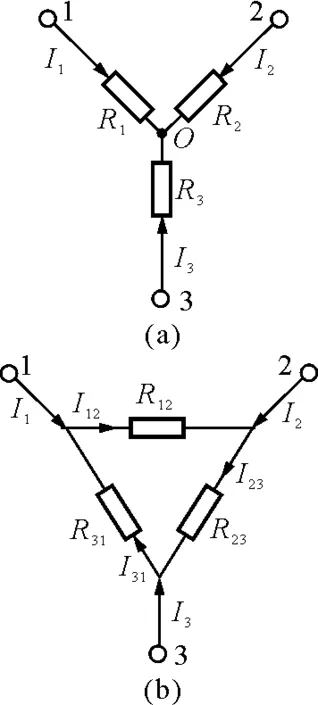
图1

2．1 证明方法一

根据Y型网络有

I1R1-I2R2=U12

I2R2-I3R3=U23

I1+I2+I3=0

可以得到

(7)

根据△型网络可以得出

I2+I12=I23

联立可以得到

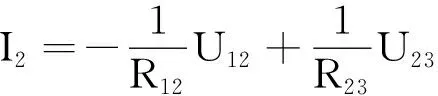
(8)

由(7)、(8)两式得

U12与U23取不同数值时上式恒成立的条件是，U12与U23的系数均为零.根据U12与U23的系数为零容易得到(1)、(2)两式;按照类似的方法可以得到式(3)．

将式(1)、(2)、(3)相加并化简得到

将式(1)和(3)、式(1)和(2)、式(2)和(3)分别代入上式可以得到式(4)、(5)、(6)．

2．2 证明方法二

根据Y型网络与△型网络“1，2”间、“2，3”间、“3，1”间的电阻对应相等得到

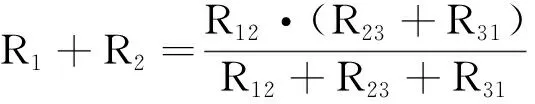
(9)

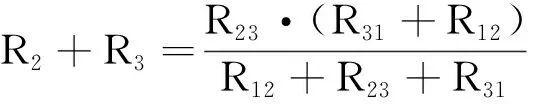
(10)

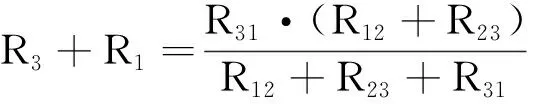
(11)

将(9)、(10)、(11)三式相加得

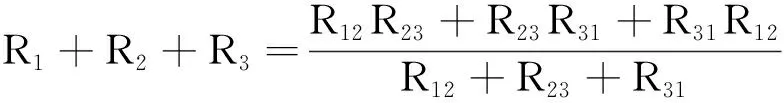
(12)

分别联立式(10)和(12)、式(11)和(12)、式(9)和(12)得到式(4)、(5)、(6),将式(4)、(5)、(6)两两相乘再相加并化简得到

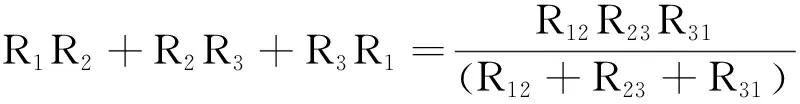
(13)

再将式(4)、(5)、(6)分别代入式(13)容易得到式(1)、(2)、(3)．

3 Y—△变换恒等式

利用式(1)、(2)、(3)、(13)，或式(4)、(5)、(6)、(13)可以得到“Y—△变换恒等式”

R1R2+R2R3+R3R1≡

(14)

利用式(14)的左边关系式等于右边关系式得到式(1)～(3), 利用式(14)的中间关系式等于右边关系式得到式(4)～(6).

“Y—△变换恒等式”的记忆口诀是：“星型电阻积之和、角型电阻积比和、星角相对积全等”．

很显然，利用“Y—△变换恒等式”并结合记忆口诀很容易推出式(1)～(6)，并便于记忆.

4 例题

【例1】如图2(a)所示，一个立方体原来用12根相同的电阻丝构成立方体框架，每根电阻丝的电阻均为r，现将其中一根拆去，求A，B两点间的电阻．

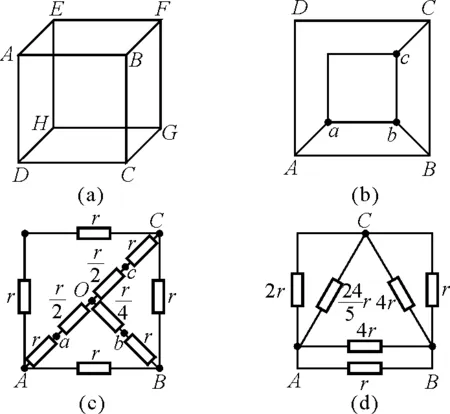
图2