牛顿迭代法在物理竞赛中的应用

许文龙 戴凤国

(浙江瑞安中学 浙江 温州 325200)

2012年全国第29届物理竞赛复赛结束后，一些学生议论说：“其中一道考题虽已列出式子，但却是一元高次方程，发现无法进行因式分解，实在没法求解出结果．”物理竞赛题不同于普通考试的“凑数题”，题中所给数据往往来自更切合客观规律的实际观察或实验结果，所遵循的数学形式通常是一些高次方程，且无法因式分解．三次方程求根公式已非常复杂了，没有多少人能记住，而四次及以上，根据阿贝尔定理，没有一般的由方程的系数经有限次四则运算和开方运算的求根方法．解决这类高次方程只能用数值分析，而牛顿迭代法就是数值分析中最常用的，令人兴奋的是牛顿迭代法能在普通计算器中实现求解高次一元方程，而物理竞赛恰恰可以使用普通计算器．

1 牛顿迭代法原理

设f(x)在[a，b]上连续，f′(x)也连续，且f′(x)≠0,f″(x)≠0，f(a)f(b)<0，(设f(a)<0，f(b)>0)，过点[a，f(a)]或点[b，f(b)]作曲线的切线，它与x轴的交点为

如图1所示，其迭代式为

并取初始值

图1

2 牛顿迭代法应用举例

第29届物理竞赛复赛试题第2大题第2问，由天体运行规律列出方程

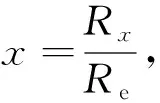
f(x)=x5-x3-583.2x+583.2=0

一阶导函数f′(x)=5x4-3x2-583.2，迭代法解此方程步骤如下：

给f(x)一个初值x0，算得

再将x1代入算得

依次算得x1，x2，x3，…直至x稳定在xn这个值，这个稳定的值xn就是方程的一个根.

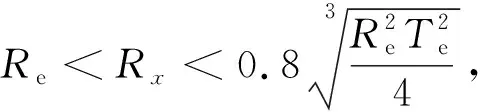
学生一般使用的是卡西欧计算器(CASIO-fx-82ES)，这种计算器普及率很高，就笔者所在学校几乎是人手一个．此计算器右下角等号旁边有一个Ans键支持迭代运算，如图2所示．

图2

我们所要做的就是给Ans赋初值，并将

输入计算器．操作步骤如下：

(1)在计算器中输入初值5，然后按一下“=”键，初值就会赋给Ans键.

(2)再输入Ans-(Ans5-Ans3-583.2Ans+583.2)÷(5Ans4-3Ans2-583.2).

(3)输入完毕，按等号键“=”，出现一个值，再按一次“=”，出现的值变了吧．继续按个3,4次．前几个值会相差很大，到最后结果会逐渐稳定，直到稳定在4.682 062 186.

迭代中也可以换不同的初值试试，而且不需要再次输入那一串长式子，CASIO计算器有存储功能，给Ans换个值，按“向上键”调出之前的式子，接着按“=”号就可以了，非常方便．