利用功能关系处理“连接体”问题探究
2013-01-11潘铁鹏
潘铁鹏
(江苏省沛县中学 江苏 徐州 221600)
“连接体”问题在高中物理中随处可见,常见的有“轻杆连接体”“轻绳连接体”“轻弹簧连接体”及“软绳、软链、液体类”等.以这些“模型”为基础设计的题目历来是考查的重点和难点,在历届高考题中屡见不鲜,且难度较大.利用功能关系如何处理此类问题?处理过程中又有哪些事项需要注意?笔者就此问题通过实例探究,归纳了题型特点,强调了注意事项,总结了解题的一般规律和方法.
1 轻杆连接体
1.1 绕某一固定轴转动
题型特点:通过轻杆相连的物体在绕固定转轴转动时,物体的角速度相等.
【例1】一质量不计的直角三角形支架两端分别连接质量为m和2m的小球A和B,支架两直角边长分别为2L和L,支架可绕固定轴O在竖直平面内无摩擦转动,如图1(a)所示,开始时OA边处于水平位置,由静止释放,则
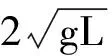
B.A球速度最大时,两小球的总重力势能最小
C.A球速度最大时,两直角边与竖直方向的夹角为45°
D.A,B两球最大速度之比为2∶1
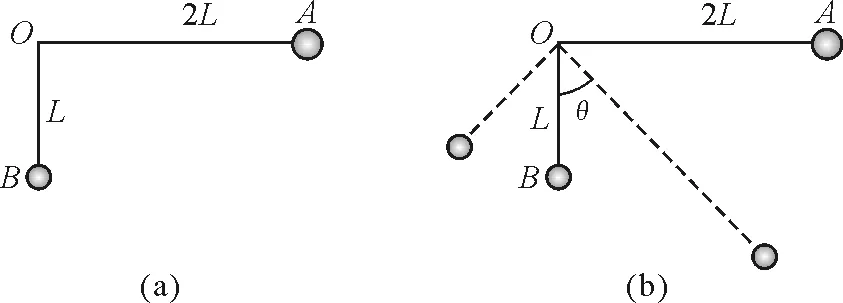
图1
解析:设轻杆与竖直方向成θ角时,如图1(b),系统动能最大,由机械能守恒可得
mg2Lcosθ-2mgL(1-sinθ)=
(1)
vA=2vB
(2)
由式(1)、(2)得
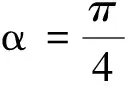
由以上分析可知本题答案为选项B,C,D.
点评:此类问题一般根据机械能守恒定律或动能定理处理,处理过程中要注意因轻杆转动造成的“连接物体”间的角速度相等这一牵连关系.
1.2 无固定转轴 沿某一支撑物滑动
题型特点:连接体做各点角速度、速度都不同的一般性滑动.
【例2】一长为l的轻杆,两端分别固定有质量为m的小球A和B,竖直立在墙壁处,已知竖直墙壁与水平面均光滑,受一微小扰动后,轻杆由静止开始下滑,当杆与水平面成θ角时,如图2所示,求此时A球的速度大小.
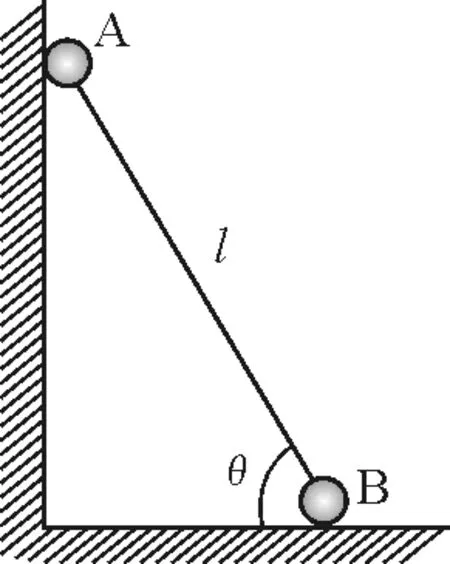
图2
(3)
由两球沿杆方向速度相同有
vAsinθ=vBcosθ
(4)
由式(3)、(4)可得
点评:此种情况往往要在利用功能关系的基础上,对被连接物体的速度进行分解,利用物体沿杆的速度相等来分析不同物体间速度的关系.
2 轻绳连接体
2.1 利用轻绳约束物体运动形式
题型特点:物体的运动受绳的约束,只能沿着特定的轨迹运动,有时由于绳瞬间的“绷紧”还会造成机械能的损失.
【例3】如图3所示,一根长为l的轻绳,一端固定在O点,另一端拴一个质量为m的小球.用外力把小球提到图示位置,使绳伸直,与水平面成θ=30°角.从静止释放小球,求小球通过O点正下方C时绳中的拉力大小.
解析:以小球为研究对象,其运动过程可分为三个阶段,如图4所示.
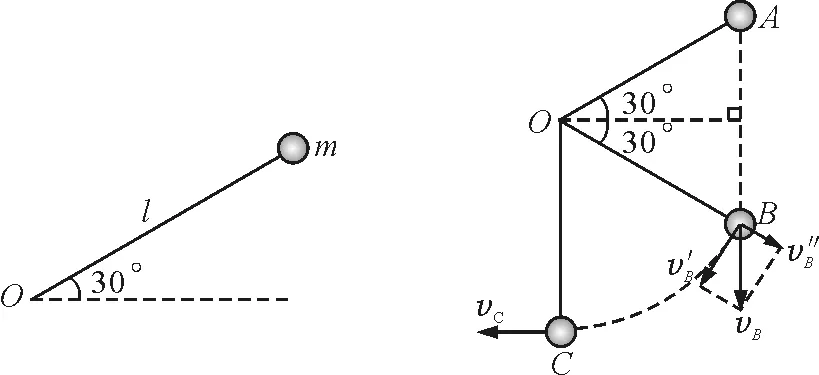
图3 图4
(1)从A点到B点的自由落体运动
但我们也应当清醒地意识到,与发达国家相比,在绿色农药的新结构、新品种、环境友好新剂型的研究开发方面,与国际先进水平仍有较大的差距。同时,行业长期以来的粗放式发展,安全环保事故频发,处于产业链低端,且大宗产品产能过剩,使得部分地方与民众对农药生产持有强烈的抵触情绪和反对态度,使行业发展蒙上阴影。但是,目前不加区别的一刀切式强令停工停产,迫使农药制造有加速向印度等国转移的趋势。一旦失去了包括农药工业在内的中国制造业优势,可能再也回不来了。中国改革开放以来巨大的进步和发展证明:“化工及农药生产解决了我们的衣食住行,改善并将继续改善我们美好的生活”。
据机械能守恒定律有
(5)
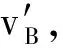
(6)
(3)小球由B点到C点的曲线运动,机械能守恒,有
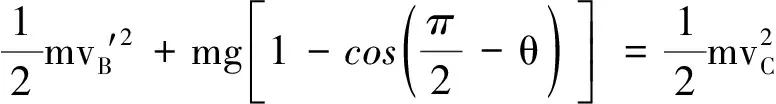
(7)
在C点由牛顿第二定律得
(8)
联立式(5)~(8)解得
点评:处理这种问题时,要注意系统的机械能是否守恒,是整个过程守恒,还是某一过程守恒.“突变点、临界点”的寻找和判定往往是正确解决问题的关键.
2.2 不同运动物体间依靠轻绳相互牵连
题型特点:物体间的相对运动关系靠轻绳牵连,不同于轻杆的地方在于它只能“拉”而不能“推”.
【例4】如图5所示,轻质长绳水平地跨在相距为2l的两个小定滑轮A,B上,质量为m的物块悬挂在绳上的O点,O与A,B两滑轮的距离相等.在轻绳两端C,D分别施加竖直向下的恒力F=mg.先托住物块,使绳处于水平拉直状态,静止释放物块,在物块下落过程中,保持C,D两端的拉力F不变.求物块下落过程中的最大速度vm和最大距离Hm.
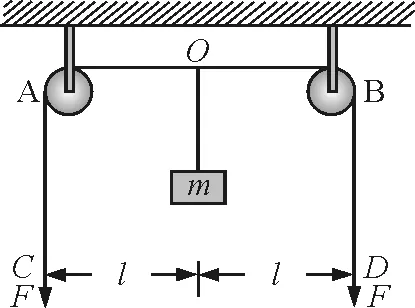
图5
解析:物体所受合外力为零时,加速度为零,此时物体有最大速度vm,设此时物块下降距离是h.
又因绳中拉力F恒为mg,所以,此时悬点所受的三个拉力的方向成夹角2θ=120°.
由图6可知
当物块下落h时,C端上升距离
克服C端恒力F做功
由动能定理得
解得最大速度
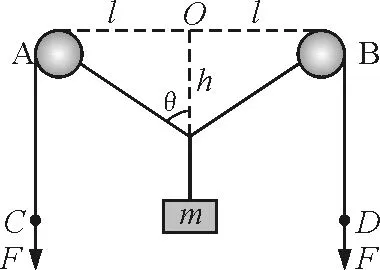
图6
物块下落最大距离Hm时,系统速度为零,由机械能守恒可得
所以

点评:处理该类问题时要注意牵连物沿绳方向速度相等,及由于物体运动造成的绳长变化和物体运动距离之间的几何牵连关系.
3 轻质弹簧连接体
题型特点:物体间依靠轻质弹簧连接,注意弹簧弹性势能的变化、代换关系.
【例5】如图7所示,质量为m1的物体A经一轻质弹簧与下方地面上质量为m2的物体B相连,弹簧的劲度系数为κ,A,B都处于静止状态.一条不可伸长的轻绳绕过轻滑轮,一端连物体A,另一端连一轻挂钩.开始时各段绳都处于伸直状态,A上方的一段绳沿竖直方向.现在挂钩上挂一质量为m3的物体C并从静止状态释放,已知它恰能使B离开地面但不继续上升.若将C换成另一个质量为(m1+m3)的物体D,仍从上述初始位置由静止状态释放,则这次B刚离地时D的速度大小是多少?已知重力加速度为g.
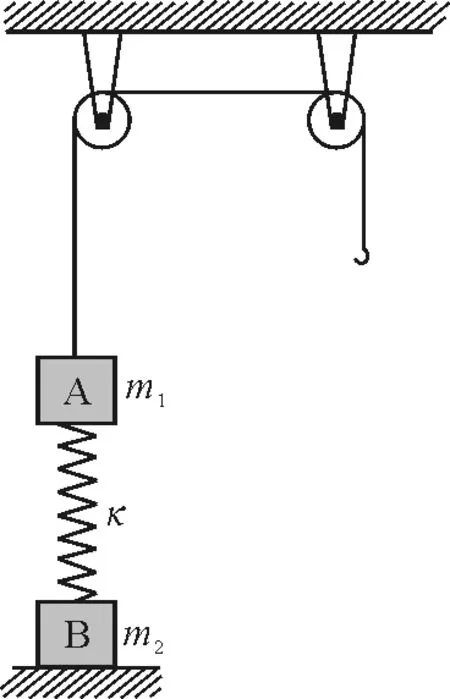
图7
解析:开始时,A,B静止,设弹簧压缩量为x1有
κx1=m1g
(9)
挂C并释放后,C向下运动,A向上运动,设B刚要离地时弹簧伸长量为x2,有
κx2=m2g
(10)
B不再上升,表示此时A和C的速度为零,C已降到最低点.由机械能守恒,与初始状态相比,弹簧弹性势能的增加量为
ΔEp=m3g(x1+x2)-m1g(x1+x2)
(11)
C换成D后,当B刚离地时,弹簧弹性势能的增量与前一次相同,设此时A,D的速度大小为v,由能量关系得
(m3+m1)g(x1+x2)-m1g(x1+x2)-ΔEp
(12)
由式(9)~(12)得
点评:(1)弹簧的弹性势能与弹簧的劲度系数κ和弹簧长度变化量有关,同一弹簧长度变化量相同时,储存的弹性势能大小相等.
4 软绳 软链 液体类
题型特点:因为“软”,物体在运动过程中不存在因碰撞导致的机械能损失.
【例6】如图8所示,AB为光滑的水平面,BC是倾角为α的足够长的光滑斜面(斜面体固定不动).AB,BC间用一小段光滑圆弧轨道相连.一条长为L的均匀柔软链条开始时静止放在ABC面上,其一端D至B的距离为L-a.现自由释放链条,则链条的D端滑到B点时,链条的速率为多大?
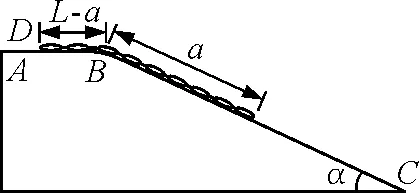
图8
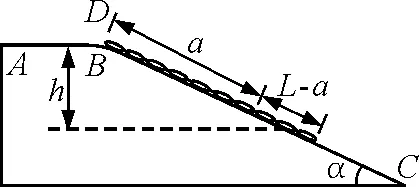
图9
解析:链条机械能守恒.水平面上链条长度减少,斜面上的长度增加.设链条质量为m.初、末状态重力势能的变化,可等效认为是由于L-a段的重心直接下降高度h引起的,如图9,且有
并且该部分的质量为
重力势能的减少量为
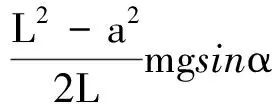
(13)
软链动能增量为
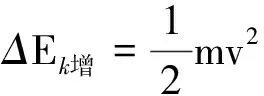
(14)
由机械能守恒得
ΔEp减=ΔEk增
(15)
由式(13)~(15)得
解得
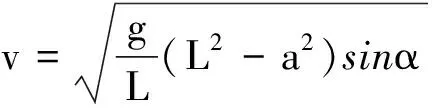
点评:本题利用“等效平移法”计算出了链条重力势能的减少量,也可以通过确定链条初、末状态重心的位置计算重力势能的减少.
