注意保守力“做功与路径无关”的“陷阱”

2013-01-11冯海燕

物理通报 2013年12期

冯海燕

(大庆实验中学黑龙江大庆 163316)

我们知道,保守力做功与路径无关，只取决于初、末位置.常见的保守力场,如重力场、电场等，在无界场中学生已经运用自如，但是在有界保守力场中，如果还机械套用上述结论，就容易犯错.在某次考试中出了如下一道题，从学生的答题情况看，结果很不理想.现具体说明.

【例1】如图1所示，半径R的环形塑料管竖直放置，AB为该环的水平直径，且管的内径远小于环的半径.环的AB及其以下部分处于水平向左的匀强电场中，管的内壁光滑.现将一质量为m，带电荷量为+q的小球从管中A点由静止释放，已知qE=mg，求:

(1)小球释放后，第一次和第二次经过最高点C时对管壁的压力之比;

(2)小球释放后，第一次经过最低点D和最高点C时对管壁的压力之比.

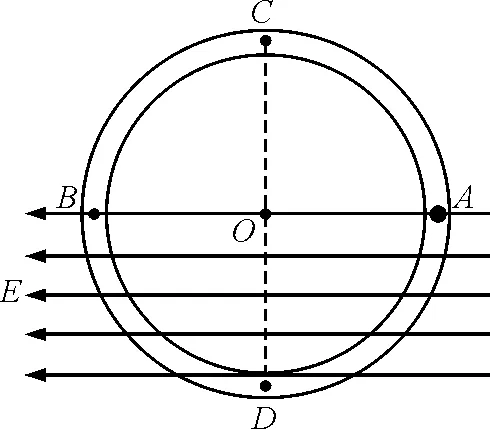
图1

常见错误解析：(1)小球两次到达同一点C，其电势能、重力势能都相同，故动能也相同.所以,小球两次到达C点时对管壁的压力也相等，可得比值为1∶1.两次均有

qE=mg

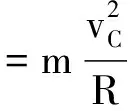
得

分析可得

对内壁有压力.

(2)小球第一次到达D点时

qE=mg

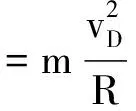
得

小球第一次到达C点时

qE=mg

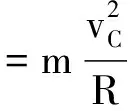
得

正确解析:(1)小球第一次到达最高点C

qE=mg

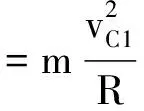
得

第二次到达最高点C

qE=mg

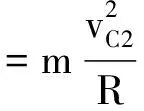
得

(2)小球第一次到达D点时

qE=mg

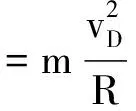
得

错因分析:“保守力做功与路径无关，只取决于初、末位置”适用于在保守力场区内的运动.如果有跳出场区的过程，则不再适用.在大学的电磁学教材中有如下的叙述，静电场强沿任一闭合曲线的环路积分为零[1].可见，跳出了电场，便形成不了上述的环路积分.

有些题目，原题答案就犯了上述错误，若不及时更正会误导学生.

【例2】如图2，在xOy平面上x<0的区域内存在一垂直纸面向外的匀强磁场，磁感应强度大小为B，OA是过原点的一条直线，与y轴正方向的夹角为θ=60°．在x>0的区域有一与OA平行的匀强电场，场强大小为E．现有一质量为m，电量为q的带正电的粒子(重力不计)从直线OA上的某处P点由静止释放后，经O点进入磁场，经过一段时间后恰能垂直OA到达OA上的Q点(电场方向以及P点、Q点位置在图中均未画出)．求：

(1)P点的坐标；

(2)粒子从P点释放到垂直OA到达Q点所用的时间；

(3)PQ之间的距离.