对平行力分解问题的进一步探究
2013-01-11顾俊琪
顾俊琪
(盐城市教育科学研究院 江苏 盐城 224002)
1 问题再现
如图1所示,把一根直尺水平地放在两个食指上,然后让两个食指尽量靠拢.结果发现两个食指不可能同时在直尺下滑动,而是其中一个食指先在直尺下面滑动,然后,另一个食指再在直尺下面滑动,如此交替地继续下去.为什么两个手指在直尺下面会交替地滑动?
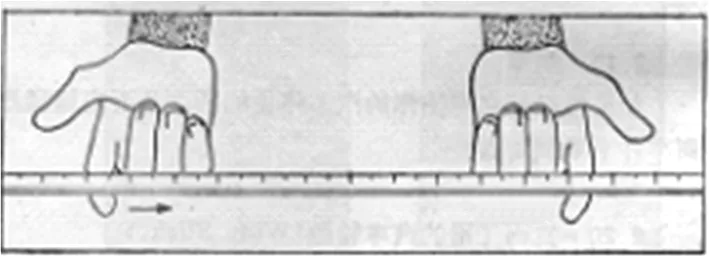
图1 两食指水平托一直尺,然后两食指相互靠拢
2 定性解释
一个手指先在直尺下方滑动,二者之间的摩擦力为滑动摩擦力,而此时直尺与另一个手指未发生相对滑动,是因为其最大静摩擦因数较大.手指受到的摩擦力的大小不仅与摩擦因数有关,而且还与直尺压在手指上的压力有关.当运动的手指向直尺中心滑动时,直尺压在这个手指上的压力变得愈来愈大,压在另一个手指上的压力变得愈来愈小.最后,运动手指作用在直尺上的摩擦力会变大,使另一个手指与直尺之间的静摩擦力超过了它们之间的最大静摩擦力,于是第一个手指停止了滑动,而另一个手指便开始滑动.这种交替进行的运动可以发生数次直到两手指都移到直尺中央为止.
3 数学推导
取一根质量分布均匀的直尺,重力大小为G,长度为l,重心C位于直尺中点处.假设两手指与直尺的动摩擦因数和最大静摩擦因数都相同,分别为μ和μ0.
如图2所示,假定左手指先滑动,此时右手指保持不动,整个过程可看成准静态,直尺满足一般物体平衡条件
(1)
N1+N2=G
(2)
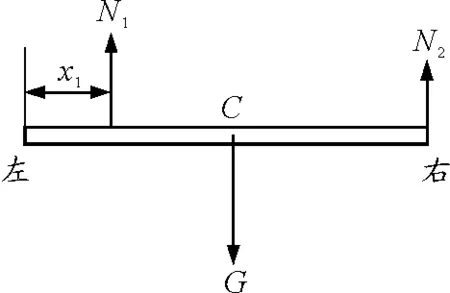
图2
由式(1)、(2)可以发现,左手指对直尺的支持力N1随移动距离x1的增大而增大,右手指对直尺的支持力N2随移动距离x1的增大而减小.这样,左手给直尺的滑动摩擦力会逐步增大,右手给直尺的最大静摩擦力会逐步减小,当满足μN1=μ0N2时,右手指开始滑动.
不难求得
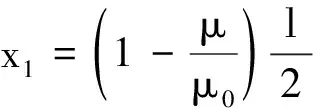
如图3所示,右手指开始滑动后,左手指不再移动,整个过程仍可看成准静态,直尺满足一般物体平衡条件
(3)
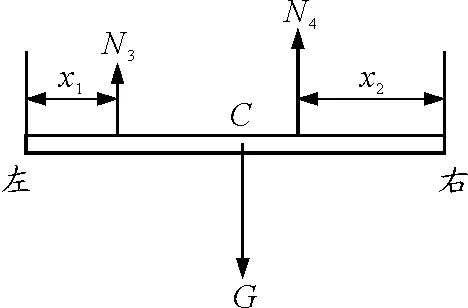
图3
再结合μN4=μ0N3可以求得,右手指到再次不动时移动的距离
以此类推,可以得到第n次移动手指停止时,离开直尺端点的距离
由于μ<μ0,所以当n→时,该结果表明,两手指最终停在直尺中点位置.
应该注意,如果直尺放在两手指间不再水平,有点倾斜的话,上述结论是不成立的.
4 实验验证
上述结论要得到实验验证并不简单.我们从实验室找到一根质量分布基本均匀的米尺,把它水平地放在两个食指上,使标有刻度的一面朝上,然后,让两个食指从两端点开始向中间滑动,记录下有关数据,见表1.
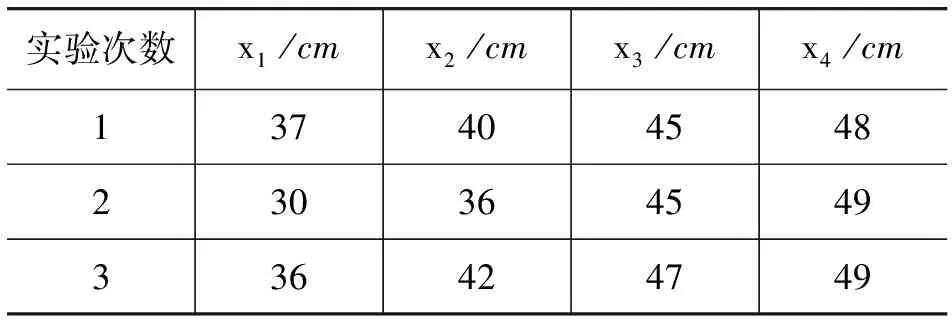
表1 记录的有关数据
表1中的数据表明,手指移动距离并不像数学推导得那样具有规律性,出现结果不稳定性的主要原因是手指与直尺之间的摩擦因数不稳定.
笔者从50多根米尺中挑选出粗糙程度相对均衡的一根,按照有关要求重新实验,得到表2数据(仍有少数数据存在漂移,表中已经剔除).
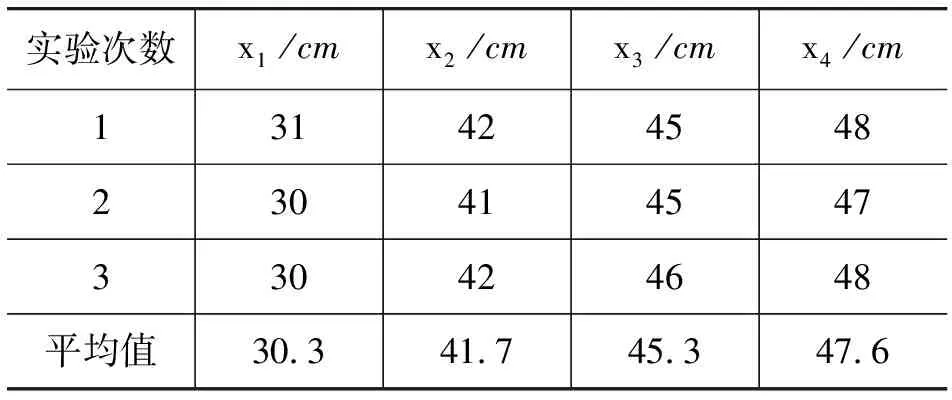
表2 采用粗糙程度均衡的米尺所测数据
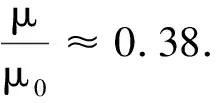
5 问题讨论
(1)手指在直尺下的运动是否一定会交替进行?
根据上述研究不难发现,当手指与直尺之间比较光滑时,即手指与直尺之间的摩擦因数很小时,或者说,当手指与直尺之间动摩擦因数与静摩擦因数非常接近时,手指在直尺下运动的先后顺序就有随机性,甚至会出现同时运动的现象.在实际生活中,以上两种情况并不多见,看到的基本是交替进行的.如果控制好条件,在具体实验中可能会出现并非交替运动的情形.
(2)开始时,位于直尺两端点的手指谁先滑动?
理论上讲,只有两手指与直尺之间的最大静摩擦力存在差异,才会出现先后滑动的情况.
如果两手指位于质量均匀的直尺对称的两端点上,且手指与直尺之间最大静摩擦因数完全相同,两手指不应该有一个先滑动.所以,先滑动的手指与直尺的最大静摩擦因数应该偏小,或者该手指距直尺重心的距离稍远些.
(3)在手指交替运动过程中,直尺受到的摩擦力究竟如何?
在手指交替运动过程中,直尺一直受到两个摩擦力的作用,一个是运动手指给予的滑动摩擦力,另一个是静止手指给予的静摩擦力.由于直尺是准静态的,所以这两个力始终相等.根据滑动摩擦力公式f=μFN,运动手指与直尺之间的摩擦力随着压力的增大而增大,因而静止手指与直尺之间的静摩擦力也增大,但手指与直尺之间的最大静摩擦力却在减小,当静摩擦力达到最大时,静止手指开始运动.
(4)如果直尺质量分布不均匀,手指最终应该停在何处?
如图4所示,根据数学推导过程中的有关公式可以推知,如果直尺质量分布不均匀,左手指移动距离将越来越趋近于l1,右手指移动距离将越来越趋近于l2,所以,手指最终应该停在直尺重心处.考虑一个极限情况,左手指已经到达直尺的重心位置,此时右手指无论怎样移动,直尺都不会移动,因为右手指不受直尺的压力作用,也就不会给直尺施加摩擦力的作用.
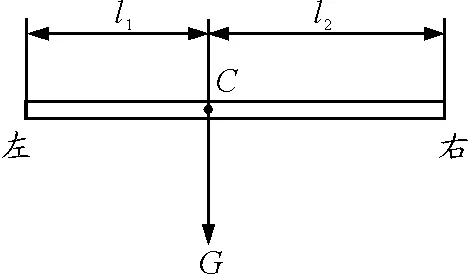
图4
以上探究过程思考尚不够完备,欢迎同仁赐教.
参考文献
1 (美)Jearl Walker.生活中的物理学.徐婉华,叶庆桐译.北京:科学普及出版社,1984
