基于最优梯度法的MPPT全数字控制仿真

林文立 刘治钢 马亮

（北京空间飞行器总体设计部，北京 100094）

1 引言

目前，大多数航天器功率调节系统都是通过设定固定的参考工作点对电压进行调节，在全生命周期内不能最大限度地利用太阳电池阵输出功率，而通过采用太阳电池阵最大功率点跟踪（Maximum Power Point Tracking，MPPT）技术，可以保证系统自动跟踪太阳电池阵最大功率输出，使电源系统在相同的太阳电池和蓄电池配置的条件下，输出更多的能量，从而减少了整星的体积和质量，这种拓扑结构在大功率航天器［1］或太阳光照条件变化剧烈的情况应用，效果尤其明显。国外许多深空探测器，如“火星快车”（Mars Express）、“金星快车”（Venus Express）、罗塞塔彗星探测器（Rossetta）、信使号探测器（Messenger）、贝皮·科伦坡水星探测器（Bepicolombo）的电源系统设计均采用了 MPPT 拓扑［1-8］，而目前国内研究该技术在航天器上的应用还比较少［9］。

文献［10-11］提到采用比较器、触发器、采样保持等模拟电路实现增量电导法MPPT 控制，但是由于受电路／芯片参数漂移等因素影响，最大功率点跟踪控制的准确度有限（约96%），并且难以满足未来数字化、智能化电源管理与控制的需求，因此目前业内倾向于采用软件算法实现，但是由于航天器的特殊应用条件及高可靠性要求，可在空间应用的算法研究还很少。

本文提出一种基于最优梯度法的MPPT 全数字控制方法，它具有最大功率点跟踪控制准确度高、易于数字编程实现等特点；介绍了MPPT 算法的数字控制逻辑，并建立Matlab／simulink 仿真模型对所提出的MPPT 控制策略进行了模拟工况仿真，最后给出了仿真分析结果。

2 最优梯度法的寻优机理

最优梯度法的基本思想，是选取目标函数的正梯度方向作为每步迭代的搜索方向，逐步逼近函数的最大值，它保留了扰动观察法的各种优点，同时由一个类似动态的变化量来改变在太阳能输出功率曲线上电压的收敛速度。

如图1所示，Vk-1，Vk，Vk＋1分别代表k-1时刻、k时刻、k＋1时刻的参考电压值，图1（a）中当工作点位于最大功率点左侧且远离峰值点时，电压以较大的幅度迭代增加（Vk-1→Vk），当工作点位于最大功率点附近时，由于此时曲线斜率较小，则提供较小的变化量（Vk→Vk＋1）。反之，图1（b）中当工作点位于最大功率点右侧并远离峰值点时，电压也以较大的幅度迭代减少（Vk-1→Vk），当工作点接近最大功率点时，则提供较小的变化量（Vk→Vk＋1）。

最优梯度法可改善传统扰动观察法在最大功率输出点附近振荡追逐的缺点，同时也有较好的动态响应速率。

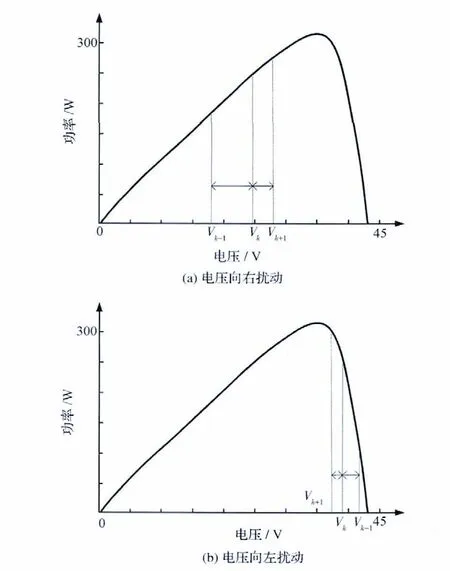
图1 利用最优梯度法进行最大功率点跟踪控制过程的示意图Fig.1 Scheme for the MPPT using optimized gradient method

3 基于最优梯度法的太阳电池阵MPPT全数字控制方法

图2分别为恒温不同光强与恒光强不同温度条件下，太阳电池阵功率-电压输出特性曲线簇，其中，P 为输出功率，V 为输出电压，并且在一定的光强和温度环境下，太阳电池阵只有一个工作点输出功率最大，即峰值功率点Pmax。由图2（a）可知，在恒温不同光强条件下，随着光强增加，太阳电池阵输出的最大功率Pmax逐渐增大；由图2（b）可知，在恒光强不同温度条件下，随着温度上升，太阳电池阵输出的最大功率Pmax逐渐降低。

由此可见，在某一光照、温度条件下，太阳电池阵的P-V 输出特性曲线是一条单极值曲线，而该曲线的最大值点可通过最优梯度法进行寻优。为满足未来空间电源智能化管理与控制需求，充分利用数字信号处理器强大的运算能力和信息处理能力，本文提出一种新型的基于最优梯度法的MPPT 全数字控制策略，控制逻辑如图3所示。

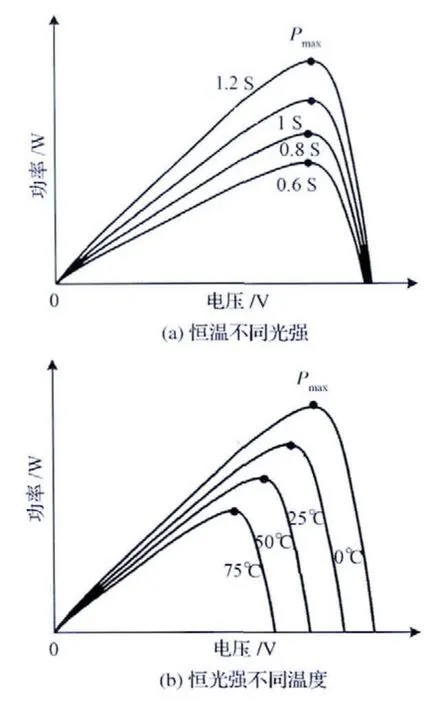
图2 太阳电池阵P-V 曲线簇Fig.2 P-V curves for the solar array

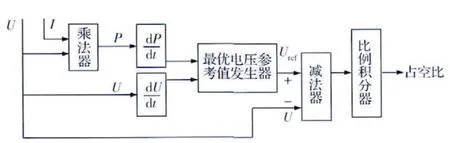
图3 基于最优梯度法的MPPT 控制策略框图Fig.3 Diagram for MPPT control strategy based on the optimized gradient method

图3中，通过采集太阳电池阵的直流电压U 和直流电流Ⅰ，二者相乘计算出当前太阳电池阵的输出功率P，然后分别计算P、U 对时间t的微分值dP／dt，dU／dt，进而计算：

由图1可知，当dP／dU＞0时，工作点处于最大功率点的左侧，当dP／dU＜0时，工作点处于最大功率点的右侧，并且dP／dU 的绝对值越大，则表示其距离最大功率点越远；只有当dP／dU≈0时，工作点处于最大功率点附近。

图3中“最优电压参考值发生器”具体逻辑如下：

（1）如果dP／dU≈0，那么

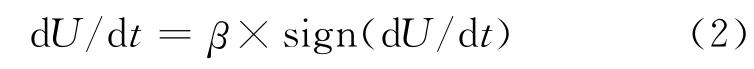
（2）否则，直接计算

（3）然后

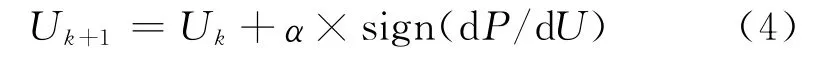
式中：α，β均为可调常数；sign（）为取符号函数；Uk＋1即为图3中给出的下一时刻太阳电池阵电路输出电压参考值Uref，它与实际电压U 的差值，经比例积分器调节后形成阵列功率调节器（APR）电路功率开关管的驱动脉冲占空比，通过对APR 功率开关管的导通、关断控制实现太阳电池阵MPPT 控制。

4 仿真分析

4.1 仿真模型

利用Matlab／simulink 软件，搭建太阳电池阵MPPT 控制电源系统仿真模型，如图4 所示，主要包括太阳电池阵模块（SA）、MPPT 控制模块、Super-buck DC／DC变换器电路（主要由电感L、L1，电容C、C1，功率开关管M，二极管D 组成）、负载等。

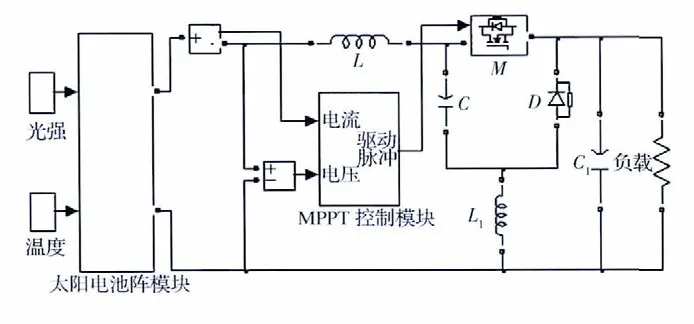
图4 太阳电池阵MPPT 控制电源系统仿真模型Fig.4 Simulation model for the SA MPPT control power system

其中，太阳电池阵模块采用纯数学建模方法，具体参考下式：

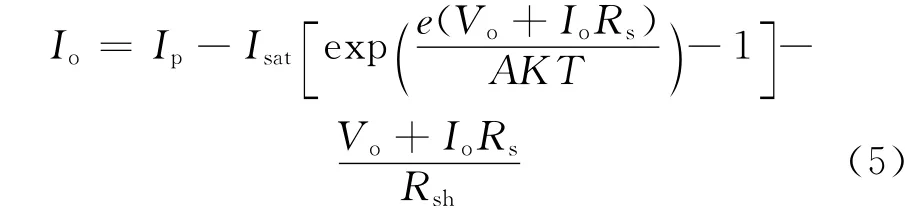
式中：A 为曲线拟合常数；Rs为电池串联电阻；Rsh为电池并联电阻；Ⅰsat为二极管反向饱和电流密度（A／m2）；Ⅰp为光导电流；e为电子电荷（1.6×10-19C）；K 为玻耳兹曼常数（1.38×10-23J／K）；T 为电池绝对温度（K）；Ⅰo为电池输出电流；Vo为电池输出电压。

MPPT 控制模块如图5所示，输入信号是太阳电池阵输出电压V 和电流Ⅰ，经基于最优梯度法的MPPT 运算迭代处理后，最终输出DC／DC 变换器功率管的驱动脉冲控制信号，保证始终跟踪太阳电池阵最大功率点，具体实现逻辑详见第3节。

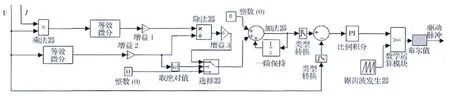
图5 Matlab／simulink中MPPT 控制模型Fig.5 MPPT control model in Matlab／simulink

4.2 仿真结果与分析

为了验证MPPT 的跟踪能力，设定太阳电池阵分别在以下两种条件下工作。

条件1：工作温度85°C，开路电压33V，最大功率点电压30V，电流6A，最大功率点功率180 W；

条件2：工作温度35°C，开路电压51V，最大功率点电压44V，电流6.82A，最大功率点功率300 W。

如图6所示，条件1工作温度85°C对应的太阳电池阵功率-电压（P-V）曲线为Curve-1，最大功率点设计为（30V，180 W）；条件2工作温度35°C 对应的太阳电池阵P-V 曲线为Curve-2，最大功率点设计为（44V，300 W）。

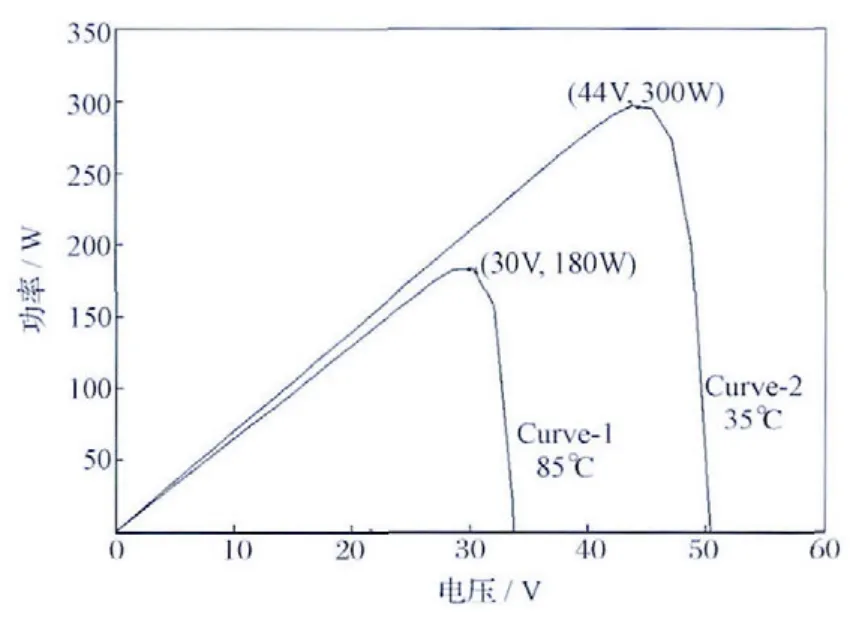
图6 35℃与85℃两种太阳电池阵P-V 曲线Fig.6 Two P-V characteristic curves of SA for simulation：Curve-1at 85℃，Curve-2at 35℃

仿真工况设定：初始t＝0s时，太阳电池阵按Curve-1工作，t＝0.5s后，切换为按Curve-2工作。图7所示为最终仿真获得的波形，其中，变量Vin为太阳电池阵的输出电压（也即为功率变换器的输入电压）；Vref为MPPT 模块内部产生的太阳电池阵输出电压参考值；Vdelta为Vref与Vin之间的差值，通过对差值Vdelta的比例积分，产生具有特定占空比、能够驱动后级DC／DC 变换器中功率开关管的驱动脉冲；Pin为太阳电池阵的输出功率。

工作过程描述如下：系统自t＝0s开始投入工作，初始时太阳电池阵特性曲线按Curve-1进行设置，图7（d）中输出功率Pin从0开始逐步增大，在t＝0.1s左右时，MPPT控制器搜索到当前曲线Curve-1的峰值功率Pin＝180 W 附近，此时图7（a）中Vin＝30V，符合图6所示的Curve-1最大功率点的设计值（30V，180 W）；在此之后t＝0.1s～0.5s区间内，MPPT 控制器保证了系统始终工作在当前曲线的峰值点附近；而在t＝0.5s时刻，太阳电池阵曲线由Curve-1切换为Curve-2，由于两曲线的峰值功率点发生了变化，MPPT 控制器开始投入工作，图7（b）中MPPT 模块内产生的太阳电池阵输出电压参考值Vref逐渐增加，图7（c）中Vref与Vin二者差值也相应发生变化，开始重新搜索新的最大功率点的过程，如图7（d）所示，大约在t＝0.7s时，搜索到当前曲线Curve-2的峰值功率Pin＝300 W 附近，此时图7（a）中Vin＝44V，符合图6所示的Curve-2最大功率点设计值（44V，300 W）。

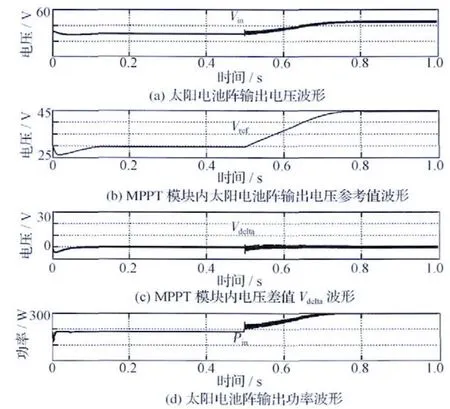
图7 MPPT 控制仿真波形Fig.7 Simulation waveforms for MPPT control

与图7相对应，图8所示为太阳电池阵特性曲线由Curve-1变化为Curve-2的最大功率点跟踪轨迹。从图8中可以看出，工况转换之前，太阳电池阵输出特性按Curve-1曲线，最大功率点跟踪轨迹为“A →B →C →D →E →F”，F点即为Curve-1曲线的最大功率点（30V，180 W），t＝0.1s～0.5s区间内，MPPT 控制器始终保证系统工作在F 点附近极小范围内摆动；在t＝0.5s时刻，太阳电池阵曲线由Curve-1设置为Curve-2，由于两曲线的最大功率点发生了变化，MPPT 控制器开始投入工作并重新搜索新的峰值点，最大功率点跟踪轨迹为“F→G →H →I→J→K →L”，L 点即为Curve-2曲线的最大功率点（44V，300 W），此后MPPT 控制器始终保证系统工作在L 点附近极小范围内摆动。经计算，两种工况转换前后，最大功率点跟踪控制准确度均达到99%以上，具有较高的最大功率点跟踪精度。

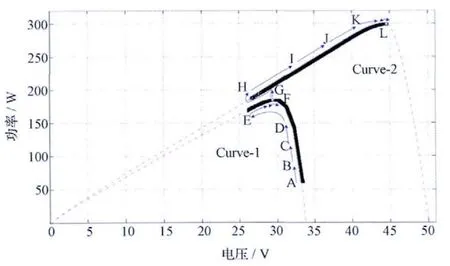
图8 最大功率点跟踪轨迹Fig.8 MPPT tracking curve

5 结论

由于空间飞行器特殊应用条件及高可靠性要求，可在航天器上应用的MPPT 数字控制算法研究还很少，目前，仅有少数采用基于模拟硬件电路实现增量电导法MPPT 的先例，然而，硬件电路不可避免受自身参数漂移影响，从而导致最大功率点跟踪精度有限。为满足未来空间电源智能化管理与控制需求，本文提出一种新型基于最优梯度法的MPPT全数字控制策略，并建立仿真模型对所提出的MPPT 控制策略进行了模拟工况仿真，结果表明，本文所提出的MPPT 控制算法峰值功率跟踪准确度可达到峰值功率的99%以上，并且在任意工况条件下，均能够自主搜索并且快速跟踪到当前状态下的峰值功率点，其动态响应快、控制准确度高，可完全满足空间电源的应用要求。

（References）

［1］Croci L，Caccivio M.Electrical power system for GAIA［C］／／Proceedings of 8th European Space Power Conference.Constance：ESA，2008：386-392

［2］Tonicello F.The control problem of maximum point power tracking in power systems［C］／／Proceedings of the 7th European Space Power Conference.Paris：ESA，2005：9-13

［3］Loche D.Mars express and venus express power subsytem in-flight behaviour［C］／／Proceedings of 8th European Space Power Conference.Constance：ESA，2008：1-7

［4］Fiebrich H，Haines J E，Tonicello F.Power system design of the rosetta spacecraft［C］／／Proceedings of 2nd IECEC.Washington D.C.：AIAA，2004：1-7

［5］Dakermanji G，Person C，Jenkins J，et al.The messenger spacecraft power system design and early mission performance［C］／／Proceedings of the 7th European Space Power Conference.Paris：ESA，2005：1-8

［6］Lempereur V，Jauquet D，Labille JM，et al.Power conditioning and distribution unit of globalstar-2constellation［C］／／Proceedings of the 8th European Space Power Conference.Paris：ESA，2008：119-125

［7］Santoni F，Piergentili F.Design and test of a maximum power point tracking system for UNISAT-3microsatellite［C］／／55th International Astronautical Congress.Vancouver：IAC，2004：1-10

［8］Breier N，Kiewe B，Mourra O.The power control and distribution unit for the SWARM satellites［C］／／Proceedings of the 8th European Space Power Conference.Paris：ESA，2008：289-295

［9］刘治钢，蔡晓东，陈琦，等.采用MPPT 技术的国外深空探测器电源系统综述［J］.航天器工程，2011，20（5）：105-110 Liu Zhigang，Cai Xiaodong，Chen Qi，et al.Overview of space power system design using MPPT for deep space spacecraft［J］.Spacecraft Engineering，2011，20（5）：105-110（in Chinese）

［10］Jensen H，Laursen J.Power conditioning unit for Rosetta／Mars express［C］／／6th European Space Power Conference.Paris：ESA，2002：249-256

［11］Tonicello F.Power conditioning uint for Rosseta／Mars express-lessons learnt［C］／／6th European Space Power Conference.Paris：ESA，2002：185-192