敏捷卫星像移补偿残差计算及对成像影响分析

谢少波 秦冉冉

（上海卫星工程研究所，上海 200240）

1 引言

敏捷光学成像卫星是空间成像卫星中的一个重要发展方向，敏捷光学成像卫星的特点能够在平飞的基础上，快速实现俯仰机动、滚动机动以及俯仰加滚动同时机动等各种情况，卫星相机视轴可以灵活调整对地指向，因此可以适应多种工作模式［1］，与以往一维机动卫星不同的是其像移矢量计算模型更加复杂，敏捷光学成像卫星利用推扫成像，普遍采用了时间延迟积分电荷耦合器件（TDICCD）传感器［2］，以获得较高的图像信噪比，而TDICCD 相机需对像移进行精细对准匹配才能实现清晰成像。在工程上，主要采取的是通过卫星实现偏流角控制和相机实现行频控制，参考文献［3］给出了仅在卫星平飞星下点成像时的偏流角计算模型，参考文献［4］给出了忽略地球曲率的卫星偏流角计算模型，参考文献［5］给出了敏捷卫星仅在光轴上的偏流角计算模型，而不支持像面其它点的像移计算，以上均不能满足像移补偿残差工程计算需求。

未来敏捷卫星的发展是基于同轴相机和离轴相机等多种体制的［6］，对于像面上轴外像点的像移补偿及残差均需分析和控制，除了偏流角之外行频也不容忽视。

本文介绍了像移补偿残差机理及对调制传递函数（MTF）的影响，可以对相机光学视场内任意方向上，在卫星俯仰加滚动同时机动复杂姿态情况下的偏流角和行频进行计算和残差分析；结合具体设计案例进行了仿真分析，得到了其对MTF 的影响情况。本文的研究结果，可以对敏捷卫星相机设计及敏捷卫星总体设计提供参考。

2 像移补偿残差机理及对MTF的影响

卫星像移补偿残差主要有偏流角控制残差和行频控制残差，如图1所示。在工程应用中，卫星进行偏流角补偿时，一般以视轴上的偏流角作为主控偏流角，像面上的其它像点理论偏流角与实际主控偏流角之间均有一定误差，这个误差就是偏流角控制残差。另外，工程上卫星进行行频控制时，一般以每片TDICCD 为单位进行控制，每片TDICCD 工作行频是以其中心像点作为主控行频进行控制，而每片TDICCD 行像元数多达几千或者上万个，每片TDICCD 其它像元理论行频与实际主控行频之间存在一定误差，这个误差就是行频控制残差。对于离轴相机，其视轴与光轴并不重合，这种情况会使像移补偿残差计算变得更为复杂。

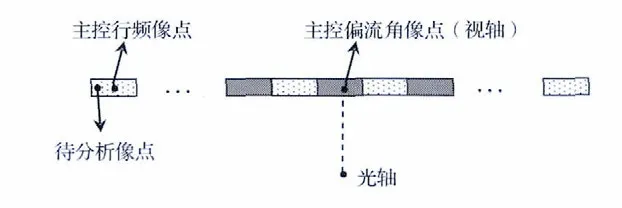
图1 像点不同引起的像移补偿残差Fig.1 Image shift compensation residue caused by different image points

偏流角控制残差引起的MTF 记作SMTF1，行频控制残差引起的MTF［7］记作SMTF2，总的像移失配引起的MTF见式（1）。

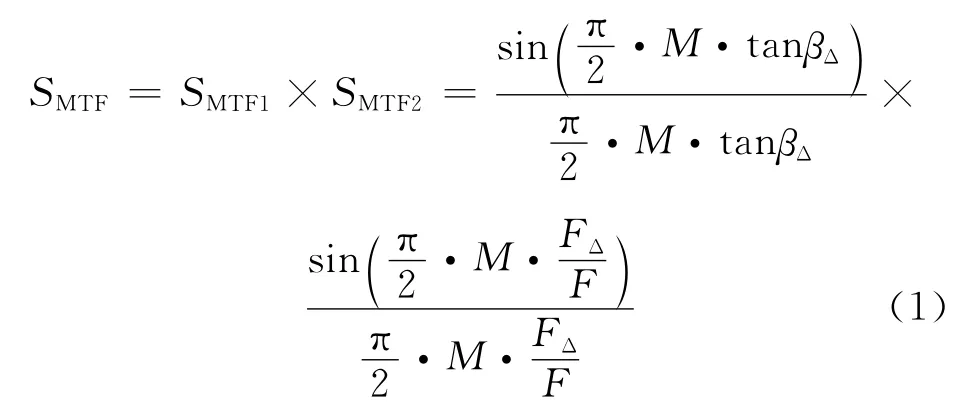
式中：M 为TDICCD 工作级数；βΔ为偏流角控制残差；FΔ为行频控制残差；F 为理论行频。式（1）是以像移特性为线性条件下使用的公式，地形的剧烈起伏或者卫星的随机振动，可能导致式（1）存在一定误差，在对海洋成像时不会受地形影响。

3 敏捷光学卫星像移补偿残差计算模型

敏捷光学卫星像移模型计算中，须用到卫星轨道及位置参数［8］、卫星姿态参数、地球参数、相机镜头参数、相机焦面参数。卫星轨道及位置参数有卫星质心到地心的距离H0，卫星质心到物面中心的距离即物距L，卫星轨道倾角i0，卫星轨道角速度Ω，卫星星下点纬度λ；卫星姿态参数有卫星本体系相对卫星轨道系按123转序［9］描述的滚动角φ、俯仰角θ、和偏航角ψ；地球参数有地球半径R，地球自转角速度ω；相机镜头参数有焦距f，相机焦面参数有像元尺寸p，像面像点坐标（xi，yi）［10］等，模型中须推算的中间变量有：在轨道平面内，卫星到降交点之间所对应的轨道中心角γ0，在降轨段γ0为-arcsin（sinλ／sini），在升轨段γ0为π＋arcsin（sinλ／sini），地物在地理坐标系中的位置坐标（xg，yg，zg），像面坐标系中横向和纵向像移速度分量分别为V′1、V′2。

本文建立了一种物像解析算法，在本算法中使用地理坐标系（地理坐标系由卫星轨道坐标系沿Z轴移动H 得到，Z 轴由卫星指向地心，H 为卫星地面高度）描述物坐标，而传统算法是以物面坐标系描述物坐标，本算法特点是物坐标原点与卫星姿态无关，因此能大量简化公式，本算法兼容平飞和一维机动模式，并已经通过与在轨卫星算法复核，所建立的物像方程见式（2）。

中间变量求解方程为

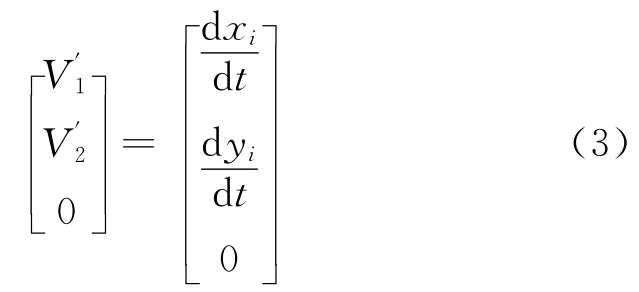
假如卫星实际控制偏流角为像面像点m，其在像面坐标系中坐标为（xm，ym），其像面坐标系中横向和纵向像移速度分量分别为，其偏流角为βm；实际控制行频为像面像点n，其像面坐标为（xn，yn），其像面坐标系中横向和纵向像移速度分量分别为，其行频为Fn；待实际分析的像点为k点，其像面坐标为（xk，yk），其像面坐标系中横向和纵向像移速度分量分别为其偏流角为βk，其行频为Fk，则偏流角和行频控制残差方程分别为：

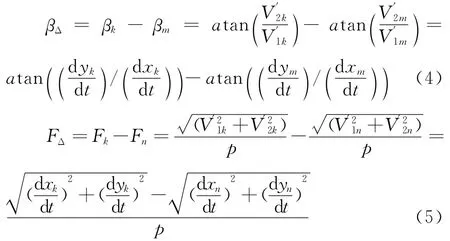
将式（2）微分获得式（3），再代入式（4）、（5）即可获解。

4 仿真计算

本文以一离轴角为4°、焦距为2.5m、飞行高度为1200km 的星载相机进行复杂姿态情况下的像移补偿残差及MTF仿真计算，仿真条件见表1。

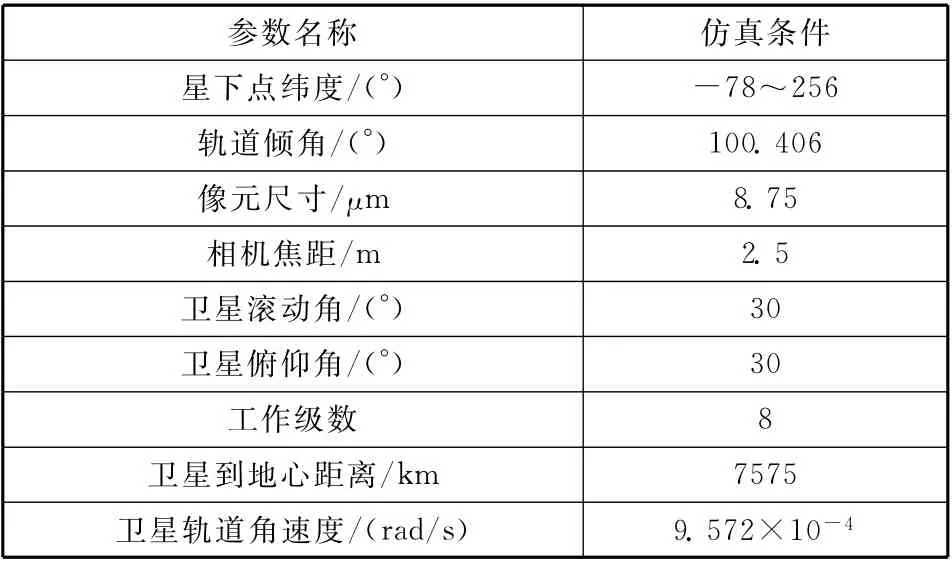
表1 仿真参数设置Table 1 Parameters’value for the simulation

因相机离轴角为4°，则主控偏流角像点像面坐标为（0.174 8 m，0 m），假如TDICCD 定制像元数为12 288个，焦面共选择7片TDICCD 拼接，则焦面长度为0.752 64m（对应地面幅宽365km），待分析像点像面坐标为（0.174 8m，0.376 32m），主控行频像点像面坐标为（0.174 8m，0.322 56m）。受轨道倾角的限制，卫星星下点能够覆盖南北纬78°以内的范围，在仿真中星下点纬度范围定义如图2所示。

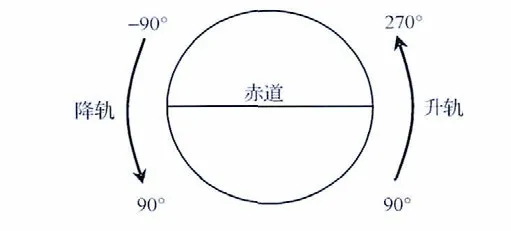
图2 星下点纬度范围定义Fig.2 Definition of the latitude range for subsatellite point

仿真结果如下：偏流角控制残差对MTF 影响见图3，行频控制残差对MTF 影响见图4，根据式（1）计算出来的像移补偿残差对MTF影响见图5。

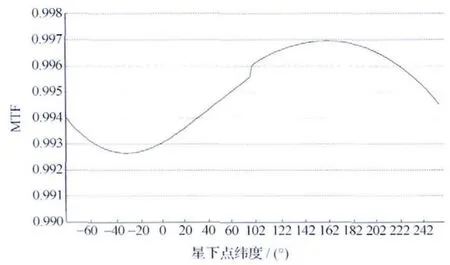
图3 偏流角控制残差对MTF的影响Fig.3 Influence on MTF of residue of bias-angle

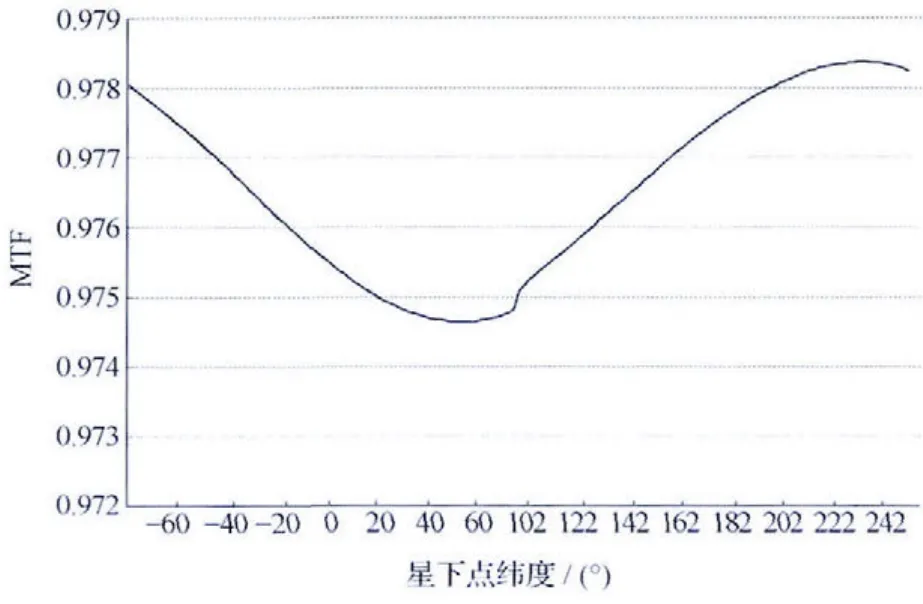
图4 12 288像元器件行频控制残差对MTF的影响Fig.4 Influence of residue of line rate on MTF for 12288pixels TDICCD

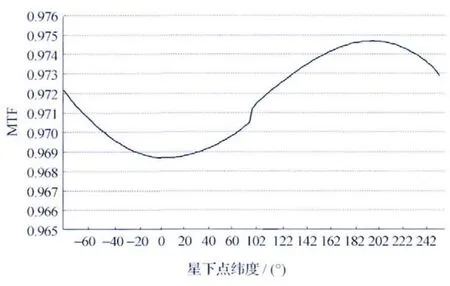
图5 12 288像元器件像移补偿残差对MTF的影响Fig.5 Influence of residue of image shift compensation on MTF for 12288pixels TDICCD

由图5可知，像移补偿残差对MTF 影响在降轨段赤道附近较大，在升轨段赤道附近较小，在全轨MTF均低于0.975，对成像是有一定影响的，且通过图3和图4可知，主要影响因素是行频控制残差，为了减少像移补偿残差对MTF 的影响，保证像移引起的MTF控制在0.98以上，对于敏捷光学卫星而言，可以减小卫星机动角度或者减小焦面长度，但这样均会影响卫星的总体性能。通过计算已经获知敏捷卫星MTF 受行频控制残差的影响更为严重，可以通过减少单片TDICCD 的像元数予以解决，缩小主控行频像点与待分析像点的距离，在仿真中如果定制的TDICCD像元数为6144个，则主控行频像点像面坐标为（0.174 80m，0.349 44m），在焦面长度不变的情况下待分析像点像面坐标仍为（0.174 8 m，0.376 32m），经仿真行频控制残差对MTF 的影响见图6，像移补偿残差对MTF 的影响见图7，可见，单片TDICCD 像元数的减少对提高MTF 明显，像移补偿MTF可以达到0.986以上。

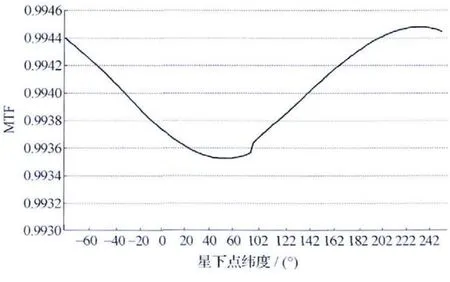
图6 6144像元器件行频控制残差对MTF的影响Fig.6 Influence of residue of line rate on MTF for 6144pixels TDICCD

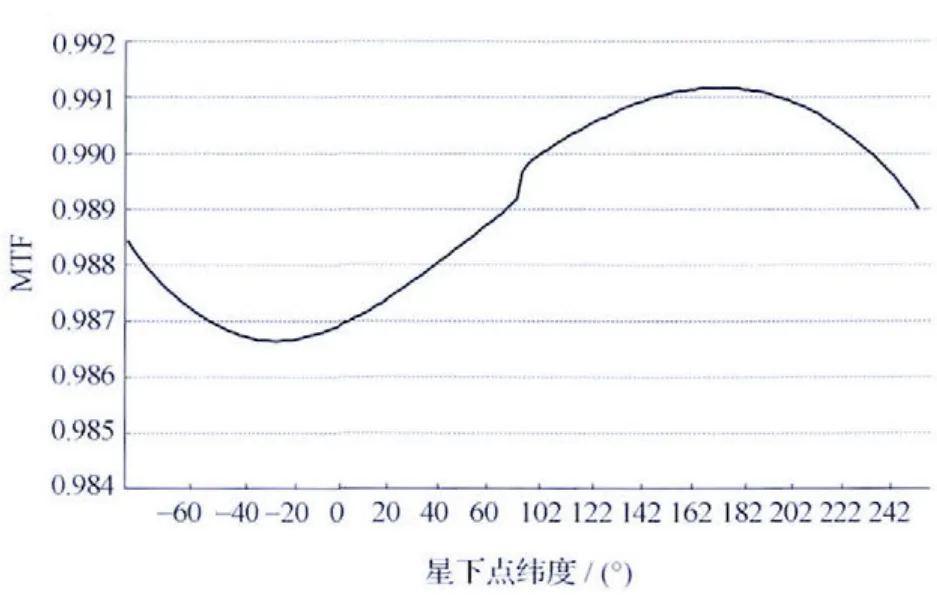
图7 6144像元器件像移补偿残差对MTF的影响Fig.7 Influence of residue of image shift compensation on MTF for 6144pixels TDICCD

5 结束语

本文计算了敏捷光学成像卫星在复杂姿态下的偏流角和行频像移补偿后的残差情况，及残差对MTF的影响，并举例给出了仿真数据及曲线，为了达到理想的在轨清晰成像要求，保证像移引起的MTF在0.98以上，对敏捷卫星相机行频控制残差应予以重视，在工程中宜选用像元数较少的TDICCD 器件。本文推导的偏流角和行频计算公式，可以应用在敏捷卫星的工程中，偏流角和行频控制残差方程，可以作为分配相机焦面长度（对应卫星成像幅宽）及卫星最大工作机动角度的依据。

（References）

［1］张新伟.敏捷遥感卫星工作模式研究［J］.航天器工程，2011，20（4）：32-38 Zhang Xinwei.Research on working mode of remotesensing satellite with agile attitude control［J］.Spacecraft Engineering，2011，20（4）：32-38（in Chinese）

［2］史磊，金光，安源，等.一种遥感相机的CCD 交错拼接方法研究［J］.红外，2009，30（1）：12-15 Shi Lei，Jin Guang，An Yuan，et al.Research on a mechanical interleaving stitching method of CCDs for remote sensing camera［J］.Infrared，2009，30（1）：12-15（in Chinese）

［3］王志刚.高分辨率卫星遥感图像的偏流角及其补偿研究［J］.宇航学报，2002，23（5）：39-42 Wang Zhigang.Study on satellite remote sensing high resolution image bias-angle and its compensation［J］.Journal of Astronautics，2002，23（5）：39-42（in Chinese）

［4］谢少波，周伟敏，张嵬.离轴三反（TMA）相机在轨成像的偏流角计算与控制［J］.上海航天，2012，29（1）：19-22 Xie Shaobo，Zhou Weimin，Zhang Wei.Calculation and control for the deviant angle of TMA camera on satellite［J］.Aerospace Shanghai，2012，29（1）：19-22（in Chinese）

［5］景泉.敏捷卫星偏流角计算模型研究［J］.航天器工程，2012，21（4）：16-20 Jing Quan.Research on computation model of bias angle for agile satellite［J］.Spacecraft Engineering，2012，21（4）：16-20（inChinese）

［6］徐亮，赵建科，周艳，等.长焦距、大视场空间观测相机光学系统设计［J］.光学与光电技术，2010，8（6）：64-66 Xu Liang，Zhao Jianke，Zhou Yan，et al.Optical design of the space observation camera with long focal length and wide field of view［J］.Optics ＆Optoelectronic Technology，2010，8（6）：64-66（in Chinese）

［7］马天波，郭永飞，李云飞.科学级TDICCD 相机的行频精度［J］.光学精密工程，2010，18（9）：2028-2035 Ma Tianbo，Guo Yongfei，Li Yunfei.Precision of row frequency of scientific grade TDICCD camera［J］.Optics and Precision Engineering，2010，18（9）：2028-2035（in Chinese）

［8］章仁为.卫星轨道姿态动力学与控制［M］.北京：北京航空航天大学出版社，1998：1-24 Zhang Renwei.Satellite attitude and orbit dynamics and control［M］.Beijing：Beijing University of Aeronautics and Astronautics Press，1998：1-24（in Chinese）

［9］李德仁，周月琴，金为铣.摄影测量与遥感概论［M］.北京：测绘出版社，2001：22-27 Li Deren，Zhou Yueqin，Jin Weixi.An introduction to photogrammetry and remote sensing［M］.Beijing：Surveying and Mapping Press，2001：22-27（in Chinese）

［10］王家骐，于平，颜昌详，等.航天光学遥感器像移速度矢计算数学模型［J］.光学学报，2004，24（12）：1585-1589 Wang Jiaqi，Yu Ping，Yan Changxiang，et al.Space optical remote sensor image motion velocity vector computational modeling［J］.Acta Optica Sinica，2004，24（12）：1585-1589（in Chinese）