3层胶结复合梁的应力分析与试验研究

2013-01-06任永臻集美大学机械工程学院福建厦门361021

长江大学学报(自科版) 2013年7期

任永臻（集美大学机械工程学院，福建厦门361021）

为了提高梁的强度，可以将几根梁组合在一起而形成胶结复合梁。胶结复合梁在水利、建筑、机械等领域应用较广，但其弯曲正应力分布规律与单根梁不同。有关2层胶结复合梁的应力分析与试验验证已有学者进行了研究［1］。下面，笔者对3层胶结复合梁承受纯弯曲变形时的正应力分布规律进行研究，推导出中性层的位置及沿横截面高度的正应力理论计算公式，然后利用应变电测法对推导结果进行试验验证❶。

1 理论分析

将纯弯曲情况下材料尺寸相同的3层矩形截面胶结复合梁作为计算模型（见图1），其中上梁的弹性模量为E1、横截面面积为A1；中梁的弹性模量为E2，横截面面积为A2；下梁的弹性模量为E3、横截面面积为A3，A1=A2=A3；梁长、梁宽和梁高分别为L、b和h，在其纵向对称面内，承受弯矩M的作用，且平面假设与单向假设均成立。

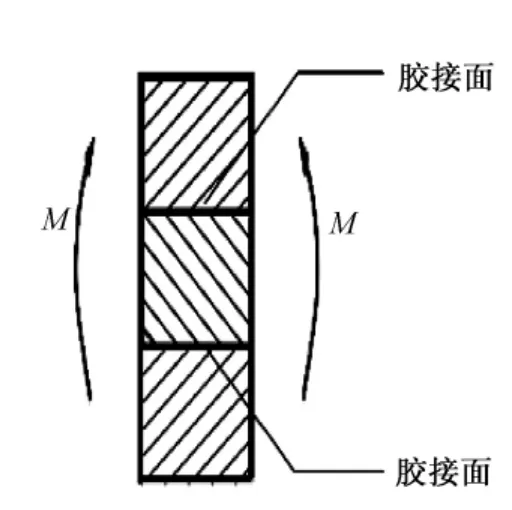
图1 3层胶结复合梁模型

1．1 几何、物理与静力学关系分析

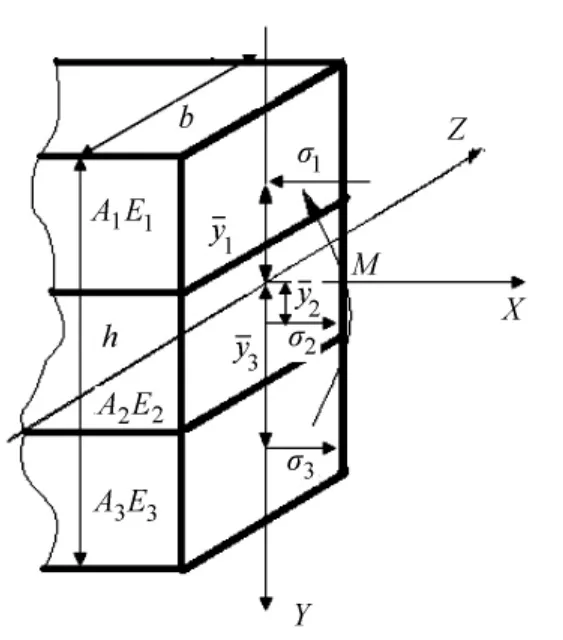
图2 3层胶结复合梁截面坐标及受力分析图

坐标系的建立如图2所示。以横截面的对称轴为Y轴，且向下为正；以中性轴为Z轴，但中性轴的位置尚待确定；在中性轴尚未确定之前，X轴只能暂时认为是通过原点的横截面的法线。

1）变形几何关系根据平面假设可知，横截面上y处的纵向正应变为［2］：

式中，ε表示纵向正应变；y表示离中性层的距离，mm；ρ表示中性层的曲率半径，mm。

2）物理关系由胡克定律可知，弯曲正应力σ为：

式中，E为材料的弹性模量，MPa。

将式（1）带入式（2），可以得到不同材料区的弯曲正应力：

式中，σ1、σ2、σ3分别为材料E1、E2、E3上的纵向正应力，MPa。

3）静力学平衡关系由微内力σ·dA组成的垂直于横截面的空间平行力系，只可能简化成3个内力分量，即平行于X轴的轴力∑Fx、对Y轴和Z轴的力偶矩∑My和∑Mz。横截面上的内力应与截面左侧的外力平衡（见图2），由静力学平衡关系可以得出：

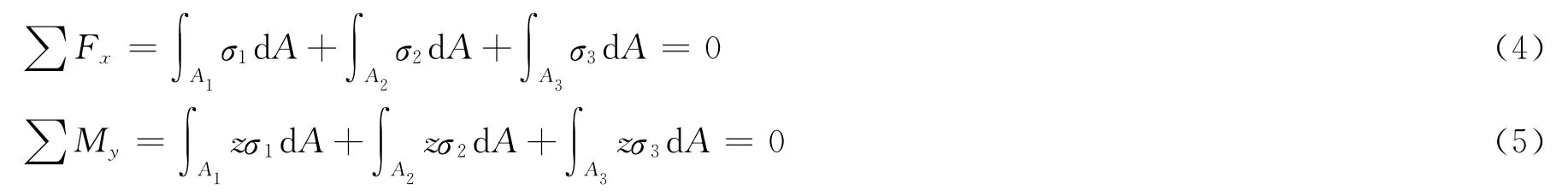
横截面上的内力系最终只归结为1个力偶矩∑Mz。在纯弯曲情况下，截面左侧的外力只有对Z轴的力偶M：

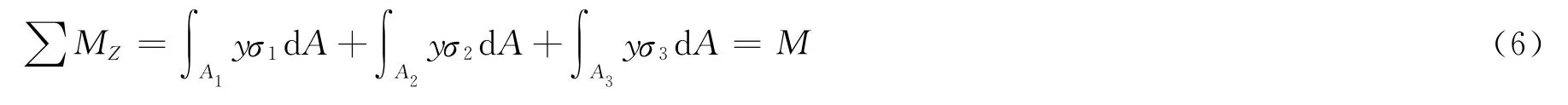
1．2 确定中性层位置

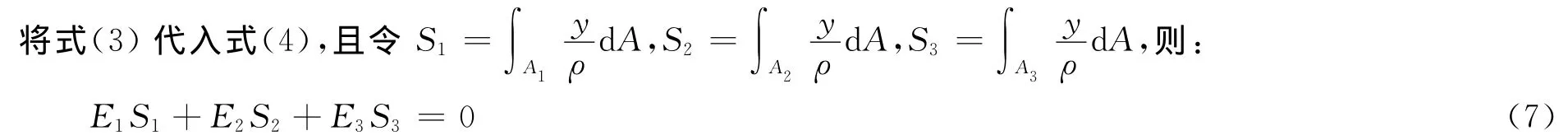
式中，S1、S2、S3分别为横截面的部分面积A1、A2、A3对中性轴的静矩。

设截面A1、A2和A3的形心纵坐标分别为y¯1、y¯2与y¯3，则：

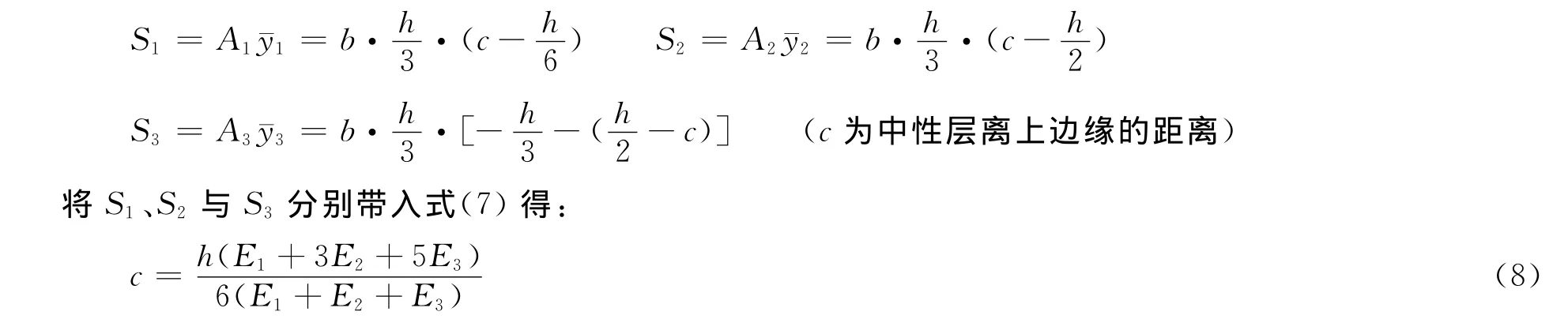
1．3 弯曲正应力计算公式的推导

式中，I1、I2、I3分别为截面A1、A2、A3对中性轴Z的惯性矩。

将式（9）代入式（3），即可得到3层胶结复合梁的正应力分布公式：

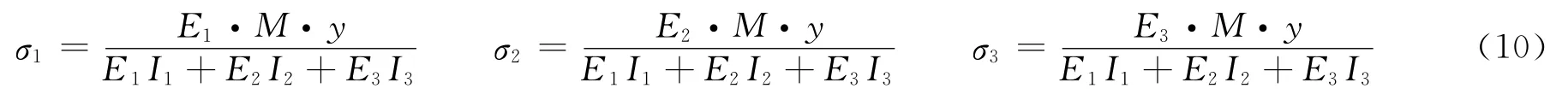
2 测试

测试时所使用的胶结复合梁为自制等截面铝-铝-铝胶结复合梁，在承受纯弯曲变形的前提下，对梁上分布的各点的应变进行测试。胶结复合梁试验装置图如图3所示。载荷P通过双挂环直接加在离支撑点距离为a的位置上。已知铝的弹性模量E=7×105MPa，梁的总长L=600mm，a=125mm，梁厚b=18mm，高h=45mm，据式（8）可以计算出中性层离梁上边缘的距离为22．5mm。

2．1 选点

根据上述理论分析，在纯弯曲梁部分沿着梁横截面高度选15个点进行测试（胶合层除外），从上到下分别标记为1、2、3、4、5、6、7、8、9、10、11、12、13、14、15（见图3）。由于纯弯曲梁部分的各点为单向应力状态，故选择BX120-4AA的应变片即可，应变片的电阻值120Ω·m，灵敏系数2．08。在各测点沿平行于中性层的方向粘帖应变片［3］，然后将应变片的引出线与导线焊接。放置24h并进行防潮处理后，即可进行测试。

图3 胶结复合梁试验装置图

2．2 测试结果与分析

各测点的应变片与应变仪的连接采用半桥公共温度补偿（也叫1／4桥）的接线方法。温度补偿片应粘贴在与测点相同材料的试块上，然后接在应变仪的公共补偿端。应变仪与应变片的灵敏系数应保持一致，这样从应变仪上读取相应电桥的数值即梁上相应位置的应变值，即ε读=ε真。先采用等增量法加载来验证数据的线性关系。载荷增量为100N，即从0开始，载荷为0时应变仪调零，以后每加100N后记录各点的应变值，一直加到600N，再以后1级应变减去前1级应变得出应变增量。由于载荷为100N时各点对应的应变增量基本相等，说明各测点数据线性很好。但考虑应变值太小不利于比较计算，因而最终采用的载荷为600N时测得的各测点的应变值，测试4遍后计算平均应变，其结果如表1所示。

表1 各测点的实测及平均应变值

将表1中各点平均应变值代入式（2）即可计算各点的实测正应力σ测。再根据式（10）计算各测点的理论正应力σ理，最后计算各测点的相对误差（第8点计算绝对误差）（见表2）。

表2 各测点实测及理论正应力比较

由表2可以看出，第5测点为中性层位置，其σ测=σ理=0，理论计算与实际测试结果完全符合；各测点相对误差均在17%以内，基本符合预期结果。

根据表2绘制的实测-理论正应力对比柱状图如图4所示。从图4可以看出，整根梁的正应力分布呈线性，这与理论计算结果相符合，说明胶结复合梁纯弯曲部分的应力分布沿着共同的中性层呈线性分布。同时，实测时的3层胶结复合梁采用同种材料的铝梁，试验结果显示胶结层附近未发生应力跳跃，因而在理论计算时，对于同种材料的胶结复合梁，可以作为一根整梁进行计算。