基于量子蛙跳算法和对传神经网络的油井故障诊断

袁和平 （中石油大庆油田有限责任公司第五采油厂，黑龙江 大庆163513）

机械举升采油方式是目前最主要的、也是应用最为广泛的采油方式。在机械举升工艺中，抽油机-深井泵采油是应用井数最多的举升工艺，简称为抽油机采油方式。由于抽油机井多数安装在野外且工作环境复杂，因此及时准确地掌握采油系统的工作状况，对提高原油采收率、降低能源消耗都有着重要意义。对传神经网络 （Counter Propagation Network，CPN）是一个异构网，2层神经网络执行不同的训练算法，网络的异构性更接近于对人脑功能的模拟，具有较高的学习效率和自适应能力，在模式识别、信号加强等领域具有重要的应用，笔者对传统CPN竞争层神经元的信息处理机制进行改进，充分发挥竞争层的作用，并提出一种量子蛙跳算法来训练网络，在增强CPN网络利用率的同时，提高网络收敛速度和识别精度，采用油井示功图作为网络输入判别油井故障，取得了很好的识别效果。

1 对传神经网络模型

对传神经网络的训练速度比BP网络要快很多，具有潜在的提取输入向量统计特性的能力［1-2］，网络结构如图1所示。其中，输入向量X= （x1，x2，…，xn）；输出向量Y=（y1，y2，…，ym）；Wij表示输入层节点i到竞争层节点j的连接权值向量；Vjk表示竞争层节点j到输出层节点k的连接权值向量。输入层与竞争层执行Kohonen提出的自组织映射算法，完成对Wij的训练和对输入样本的自适应模式分类；竞争层与输出层执行Grossberg提出的散射星算法，完成对Vjk的调整，并输出结果。

在传统CPN竞争层学习算法中，通过：

Dj= ‖Xk-Wj‖j=1，…，Nk=1，…，n

计算输入向量Xk和连接权值Wj的欧几里德距离Dj来比较竞争层中各神经元节点的距离，最小者为获胜者，然后修正那些与获胜神经元j相连的各连接权值，而其他权值保持不变，如果获胜神经元j是Xi的恰当分类，则将相应神经元对应的连接权值向Xi靠拢的方向调整。其权值修正公式为：

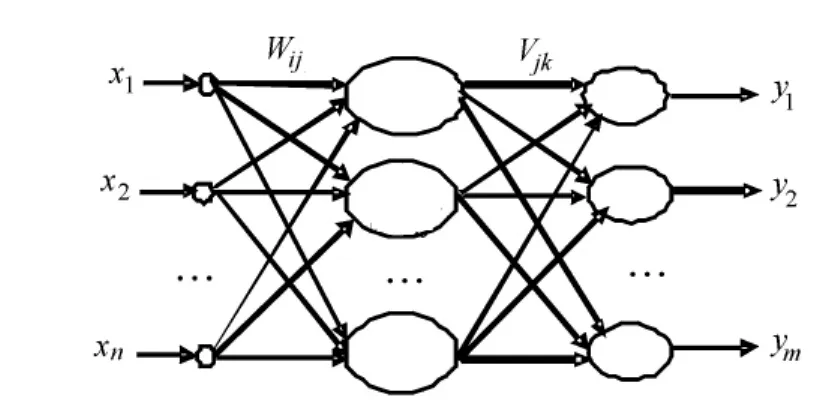
图1 对传神经网络模型

由于只有一个竞争层节点输出为1，其他为0，所以CPN的实际输出Y=V。因此，只针对获胜神经元进行权值调整，其他竞争层神经元保持不变，这使竞争层中存在大量闲置神经元没有发挥作用，造成训练时竞争层的收敛速度较慢，并且初始权值的选取和训练样本的输入顺序对网络训练影响也较大。笔者采用软竞争［3］机制充分发挥竞争层所有神经元的作用，改变它们的信息处理机制，使竞争层神经元对输入的任意样本的输出都不为0，以便输入层到竞争层、竞争层到输出层的神经元节点间的连接权值信息都能发挥作用，进而增强了网络表示能力，因此更改竞争层输出的计算公式：

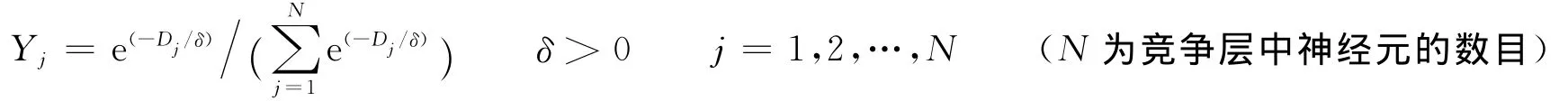
当δ趋于无穷大时就退变为普通CPN；竞争层节点的输出在 （0，1）之间，竞争力较强的节点输出值较大，竞争力较弱的节点输出值相对较小，但竞争层中每个节点对系统都有贡献。由此可得系统实际输出公式Z′=YV，系统误差公式E=∑（Z-Z′）2，由此可知系统待优化参数为Wij和Vjk，传统训练方法对初始值较敏感，当竞争节点增多时会增加训练次数，同时训练样本的次序对算法的收敛也会有一定影响。为提高网络训练速度和识别精度，笔者结合量子计算的高效性和蛙跳算法易于实现和较强的全局寻优能力的特点，提出一种量子蛙跳算法来训练网络结构。

2 量子蛙跳算法

基本蛙跳算法 （Quantum Frog Leaping Algorithm，QFLA）的基本思想［4］是将N只青蛙按适应值进行排序，然后将整个种群分成m个子群，每一个子群里包含n只青蛙（N=mn），对于每个青蛙子群，查找适应值最好的青蛙xb和最坏的青蛙xw，将目前整个青蛙种群中适应值最好的青蛙定义为xg，在每次算法迭代中按照如下公式对最坏青蛙的位置进行调整：

式中，rand是（0，1）之间的随机数；Smax是允许青蛙移动的最大范围。

如果以上操作能产生更好的解，用该解取代原先适应值最坏的青蛙，否则，将xb替换成xg，继续使用式 （1）和式 （2）产生新解。如果该新解较最差解仍无提高，则随机产生一个新解取代原先适应值最坏的青蛙。

2．1 量子蛙跳算法编码方案

量子进化算法［5］是新近发展起来的一种概率进化算法，可以利用较小的群体规模获得更好的群体多样性和全局寻优能力，并且不影响算法性能。在量子计算中，量子比特的状态可用｜φ〉=cosθ｜0〉＋sinθ｜1〉表示，其中，［cos（θ），sin（θ）］T称为量子比特的概率幅，θ是量子比特的相位。在量子蛙跳算法中用概率福作为个体编码，编码方案如下：

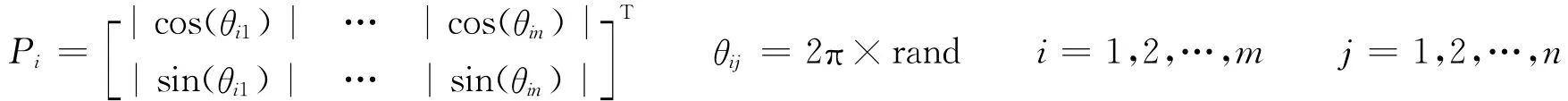
式中，m是种群规模，是解空间维数。可见个体青蛙解空间的每一维均为［-1，1］，因此要计算比较个体目前位置的优劣，需要进行解空间变换：

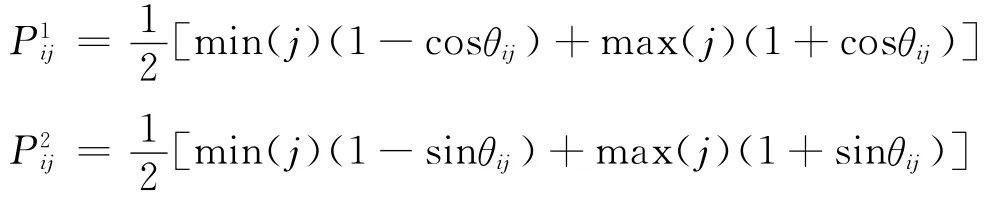
因此，网络结构待优化参数Wij和Vjk可依此进行编码，每个参数都有2种编码方式，增加了解空间的多样性。

2．2 量子蛙跳算法个体更新

设θb为子群最佳幅角，θw为子群最差幅角，θg为种群最佳幅角。

1）子群最差个体量子位幅角增量的更新：

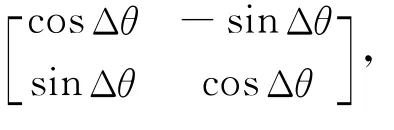
基于量子旋转门的量子位概率幅更新公式为：

如果以上操作能产生更好的解，用该解取代原先适应值最坏的青蛙，否则，将θb替换成θg，继续使用式 （3）和式 （4）产生新解。如果该新解较最差解仍无提高，则随机产生一个新解取代原先适应值最坏的青蛙。

2．3 量子蛙跳算法个体变异

为了增加种群多样性，避免早熟收敛，在量子蛙跳算法中利用量子非门实现个体变异操作。首先确定算法的个体变异概率，然后为每只青蛙产生一个 （0，1）之间的随机数rand，若rand＜p，则用量子非门实现变异：

3 模式分类数的确定

在对传神经网络结构设计中，竞争层节点数选择是个关键问题，笔者给出一种模式分类方法。设实际问题域中包含M个样本，这M个样本已包含了实际问题的所有模式。设定3个聚类参数：初始分类数N0、相似系数阈值θ（假设相似系数越大越相似）和类间距离阈值R，以相似系数的倒数为2个输入样本间的距离，以2类中两两输入样本间距离的最小值为类间距离，分类步骤如下：

步1 在输入样本集中，选取N0（N0≤M）个样本作为N0个模式类的代表，并就此构成N0个类。

步2 将输入样本集中其余样本依次逐个计算与每个已有的模式类代表之间的相似系数。若其中最大的相似系数小于θ，则就以该样本作为成员形成一个新类，并以该样本作为该新类的模式类代表；若其中最大的相似系数大于θ，则将该样本归于相似系数最大的那一类，并以该样本与原类的代表样本的均值作为合并后得新类的代表。

步3 计算N0个类两两之间的类距离。若2个类的类间距离小于R，则将这2个类合并，以2类类代表样本的均值作为新类的代表；若类间距离大于R，则2个样本类不做改变。

步4 执行步3后，分类的个数可能改变，以新的分类个数替代N0。如果分类结果改变，则返回步3继续执行；如果分类结果不再变化，则分类完成，N0即可作为对传神经网络竞争层的参考节点数。

4 仿真试验

4．1 数据处理

采油系统的运动特性和动力特性是分析设备工作状况的重要依据，运动特性是指抽油机悬点运动规律，包括位移、速度和加速度等；动力特性是指悬点所受的载荷，包括惯性载荷、震动载荷、摩擦载荷等，而示功图是由载荷随位移的变化关系曲线所构成的封闭曲线图［6］。因此选用油井示功图实测数据作为故障诊断依据，为精确描述示功图所包含的故障信息，选取油井一个工作周期内400个载荷和位移数据作为样本数据，利用文献 ［7］的方法构造出特征向量，经归一化后作为对传神经网络的输入。

4．2 试验结果

选取采油厂300口不同油井参数和抽油机型号的油井的载荷与位移实测数据作为试验样本。将故障类型大致可分为正常、油井结蜡、抽油杆断脱、固定凡尔漏失、游动凡尔漏失和碰泵等10个类别。其中240口油井数据作为对传神经网络的训练样本，用剩下的60口油井数据作为测试样本。网络结构及参数选择如下：16个输入节点，竞争层10个神经元节点，1个输出节点。误差精度ε=0．001；最大学习次数M=5000，利用量子蛙跳算法训练网络1385次后收敛，部分诊断结果见表1。表2是基于BP神经网络、普通CPN神经网络、QFLA-CPN神经网络的故障诊断结果对比。

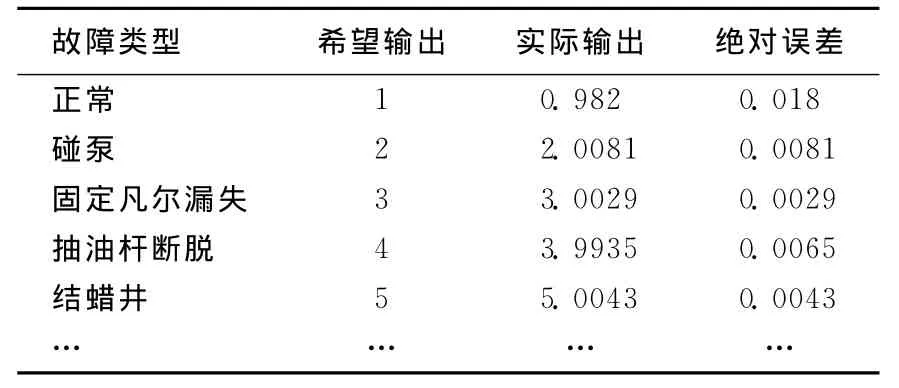
表1 油井故障诊断部分结果表

表1和表2结果表明，量子蛙跳算法由于采用双概率幅编码机制，使得每个青蛙对应于解空间的2个解，这就大大增加了寻找最优解的机会，具有较强的搜索能力和寻优效率，用其训练对传神经元网络具有收敛速度快、识别精度高的优点，这也表明应用量子蛙跳算法和对传神经元网络对油井故障进行诊断是很合适的。

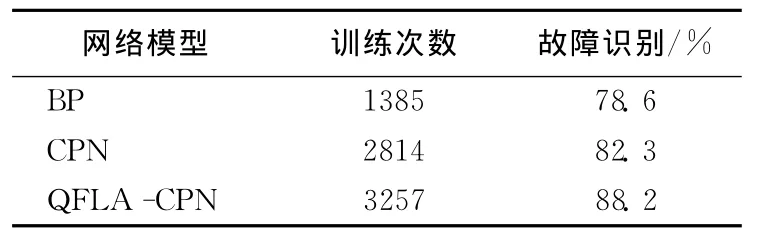
表2 BP、CPN、QLFA-CPN诊断结果对比

［1］Grosberg S．Neural Networks and Natural Intelligence ［M］．MIT Press：Cambridge，MA，1988．

［2］宋晓华，李彦斌，韩金山，等 ．对传神经网络算法的改进及其应用 ［J］．中南大学学报 （自然科学版），2008，39（5）：1059-1063．

［3］郝玉，叶世伟 ．基于软竞争机制的对传网络模型及应用 ［J］．计算机仿真，2006，23（3）：141-144．

［4］Eusuff M M，Lansey K E．Optimization of water distribution network design using the shuffled frog leaping algorithm ［J］．J of Water Resources Planning and Management，2003，129 （3）：210-225．

［5］Hun K H，Kim J H．Quantum-Inspired Evolutionary Algorithm for a Class of Combznatorial Optimization ［J］．IEEE Transon Evolutionary Computing，2002，6 （6）：580-593．

［6］张乃禄，孙换春，郭永宏，等 ．基于示功图的油井工况智能分析 ［J］．油气田地面工程，2011，30（4）：7-9．

［7］刘丽杰，戴庆 ．基于小波包变换和神经网络的油井故障诊断方法 ［J］．长江大学学报 （自然科学版），2008，6（4）：89-91．