一种源顶点到其他各顶点所有路径的算法及其Web服务设计

赵福生 （泉州师范学院数学与计算机科学学院，福建 泉州362000）

现实生活中，常常会碰到如下问题：某个城市的一个大公司在物流配送时，需要把货物运送到全国的各个城市，如何选择配送路径，才能使得总的物流费用最小。解决这个实际问题所需要的决策参考信息是无向网中一个源顶点到其他各顶点的所有路径。

目前，可以利用Dijkstra算法、Bellman-Ford算法和SPFA算法［1］求一个源顶点到其他各顶点的最短路径问题；利用Floyd算法［1］求每对顶点间的最短路径问题。求图中每对顶点间的所有最短路径，况超提出了3种算法：第1种算法是求图中每对顶点间的所有最短路径的基本算法，该算法适用于有向网与无向网，该算法通过逐步加入每条边，并且同时判断加入边以后，每对顶点间的最短路径是否有变化，若有变化，修改相应的最短路径，同时保存相应的直接邻接顶点的编号，最后通过最短路径上直接邻接顶点的编号生成每对顶点间的所有最短路径；第2种算法是求图中每对顶点间的所有最短路径的改进算法，该算法只适用于有向网。该算法先把出度为0的顶点入队列，接下来得到一个出队顶点，找到出队顶点的一个逆邻接顶点，把逆邻接顶点的出度减1，如果逆邻接顶点的出度为0，把逆邻接顶点入队列，同时判断逆邻接顶点到其他各顶点的最短路径是否有变化。若有变化，保存最短路径与直接邻接顶点的编号，对于出队顶点的每个逆邻接顶点都进行上述操作与判断，对于每个出度为0的顶点也都要进行上述操作，最后根据最短路径上直接邻接顶点的编号生成每对顶点间的所有最短路径；第3种算法是求图中受顶点数限制的每对顶点间的所有最短路径的算法，该算法也是按照第2种算法求解最短路径，找到的最短路径上的顶点个数必须满足给定的限制条件［2］。

求有向图中源点到各结点所有路径，毛红梅与甘晟科提出了一种实用算法。该算法在求解源点到当前结点的所有路径以前，必须求出源点到当前结点的所有逆邻接顶点的所有路径，该算法采用拓扑顺序求各个所有路径［3］。但该算法有一个不足的地方，只能求出有向图中源点到各结点所有路径。为此，笔者提出了求解一个源顶点到其他各顶点所有路径问题的一种算法。

1 无向网

用圆圈表示城市，圆圈里面的数字为城市的编号。如果2个城市之间有路线可以到达的话，在2个顶点之间加上一条无向边，无向边上的数值为2个城市之间的距离。按照上述方法构造的图为无向网。图1所示为无向网的一个例子。

图1 无向网的一个例子

2 源顶点到其他各顶点所有路径计算的算法设计

2．1 算法采用的数据结构

1）二维数组 图1所示的无向网采用图2所示的二维数组a来存放。二维数组a的C＃定义如下：

const int INF=1000000000；int［，］a=new int［VertexNumber，VertexNumber］；

其中，INF为符号常量，它的值为1000000000，VertexNumber为一个变量，里面的值为无向网的顶点个数。顶点0到顶点0的距离为0，a［0，0］存放0；顶点0到顶点1有直接路线相连距离为6，a［0，1］存放6；顶点0到顶点2有直接路线相连距离为5，a［0，2］存放5；……；顶点0到顶点5没有直接路线相连，a［0，5］存放INF；顶点1到顶点0有直接路线相连距离为6，a［1，0］存放6；……

2）一维指针数组 源顶点到其他各顶点的所有路径存放在图3的结构中。L为一个一维指针数组，C＃定义如下：

其中，L［0］存放源顶点3到顶点0的所有路径，L［1］存放源顶点3到顶点1的所有路径，L［2］存放源顶点3到顶点2的所有路径，L［4］存放源顶点3到顶点4的所有路径，L［5］存放源顶点3到顶点5的所有路径。L［1］里面的指针指向一个二维链表，二维链表的每个AllPathNode结点存放一条源顶点3到顶点1的路径，AllPathNode结点的edgenumber成员存放路径上的边数，AllPathNode结点的distance成员存放路径上的权值之和，AllPathNode结点的path成员指向一个一维链表，该一维链表存放路径上的各个顶点的编号，顶点的编号存放在一维链表PathNode结点的vertex成员里面，AllPathNode结点的next成员指向下一个AllPathNode结点，二维链表里面的所有路径按照路径上的权值之和从小到大进行存放。

3）路径树 在查找所有路径的过程中，需要建立一棵路径树，路径树中每个结点的结构如图4所示，C＃定义如下：

class TreeNode ｛public TreeNode firstchild；public int level；public int value；public int distance；public TreeNode parent；public TreeNode nextsibling；｝

其中，TreeNode结点的value成员存放当前顶点的编号；Tree-Node结点的distance成员存放源顶点到当前顶点的路径上的权值之和；TreeNode结点的level成员存放源顶点到当前顶点的路径上的边的数目；TreeNode结点的firstchild成员指向当前结点的第一个孩子结点；TreeNode结点的parent成员指向当前结点的父亲结点；Tree-Node结点的nextsibling成员指向当前结点的下一个兄弟结点。

2．2 算法设计

该算法利用路径树来查找源顶点到其他各顶点的所有路径。源顶点3为路径树的根结点 （路径树的第0层），把源顶点3的所有邻接顶点 （顶点0、顶点1、顶点2、顶点4）按照顶点编号的顺序依次作为源顶点3的孩子结点，这是路径树的第1层，同时把路径3-0加入到L［0］里面合适的位置，把路径3-1加入到L［1］里面合适的位置，把路径3-2加入到L［2］里面合适的位置，把路径3-4加入到L［4］里面合适的位置。

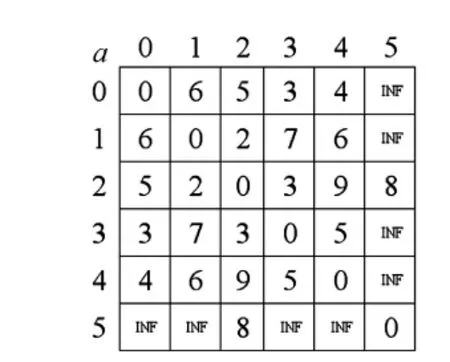
图2 无向网的存储结构

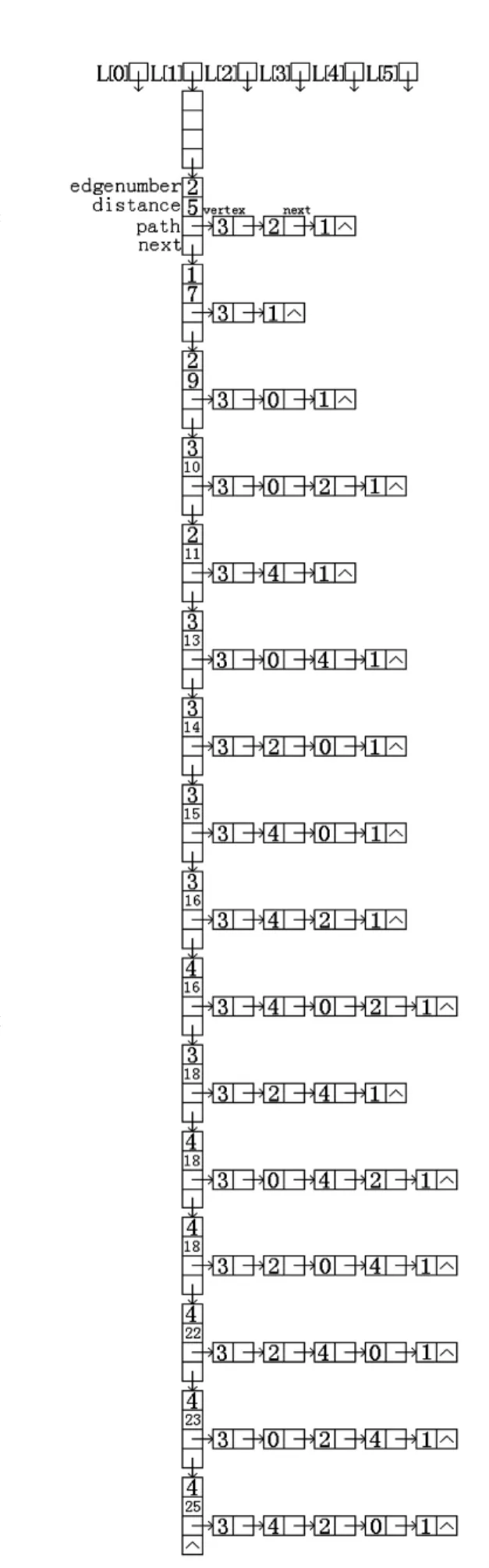
图3 存放所有路径的存储结构

依次把第1层的各个顶点 （顶点0、顶点1、顶点2、顶点4）作为当前顶点，查找当前顶点的没有在源顶点3到当前顶点的路径中的所有邻接顶点，把这些邻接顶点按照顶点编号的顺序依次作为当前顶点的孩子结点，这是路径树的第2层，同时把源顶点3到第2层顶点k的各个路径加入到L［k］里面合适的位置，比如路径3-0-1加入到L［1］里面合适的位置，路径3-0-2加入到L［2］里面合适的位置，路径3-0-4加入到L［4］里面合适的位置，路径3-1-0加入到L［0］里面合适的位置，路径3-1-2加入到L［2］里面合适的位置，路径3-1-4加入到L［4］里面合适的位置，路径3-2-0加入到L［0］里面合适的位置，路径3-2-1加入到L［1］里面合适的位置，路径3-2-4加入到L［4］里面合适的位置，路径3-2-5加入到L［5］里面合适的位置，路径3-4-0加入到L［0］里面合适的位置，路径3-4-1加入到L［1］里面合适的位置，路径3-4-2加入到L［2］里面合适的位置。

图4 路径树中每个结点的结构

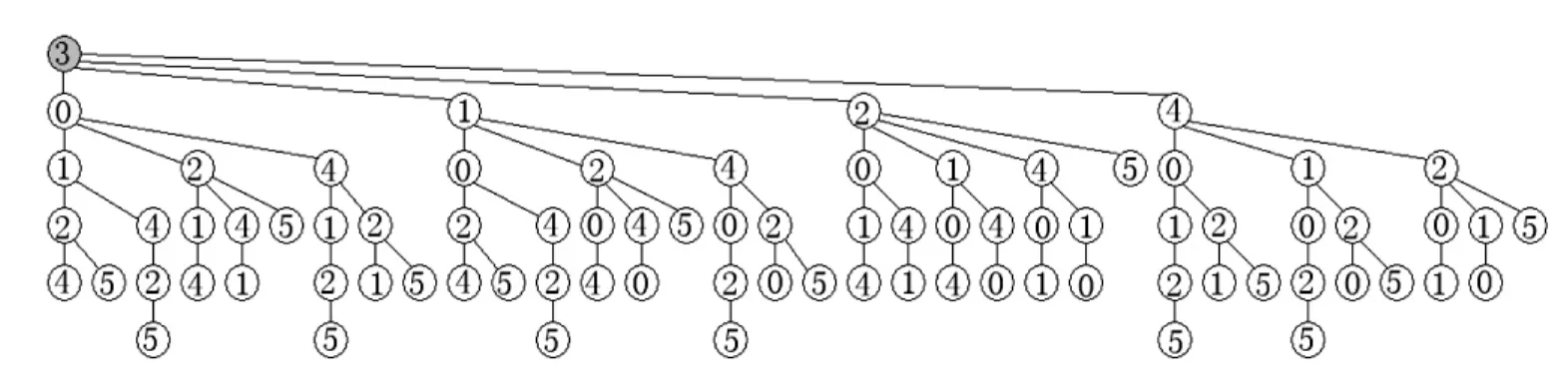
图5 从源顶点3出发的路径树

依次把第2层的各个顶点作为当前顶点，进行上述操作。按照上述方法从上到下从左到右构造的路径树如图5所示。路径树构造完以后，L［k］里面存放源顶点3到顶点k的所有路径，而且，这些所有路径在L［k］里面按照权值之和从小到大进行存放。

3 所有路径Web服务的设计

Web服务是通过后缀为．asmx的文件来提供的，．asmx文件里面的Web方法 ［WebMethod］public string ［］GraphAllPathFromOneVertexToAllVertex （int VertexNumber，string StringOfEdges，int SourceVertex）用来完成所有路径的计算。

public string ［］GraphAllPathFromOneVertexToAllVertex （int VertexNumber，string StringOfEdges，int SourceVertex）

｛／／形参VertexNumber里面的值为顶点个数，形参StringOfEdges里面的值为边的信息，形参SourceVertex里面的值为源顶点的编号。

其中k=FirstAdjacentVertex （VertexNumber，a，p．value）函数用来求p．value的第一个邻接顶点；k=NextAdjacentVertex （VertexNumber，a，p．value，k）函数用来求p．value的相对于邻接顶点k的下一个邻接顶点；TreepContaink（T，p，k）函数用来判断树根结点到p指向结点路径中是否存在顶点k，存在，返回值true；不存在，返回值false；AddPath（T，r，L［k］，a）；函数用来把树根结点到r指向结点这一条路径加入到L［k］指向的二维链表合适的位置。

4 Web服务的调试

针对图1的无向网，Web服务调试时，VertexNumber文本框用来输入顶点的个数 （6），String OfEdges文本框用来输入顶点之间边上的权值 （0 6 5 3 4INF 6 0 2 7 6INF 5 2 0 3 9 8 3 7 3 0 5INF 4 6 9 5 0INF INF INF 8INF INF 0），SourceVertex文本框用来输入源顶点的编号 （3）。输入完以后，单击 “调用”按钮，可以得到源顶点3到其他各顶点的所有路径如下：

顶点3到顶点0的所有路径为：3：3-0、8：3-2-0、9：3-4-0、11：3-2-1-0、13：3-1-0、14：3-1-2-0、15：3-2-1-4-0、16：3-2-4-0、17：3-1-4-0、17：3-4-1-0、18：3-4-1-2-0、19：3-4-2-0、22：3-1-2-4-0、22：3-4-2-1-0、24：3-2-4-1-0、27：3-1-4-2-0。

顶点3到顶点1的所有路径为：5：3-2-1、7：3-1、9：3-0-1、10：3-0-2-111：3-4-1、13：3-0-4-1、14：3-2-0-1、15：3-4-0-1、16：3-4-2-1、16：3-4-0-2-1、8：3-2-4-1、18：3-0-4-2-1、18：3-2-0-4-1、22：3-2-4-0-1、23：3-0-2-4-1、25：3-4-2-0-1。

顶点3到顶点2的所有路径为：3：3-2、8：3-0-2、9：3-1-2、11：3-0-1-2、13：3-4-1-2、14：3-4-2、14：3-4-0-2、15：3-0-4-1-2、16：3-0-4-2、17：3-4-0-1-2、18：3-1-0-2、22：3-1-4-2、22：3-1-4-0-2、22：3-4-1-0-2、24：3-0-1-4-2、26：3-1-0-4-2。

顶点3到顶点4的所有路径为：5：3-4、7：3-0-4、11：3-2-1-4、12：3-2-4、12：3-2-0-4、13：3-1-4、15：3-0-1-4、15：3-2-1-0-4、16：3-0-2-1-4、17：3-0-2-4、17：3-1-0-4、18：3-1-2-4、18：3-1-2-0-4、20：3-0-1-2-4、20：3-2-0-1-4、27：3-1-0-2-4。

顶点3到顶点5的所有路径为：11：3-2-5、16：3-0-2-5、17：3-1-2-5、19：3-0-1-2-5、21：3-4-1-2-5、22：3-4-2-5、22：3-4-0-2-5、23：3-0-4-1-2-5、24：3-0-4-2-5、25：3-4-0-1-2-5、26：3-1-0-2-5、30：3-1-4-2-5、30：3-1-4-0-2-5、30：3-4-1-0-2-5、32：3-0-1-4-2-5、34：3-1-0-4-2-5。

由上述求得的源顶点3到其他各顶点的所有路径，可知笔者设计的Web服务是可行和有效的。

5 算法复杂度分析

笔者提出的算法适用于所有的无向网。对于每个无向网，出现的概率不相等，因此，不能求平均情况下的时间复杂度与空间复杂度，只能求最坏情况下的时间复杂度与空间复杂度，从而估算执行时间增长率的一个上界与所需存储空间增长率的一个上界。最坏情况的无向网为：每个顶点到其他顶点都有边。这时，整个算法所需要的时间T（n，m）随问题规模n的增大而增大，增长率与n！大概相同，因此，最坏情况下，该算法的时间复杂度为：

T（n，m）=O（n！） （n为顶点个数；m为边数）

这时，整个算法所需要的存储空间S（n，m）随问题规模n的增大而增大，增长率与n！大概相同，因此，最坏情况下，该算法的空间复杂度为：

S（n，m）=O（n！）

6 结 语

提出了求解一个源顶点到其他各顶点所有路径问题的一种算法，设计所有路径的Web服务，并完成Web服务的调试，运行结果找出了源顶点到其他各顶点的所有路径，验证了该算法的可行性和有效性。

［1］王桂平，王衍，任嘉辰 ．图论算法理论、实现及应用 ［M］．北京：北京大学出版社，2011．

［2］况超 ．求图中每对顶点间的所有最短路径算法的分析与研究 ［D］．上海：华东师范大学，2011．

［3］毛红梅，甘晟科 ．求有向图中源点到各结点所有路径的一种实用算法 ［J］．微电子学与计算机，2009，26（3）：128-130．

［4］孙强，杨宗源 ．求受顶点数限制的最短路径问题的一个算法 ［J］．计算机工程，2002，28（9）：73-74．

［5］王卫强，孙强 ．求图中受顶点数限制的所有最短路径的算法 ［J］．计算机工程与设计，2008，29（7）：1754-1757．

［6］LI Guang-ru，HU Jing-feng，Sun Zhi．Structure and algorithm design of the manager agent in WebGIS ［A］．IEEE Proceedings of the Fifth International Conference on Machine Learning and Cybernetics ［C］ ．Dalian：IEEE Computer Society，2006：40-45．

［7］王泽来 ．基于Web服务集成的物流应急关键技术研究 ［D］．天津：天津大学，2012．