动态规划算法分析

宛 楠 （皖南医学院计算机教研室，安徽 芜湖241000）

张 义 （安徽工程大学计算机与信息学院，安徽 芜湖241000）

ACM国际大学生程序设计竞赛 （简称ACM／ICPC）是由国际计算机界历史悠久、颇具权威性的组织ACM学会 （Association for Computer Machinery）主办，是世界上公认的规模最大、水平最高的国际大学生程序设计竞赛，在信息技术界具有相当的影响力，竞赛的很多题目都是在实际的工程项目应用中遇到的问题，能够比较全面的考察学生对计算机以及其他学科知识的综合运用能力，通过竞赛可以系统的检验学生的计算机编程等方面的综合水平，而这些正是IT从业者所急需的。在竞赛中涉及到各种算法，其中动态规划是较为常见的算法之一［1］。下面，笔者对动态规划算法的进行了分析和研究❶。

1 动态规划算法的基本思想与步骤设计

1）动态规划算法的基本思想 动态规划算法基本思想是将所求解问题分解成若干个子问题，先求解子问题并保存已解决的子问题的答案，然后从这些子问题的解得到原问题的解。

2）动态规划算法步骤设计 动态规划算法适用于解最优化问题，一般可按以下步骤设计动态规划算法：①找出最优解的特质，并描述其结构特征；②用递归的方式定义最优值；③以自下向上的方式计算出最优值；④根据计算最优值时得到的信息，构造最优解。

步骤①～③是动态规划算法的基本步骤。如果只需要求出最优值，则步骤④可以省去。如果从最底层的子问题开始，自底向上地逐一推导出子问题的解，则编程的时候可不写递归函数［2］。

2 数字三角形问题的动态规划算法求解

下面以数字三角形为例，说明动态规划算法的具体实施。

1）数字三角形问题描述 图1给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。对于每条路径，把路径上面的数加起来可以得到一个和，和最大的路径称为最佳路径。问题是求出最佳路径上的数字之和，路径上的每一步只能从一个数走到下一层上和它最近的左边的数或者右边的数［3］。

2）具体实施过程 按照题目的要求，从顶点出发，假设先采用贪心法来求最佳路径，每次选择所能选的最大值作为下一步的路径，则从顶点7出发选择8，从8出发选择1，从1出发选择7，从7出发选择5，所求最终路径为7-8-1-7-5，如图2所示，路径和为28。然而，这个路径并非题目所要求的最优路径，最优路径应该为7-3-8-7-5，如图3所示，路径和为30。可见该问题采用自顶至下的贪心法是不能得到正确答案的。换言之，从顶点出发是无法直接判断是选择左下还是右下的数字。

转换思路，从倒数第2层 （2、7、4、4）出发，则可以立刻做出判断，即从2出发选择5，从7出发选择5，从4出发选择6，4从出发选择6，求和后更新该数字三角形，再从新的三角形的倒数第2层（8、1、0）出发，同样可以立即做出判断，即从8出发选择12，从1出发选择12，从0出发选择10，求和后更新该数字三角形，依次类推直到最顶层，如图4所示，此时该三角形只剩一个顶点，该顶点即为所求的最佳路径和。这个过程就是动态规划算法在求解该问题上的应用。

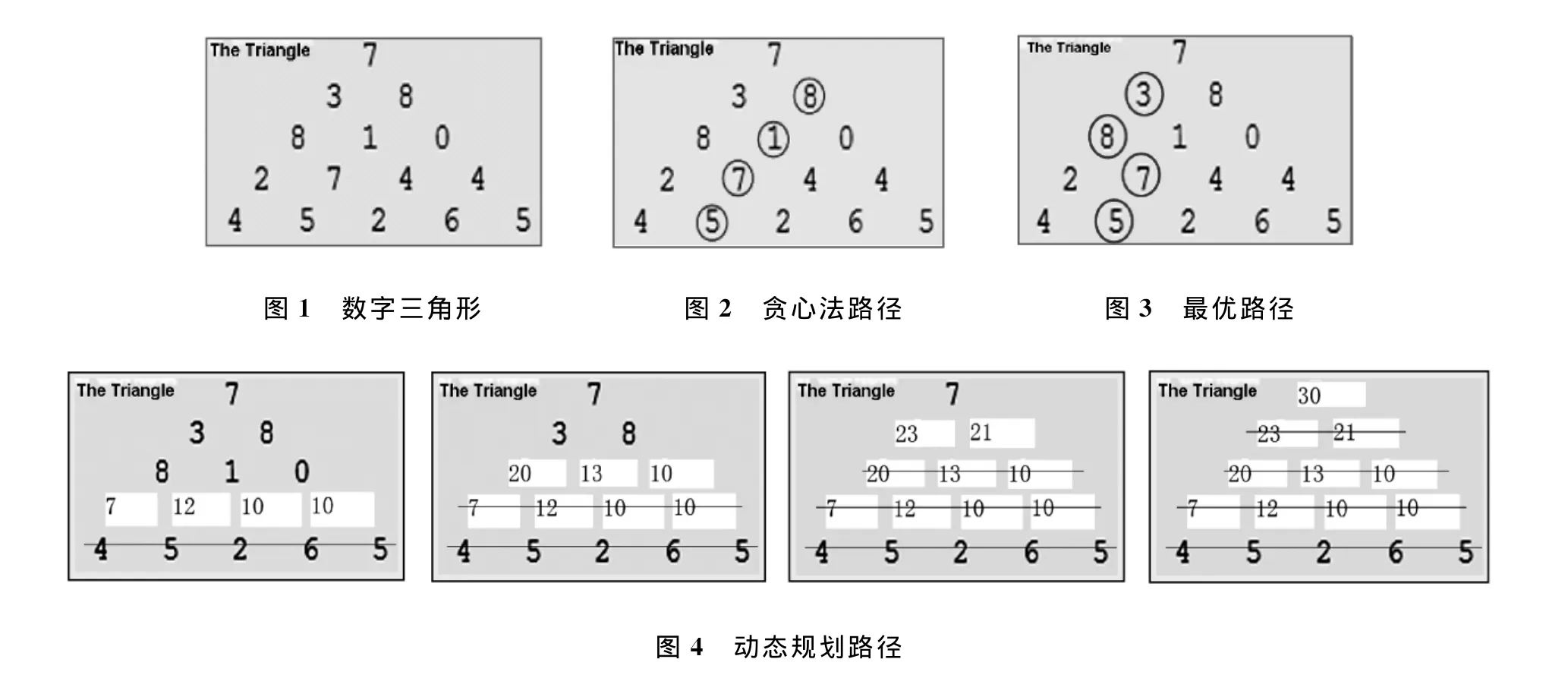
3）算法实现 定义二维数组a来存放数字三角形，二维数组f来存放每次求和后产生的新数字三角形，则a［i，j］表示当前位置的值，f［i，j］表示在i、j这个位置能取得的最大值：

3 动态规划算法解题的一般思路

在用动态规划算法解题时，往往将和子问题相关的各个变量的一组取值称为一个 “状态”。一个状态对应于一个或多个子问题，所谓某个状态下的 “值”，就是这个状态所对应的子问题的解［4］。

具体到数字三角形的例子，子问题就是 “从位于（i，j）数字开始，到底边路径的最大和”。这个子问题和变量i，j相关，那么一个状态就i，j的一组取值，即每个数字的位置就是一个状态。该状态所对应的值，就是从该位置的数字开始，到底边的最佳路径上的数字之和，即源代码中的f［i］［j］。

确定出什么是状态以及在该状态下的值后，就要明确不同的状态之间怎样迁移——即如何从一个或多个值已知的状态，求出另一个状态的值。状态的迁移可以用递推公式表示，该递推公式又称为 “状态转移方程”。如数字三角形中的状态转移方程为：

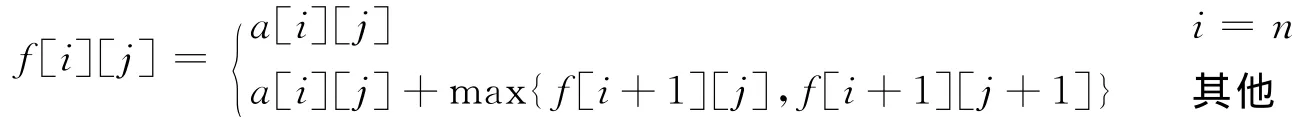
4 结 语

程序设计竞赛是提高大学生综合素质的一个很好的平台，在参赛的准备过程中会涉及到各种算法，其中动态规划算法是最为常见的一种。笔者通过数字三角形详细说明了动态规划算法的解题过程，并给出了动态规划算法解题一般思路，用动态规划算法解题，应该如何寻找子问题、定义状态、状态转移方程是什么样的，都需要具体问题具体分析。当然，笔者给出的例子属简单动态规划，更为复杂的动态规划算法如双重动态规划，还需进一步探讨。

［1］王宏，吴文虎 ．清华实践教学 “赛课结合”新思路 ［J］．计算机教育，2006（7）：12-14．

［2］刘汝佳 ．算法竞赛入门 ［M］．北京：清华大学出版社，2009：158-159．

［3］李文新，郭炜，余华山 ．程序设计导引与在线实践 ［M］．北京：清华大学出版社，2007：221-226．

［4］王晓东 ．算法设计与分析 ［M］．第2版 ．北京：清华大学出版社，2008：61-62．