曲率半径变化对高墩大跨连续刚构桥静力性能的影响*
2013-01-04颜浩杰束景晓
陈 淮,颜浩杰,李 杰,束景晓
(1.郑州大学土木工程学院,河南 郑州450001;2.河南省交通运输厅高速公路管理局,河南郑州450003)
随着我国高速公路的大规模建设,在中西部山区建造了多座高墩大跨径预应力混凝土连续刚构桥。受桥址处的地形、地貌的影响,或道路线形走向的限制,很多高墩大跨径连续刚构桥设置在曲线上。预应力混凝土连续刚构桥目前主要采用悬臂浇筑法施工,连续刚构桥施工时,桥梁不仅要经历T型刚构阶段形成主梁的过程,还要经历体系转换的过程,桥梁经历了复杂的受力过程[1]。因此,对于采用悬浇施工的高墩大跨径预应力混凝土曲线连续刚构桥,为了确保桥梁施工安全和保证施工质量,需要对其进行施工过程和成桥状态的受力分析[2-7],全面了解桥梁的静力力学性能。本文以某高墩大跨径预应力混凝土曲线连续刚构桥为研究背景,分别建立直线刚构桥和不同曲率半径的曲线刚构桥有限元计算模型,进行桥梁悬臂施工过程及成桥运营阶段的数值仿真分析,研究桥梁在最大悬臂阶段和成桥阶段下曲率半径对桥梁内力和变形的影响,了解结构受力及变形特点,总结曲率半径变化对高墩大跨径预应力混凝土连续刚构桥静力力学性能的影响规律。
1 工程简介
以河南省西部山区某高速公路在建的一座大跨径曲线双薄壁高墩预应力混凝土连续刚构桥为研究对象。该桥主跨170 m,跨径组成(95+170+95)m。全桥上下行分离,采用两幅桥梁,每幅主梁采用单箱单室变高度预应力混凝土箱梁,箱梁顶宽12.2m,底宽 6.5m;箱梁根部梁高 10.5m,跨中梁高3.6m,箱梁高度按1.8次抛物线变化;上部结构按全预应力混凝土结构设计,采用纵、横、竖三向预应力体系。主墩为矩形截面空心薄壁墩,墩高分别为62 m和68 m。该桥采用悬臂浇筑法施工,先进行下部结构施工,施工完成0号块节段后再对称向两侧悬臂施工,形成单“T”型刚构,先合拢边跨,再合拢中跨,完成桥梁上部结构施工。主梁施工时最大悬臂长度84m,其中0号块节段长16 m,每个悬浇“T”型刚构纵向对称划分为21个节段,节段悬浇总长76 m,边、中跨合拢段长均为2 m,边跨现浇段长8.94 m,在桥台旁搭设支架现浇施工。该桥梁立面图见图1。
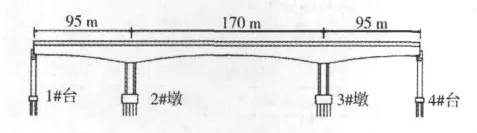
图1 主桥立面图Fig.1 Elevations plan of main bridge
2 有限元建模
采用MIDAS/Civil有限元软件进行计算,主梁采用变截面空间梁单元模拟,主墩采用一般空间梁单元模拟,预应力束采用施加预应力荷载模拟;施工过程中节段湿重、挂篮重量采用节点力和节点弯矩模拟;计算模型中按照规范规定考虑混凝土收缩、徐变效应和混凝土强度随时间增长效应。计算模型的边界条件为连续刚构桥的墩底采用固结模拟,墩梁采用弹性连接中的刚性连接实现;对于曲线刚构桥模型,分别定义桥台处支座节点的局部坐标轴,从而约束该节点的顺桥向位移和横桥向位移。采用满堂支架施工边跨现浇段时,根据连续梁的约束形式对现浇段进行约束,即约束1个节点的竖向和纵向位移,其余节点仅约束竖向位移。体系转换后,边跨现浇段支座处按照设计图纸支座情况模拟双支座,分别约束支座处节点的竖向位移和横向位移,其它节点约束释放;其中支座处节点和主梁节点采用主从节点连接,主梁节点为主节点。单幅桥梁共划分187个节点,182个单元,计算模型如图2所示。
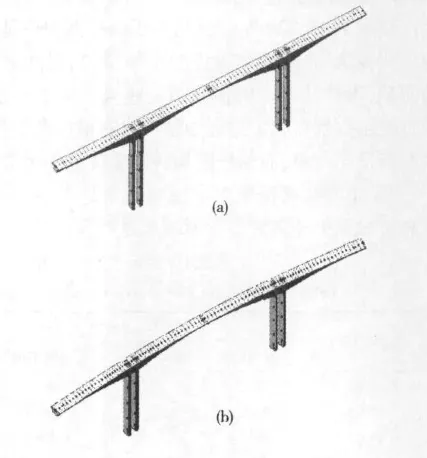
图2 桥梁有限元计算模型Fig.2 Finite element model of bridge structure
3 曲率半径对桥梁静力力学性能的影响
分别建立该桥梁的直线刚构桥计算模型和圆曲线半径分别为1.5 km,2 km和2.5 km的曲线刚构桥计算模型,对比分析直线刚构桥和曲线刚构桥在最大悬臂阶段和成桥状态下的静力力学性能。内力方向如图3所示,其中坐标轴为单元局部坐标轴,图示方向为内力正方向。
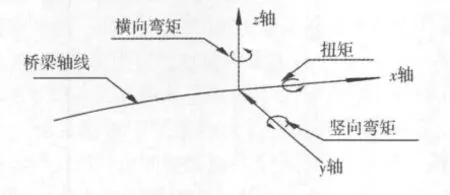
图3 内力方向示意图Fig.3 Internal force direction
3.1 横向弯矩、扭矩
以圆曲线半径为2 km的曲线刚构桥为例,通过计算可以得出,主梁横向弯矩、扭矩主要由恒荷载(包括结构自重与施工阶段的临时施工荷载)与预应力钢束共同作用产生,其中,恒荷载作用最大,主梁横向弯矩和扭矩的最大值出现在墩顶两侧。直线刚构桥和不同曲率半径的曲线刚构桥主梁根部横向弯矩及弯矩计算结果见表1。
由表1可以看出:直线刚构桥的主梁无横向弯矩,但曲线刚构桥随着曲率半径的减小主梁根部最大横向弯矩逐渐呈增大趋势,且增加幅度显著,最大增幅量为33.326%。这是由于曲线刚构桥是空间变化的结构,故曲率半径越小桥梁,其空间效应越明显,导致其主梁的横向弯矩越大。对于桥墩,因直线刚构桥在施工过程中桥墩没有横桥向偏位,故没有横向弯矩,而曲线刚构桥随着曲率半径的减小,主梁重心偏离桥墩中心距离越来越大,导致主梁和桥墩发生径向弯曲变形越来越严重,故桥墩横向弯矩逐渐增大。对比分析以上4种曲率半径的曲线刚构桥计算结果可以看出,桥墩的横向弯矩增长率较大,最大值达33.325%。
在成桥状态,主梁根部的横向弯矩和桥墩的横向弯矩与最大悬臂状态有相似的规律。直线刚构桥主梁无横向弯矩,曲线刚构桥随着曲率半径的减小主梁根部最大横向弯矩有逐渐增大的趋势,增加幅度显著,最大值为24.963%,桥墩的横向弯矩最大增幅为24.966%。
直线刚构桥和不同曲线半径的曲线刚构桥主梁根部扭矩计算结果如表2所示。
由表2可以看出:主梁根部扭矩数值较大,比竖向弯矩小1个数量级。直线刚构桥主梁无扭矩,曲线刚构桥随着曲率半径的减小,主梁根部最大扭矩逐渐呈增大趋势,增加幅度显著,最大增幅为25%。成桥状态主梁根部最大扭矩随曲率半径的变化规律与最大悬臂状态时的计算结果类似,最大增幅为25%。
3.2 径向位移和扭转角
曲线刚构桥与直线刚构桥相比,会产生径向位移。产生径向变形的主要原因有:(1)由于曲线刚构桥存在曲率,使桥墩侧向受力不平衡,产生弯曲变形;(2)桥墩的柔性较大,例如本桥,桥墩为高度达68 m的薄壁空心墩,在由梁体自重产生的竖向压力和弯矩作用下必然产生较大的变形;(3)桥墩顶墩梁固接,不能产生相对转角,梁体随着桥墩的弯曲变形会产生侧向翻转,从而减小了悬臂端的横向变形,故墩顶横向变形较悬臂端大。直线刚构桥和不同圆曲线半径的曲线刚构桥最大径向变形值如图4和图5所示。

表1 最大悬臂状态时不同曲率半径桥梁主梁根部横向弯矩对比Table 1 Cantilever root transverse moment under the largest cantilever case of different curvature radius kN·m

表2 最大悬臂状态时不同曲率半径桥梁主梁根部扭矩对比Table 2 Cantilever root torsion under the largest cantilever case of different curvature radius kN·m

图4 最大悬臂状态时不同曲率半径桥梁最大径向位移对比Fig.4 The maximum radial displacement under the largest cantilever case of different curvature radius
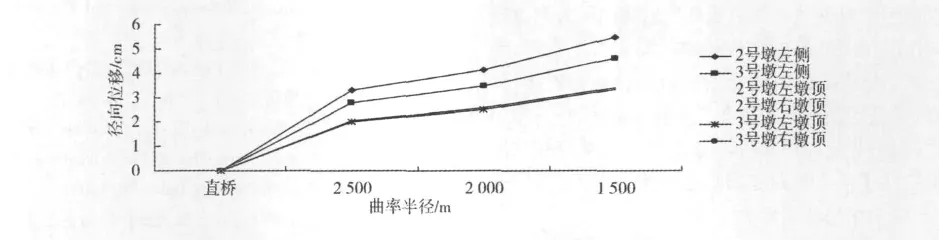
图5 成桥状态时不同曲率半径桥梁最大径向位移对比Fig.5 The maximum radial displacement under fininshed case of different curvature radius
由图4和图5可以看出:随着桥梁曲率半径的减小,桥梁的最大径向变形整体上呈增大趋势,增加幅度较大,最大悬臂状态时最大增幅为25%,成桥状态时最大增幅为24.95%。说明桥梁弯曲程度越大,引起结构的横向变形效应越大。
对于曲线刚构桥,扭转角主要由3部分组成:(1)由主梁自身扭转产生;(2)墩顶处弯曲使悬臂曲梁产生附加扭转角;3)由于几何曲率影响,悬臂曲梁的竖向弯曲也会使梁体产生外侧高内侧低的变形。
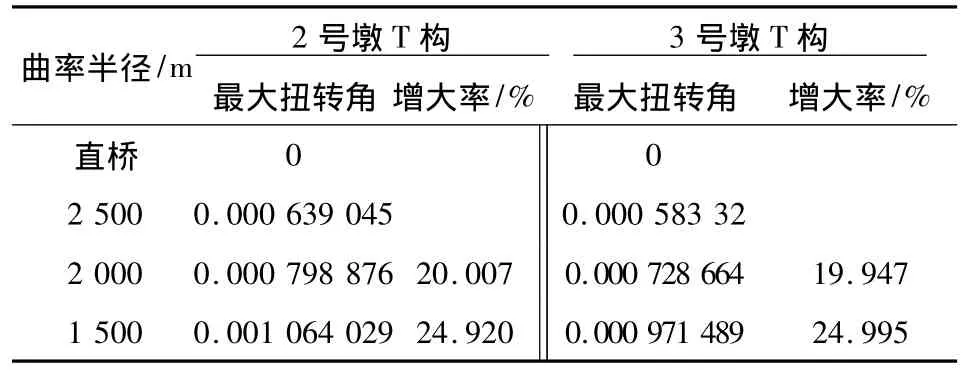
表3 最大悬臂状态时不同曲率桥梁主梁最大扭转角对比 Table 3 Main girder’s maximum torsion angle under the largest cantilever case of different curvature radius rad
由表3和表4可以看出,随着桥梁曲率半径的减小,桥梁最大扭转角整体上呈增大趋势,增加幅度较大,最大悬臂状态最大值约为25%,成桥后在汽车荷载作用下最大值约为426%。说明桥梁弯曲程度越大,引起结构的扭转效应越大,扭转角会使桥面在使用过程中发生一定程度的倾斜,影响行车的舒适性,在桥梁施工时要预防主梁产生扭转角,可考虑预留扭转角预拱度。
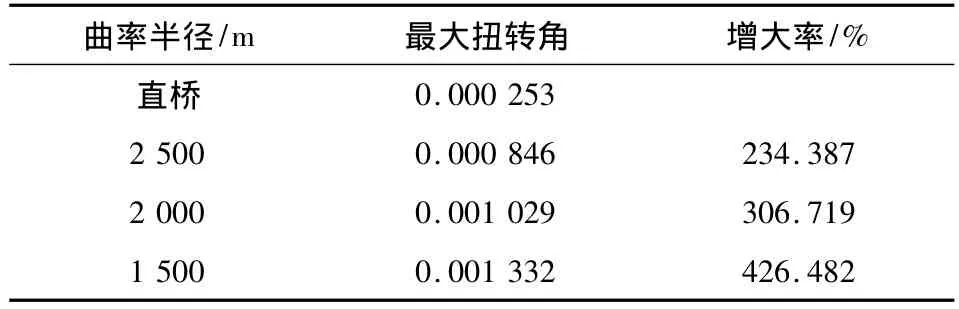
表4 汽车荷载作用下不同曲率桥梁主梁最大扭转角对比Table 4 Main girder’s maximum torsion angle under vehicle load of different curvature radius rad
3.3 竖向弯矩和竖向位移
主梁的最大竖向弯矩和竖向位移随曲率半径的变化比其横向弯矩、扭矩和横向变形、扭转角随曲率半径的变化小。具体计算结果见表5。
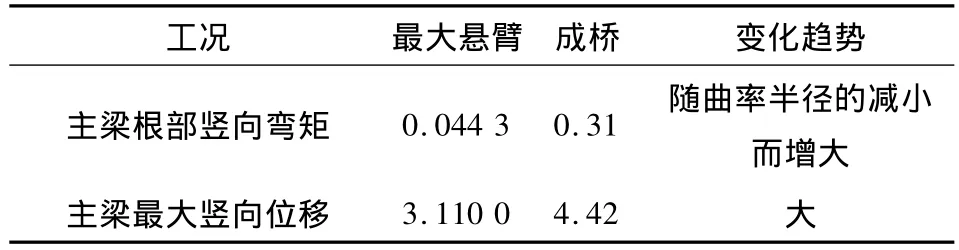
表5 不同曲率半径桥梁主梁竖向弯矩、竖向位移变化规律Table 5 Vertical bending moment and Vertical displacement’s variation law of different curvature radius bridges
由表5可以看出:曲率半径的减小对主梁竖向弯矩和竖向位移影响较小。
4 结论
(1)曲线刚构桥呈现出的复杂受力和变形特点:曲线刚构桥主梁的受力与变形在空间上呈现出“弯扭耦合”的特点,即荷载使主梁产生弯矩的同时,必然耦合产生扭矩,反之亦然。因此,曲线刚构桥主梁产生竖向弯矩和竖向变形,还会产生较大的横向弯矩、扭矩、径向变形和扭转变形,桥墩会产生内倾变形;在曲线梁体自重产生的竖向压力和弯矩作用下,墩身较高的柔性桥墩径向受力不平衡,产生较大的弯曲变形;由于刚构桥墩顶墩梁固接,梁体随着桥墩的弯曲变形会产生侧向翻转,进一步加大主梁的径向变形和扭转变形;由于主梁存在几何曲率,主梁产生竖向变形后还产生一定的扭转,这也构成主梁扭转变形的一部分。
(2)主梁根部的最大横向弯矩、最大扭矩,主梁的径向、扭转变形、桥墩横向弯矩、墩顶最大径向变形均随着桥梁曲率半径减小而显著增大,增大率最大值达24%~33%,桥梁整体结构的受力与变形随着桥梁曲率半径的减小变得更为不利。
(3)为了确保曲线刚构桥成桥后内力和线形满足设计要求,在施工过程中需要预设预拱度;同时应对施工关键控制截面进行应力监控,确保桥梁施工质量和施工安全。
[1]马保林.高墩大跨连续刚构桥[M].北京:人民交通出版社,2001.MA Bao-lin.Long-span high-pier continuous rigid frame bridge[M].Beijing:China Communications Press,2001.
[2]李 杰.大跨径PC连续刚构桥设计参数优化研究[D].西安:长安大学,2003.LI Jie.Analysis of design parameter optimization of long-span PC continuous rigid frame bridge[D].Xi’an:Chang’an University,2003.
[3]齐 林,黄方林,贾承林.连续刚构桥施工线形和应力的分析与控制[J].铁道科学与工程学报,2007,4(2):29-33.QI Lin,HUANG Fang-lin,JIA Cheng-lin.Alignment and stress control for construction of continuous rigid frame bridge[J].Journal of Railway Science and Engineering,2007,4(2):29 -33.
[4]胡雄伟.大跨连续刚构桥主梁设计参数的优化研究[D].昆明:昆明理工大学,2008.HU Xiong-wei.Box- Girder design parameter optimization of long span rigid frame bridge[D].Kunming:Kunming Science and Technology University,2008.
[5]郭 凡,杨永清,贾舒阳.高墩大跨预应力混凝土曲线连续刚构桥内力分析[J].四川建筑科学研究,2009,35(6):35-37.GUO Fan,YANG Yong-qing,JIA Shu-yang.Inner force analysis of curved prestressed concrete rigid frame bridge with long - span and high piers[J].Sichuan Building Science,2009,35(6):35 -37.
[6]杨艳军.曲线连续刚构桥力学性能研究[D].西安:长安大学,2010.YANG Yan-jun.Study on the mechanical properties of the curved rigid frame bridge[D].Xi’an:Chang’an University,2010.
[7]洪新民,钟新谷,沈明燕.PC连续刚构梁桥合拢时机的分析[J].铁道科学与工程学报,2010,7(4):11 -14.HONG Xin-min,ZHONG Xin-gu,SHEN Ming-ya.Analysis on construction closure occasion of PC continuous rigid frame bridge[J].Journal of Railway Science and Engineering,2010,7(4):11 -14.
