基于有限元－边界元无砟轨道声辐射特性分析*

刘林芽，吕 锐，许群峰，邱仕辉

(1．华东交通大学铁路环境振动与噪声教育部工程研究中心，江西南昌330013;2．广州市地下铁道总公司，广东广州510310)

随着中国铁路和城市轨道交通的飞速发展，列车运行的速度不断提高，而由此带来的环境与安全问题也日益突出。其中高速铁路轮轨噪声就严重干扰了人们的正常生活、工作和身体健康［1］。每一种噪声均是由相对应结构的振动所产生，而轮轨噪声产生的原因则是车轮和钢轨之间相互作用产生的振动，随之向外辐射出声波而形成的。轮轨噪声按产生机理可分为三种噪声:滚动噪声、冲击噪声、摩擦噪声。轮轨滚动噪声的产生是［2］因为轨道系统中钢轨表面的短波不平顺激发，当车轮通过此不平顺的钢轨时，车轮将产生振动，振动通过空气传播而产生噪声，产生机理如图1所示。冲击噪声是车轮经过钢轨接缝处或表面呈波纹状的钢轨、车轮辙叉、车轮扁疤所产生的噪声;摩擦噪声也称尖啸声，是当列车通过小半径曲线钢轨时产生的高音调噪声。

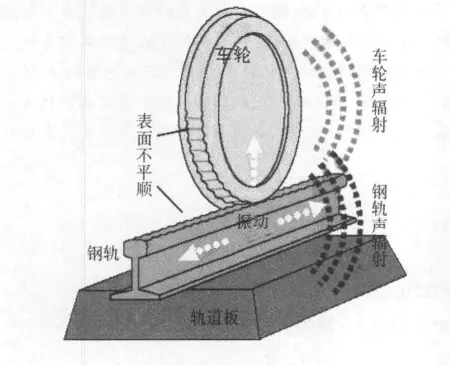
图1 轮轨滚动噪声产生机理及其传播途径Fig．1 The rolling wheel/rail noise generation mechanism and the transmission way

在高速铁路中，轮轨滚动噪声是高速铁路的主要噪声，而滚动噪声实际上就是轮轨之间的高频振动造成的［3］。在轨道系统的声辐射问题上，国外一些学者如Remington［4］从轮轨相互作用角度出发，在轮轨系统动力特性分析的基础上，建立了轮轨滚动噪声预测模型;紧接着Thompson在Remington的基础上建立了轨道声辐射二维模型，他利用有限元法和边界元法，研究了车轮与轨道的声辐射特性［5－6］;Nielsen［7］利用边界元法预测轨枕声辐射。国内学者中，徐志胜［8］运用车辆 －轨道耦合动力学与声辐射理论，建立了基于时域的轨道结构噪声预测模型;吴天行［9］利用有限元法和边界元法研究了钢轨的振动模态及其声辐射特性;方锐［10］结合有限元和边界元方法对在不同轨道结构参数下，轨道结构的声辐射特性;另外，国内还有其他学者［11－13］也对轮轨高频振动与噪声的理论计算进行了大量研究。

文章以高速铁路无砟轨道为研究对象，建立了轨道系统垂向高频振动声辐射计算模型，运用有限元和边界元相结合的方法，将文献［12］计算出轨道系统的垂向高频振动响应作为声辐射计算边界条件，研究线路见图2，最后可以得到钢轨与轨下结构的声辐射特性。

1 轮轨噪声预测直接边界元法

边界元法是在有限元法之后发展起来的一种较精确有效的工程数值分析方法，它与有限元法相比，由于降低了问题的维数，而显著降低了自由度数，所以边界元法被公认为在分析结构声学数值问题中有巨大的优势［14－16］。

对于声学波动方程，由傅里叶变换可知，随时间变化的任意振动都可以看作是多个简谐振动的叠加或积分，可以推导出钢轨声辐射的Helmholtz方程，其微分方程式为:

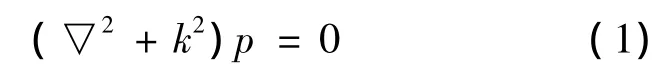
式中:▽2为拉普拉斯算子;为声波波数;c为空气介质中的声速;ω为角频率;p为声压。

针对钢轨辐射外声场，采用直接边界元法，将钢轨结构表面S离散成M个边界单元，其节点数为K，1个单元上的节点数为 L，p′和 v′n表示节点L的声压和法向振速。则钢轨表面单元上任意一点的声压和法向振速可用单元节点的声压和法向振速表示为:

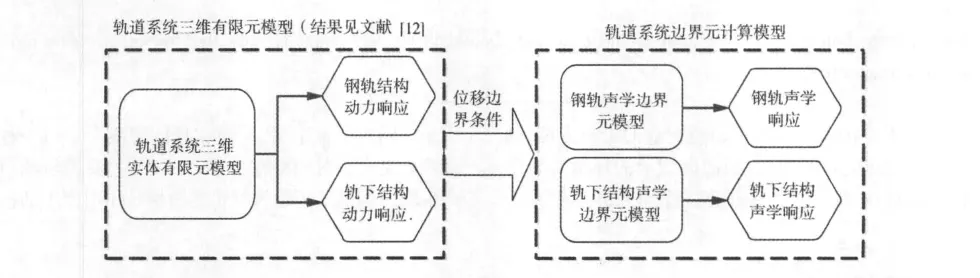
图2 研究线路图Fig．2 The circuit diagram

式中:Nl(ξ，η)为插值函数，依次将每个节点作为源点，即可得直接边界元法的求解方程，其表达式为:

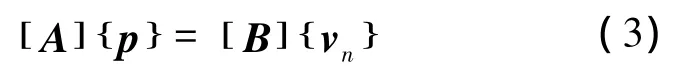
式中:［A］、［B］为K×K阶系数矩阵;{}p 为结构(钢轨)表面节点声压向量;{vn}为结构(钢轨)表面节点法向速度向量。通过求解方程(3)就可以求得钢轨结构表面节点声压向量{p}。

对于空间声场中任意一点r(r∉S)的声压，可由钢轨表面上的声压 {p}和法向振动速度{vn}积分得到:

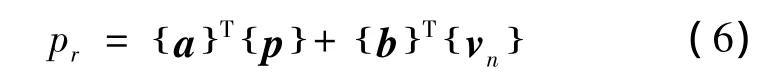
式中:{a}和{b}为插值系数向量。

2 轨道系统边界元计算模型

由于模型结构和边界条件的对称性，在轨道中心设置一个对称面来研究轨道系统的声辐射情况。利用边界元来计算钢轨的噪声辐射量时，边界元网格对最后结果的求解有很大影响，模型选取越长，网格划分的越细，数目越多，计算时对计算机的要求就越高［17］。

采用直接边界元法对轨道系统进行声辐射特性分析，由于混凝土底座对轨道系统声辐射贡献很少，所以，轨下结构只考虑轨道板，重新划分网格并计算满足精度要求后，边界元模型如图3所示。

图3 轨道系统边限元计算模型Fig．3 Transient boundary element model of the rail system

通过轨道系统辐射声场云图可以非常直观地形象地看出轨道系统周围空间声辐射特性的辐射情况与变化情况。为了了解轨道系统的振动声辐射特性，在轨道系统附近位置建立了1个面场点和4个点场点。其中面场点位于轨道系统的左方，与列车运行方向平行，距离钢轨中心线1．0 m，其平行轨道方向长度为5．0 m，高度为2．0 m，如图4(a)和4(b)所示;另4个点场点为高出轨面1．5 m布置，距离钢轨的距离依次为7．5，15，30和60 m，如图4(c)所示。

应用降脂汤结合针灸治疗高脂血症127例患者，其疗效为显效92例，有效28例，无效及恶化7例。总有效率94.5%。

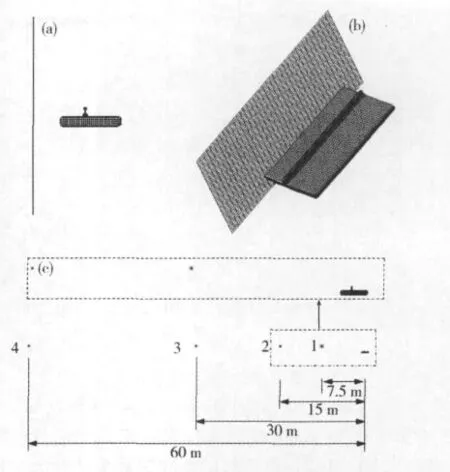
图4 场点布置图Fig．4 Layout drawings of field point

3 计算结果与讨论

将文章［12］中计算得到的振动响应结果作为位移边界条件，利用直接边界元计算轨道系统的辐射噪声，通过声辐射效率、辐射声功率及辐射声场云图对此进行综合分析。计算中取空气密度ρ=1．21 kg/m3，空气中声速 c=340 m/s。

经过计算，分别得到了钢轨与轨道板的声辐射效率，如图5和图6所示。

由图5可知:随着频率的增大，钢轨的声辐射效率也越来越大，这是因为声波的频率越高，波长也越来越小，辐射的能量相对越大。在800－3000 Hz内声辐射效率有震荡趋势，在2 000 Hz时出现1个明显的峰值，说明此时钢轨振动引起的声辐射效率较高，高频时，声辐射效率近似为1。由图6可知:当低于500 Hz时，轨道板的声辐射效率几乎成线性增长，在500 Hz时，轨道板的声辐射效率已经达到1，说明在这个频率轨道板的声辐射效率很高。

图5 钢轨声辐射效率Fig．5 Radiation efficiency of rail

图6 轨道板声辐射效率Fig．6 Radiation efficiency of track slab

计算整个时间内轨道系统的辐射声功率平均值，如图7所示。并提取4个点场点整个时间内的最大声压，如图8所示。

图7 轨道系统辐射声功率Fig．7 Acoustic radiation power of rail system

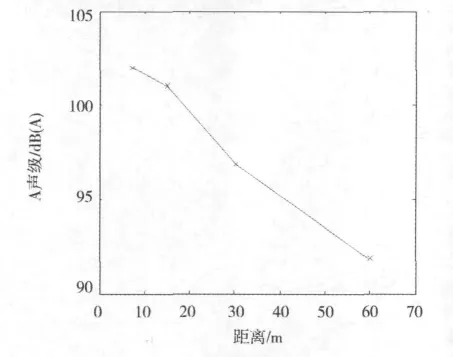
图8 点场点声压值Fig．8 The point field point sound pressure value

由图7可知:分析钢轨和轨道板对噪声的贡献量，发现轨道板的贡献主要在500 Hz以下，钢轨主要贡献是在800 Hz以上，这与上面得到的结论是一样的，即在800～3 000 Hz时主要是以钢轨的声辐射为主，在0～500 Hz时主要以轨道板的声辐射为主。

由图8可知，该图反映了轨道系统声辐射随距离变化的情况，随着距离的增长，轨道系统的声辐射呈线性递减趋势，其中最大声压为102 dB。

图9 研究线路图Fig．9 Acoustic pressure nephogram at the start time

图10 结束时刻处声压云图Fig．10 Acoustic pressure nephogram at the end time

从图9和10可知:轨道系统的声辐射随着时间的变化，有明显的传递规律。当力刚开始作用于轨道系统时，即钢轨刚接受随机力作用时，如图9所示，声辐射主要贡献区就是轨道系统接受随机力作用的区域;当力作用于轨道系统的最后时刻，如图10所示，情况与开始时刻的一样。

另外，从轨道系统表面声压云图来看，所计算轨道系统，其钢轨部位声辐射要比轨道板部位的显著，平均大15 dB左右。并且观察钢轨的表面声压云图，发现轨腰的声辐射量要比其他地方的显著。所以，若能有效降低钢轨轨腰部位的声辐射，即可有效降低钢轨的声辐射，同时也能降低轨道系统的总噪声量［18］。这也是现有许多低噪声钢轨设计从控制钢轨轨腰振动、声辐射着手的理论依据。

4 结论

(1)运用直接边界元法计算轨道系统的声辐射特性，得到了钢轨与轨道板的声辐射效率、辐射声功率和轨道系统的声场辐射云图。分析钢轨和轨道板对噪声的贡献量，发现轨道板的贡献主要在500 Hz以下，钢轨主要贡献是在800 Hz以上，即在800～3 000 Hz时主要是以钢轨的声辐射为主，在0～500 Hz时主要以轨道板的声辐射为主;随着距离的增长，轨道系统的声辐射呈线性递减趋势;钢轨部位声辐射要比轨道板部位的显著，平均大15 dB左右，轨腰的声辐射量要比钢轨其他部位的显著;

(2)首先采用有限元法求解非线性的多刚体耦合动力学，接着运用直接边界元理论计算轮轨的声辐射情况，这样计算出的轮轨滚动噪声更加接近现实情况;

(3)计算出轨道系统辐射噪声，不管与既有的且己被专家公认比较合理的模型计算结果相比，还是与实测的结果相比，本文轨道系统噪声预测的结果与这些结果都有很好的一致性，说明了本文模型与做法是合理可行的。

［1］雷晓燕，圣小珍．铁路交通噪声与振动［M］．北京:科学出版社，2004．LEI Xiao－yan，SHENG Xiao－zhen．Rail noise and vibration［M］．Beijing:Science Press，2004．

［2］Kitagawa T．The influence of wheel and track parameters on rolling noise［J］．QR of RTRI，2009，50:32 －38．

［3］Thompson D J，Jones C J C．A review of the modelling of wheel/rail noise generation ［J］．Journal of Sound and Vibration，2000，231(3):519 －536．

［4］Remington P J．Wheel/rail noise，Partl:ehara eterization of the wheel/rail dynamie system［J］．Journal of Sound and Vibration，1976(46):359 －379．

［5］Thompson D J，Jones C JC，Turner N．Investigation into the validity of two－ dimensional models for sound radiation from waves in rails［J］．Acoustical Society of America，2003，113(41):1965 －1974．

［6］Thompson D J，Jones C J C．Sound radiation from avibrating railway wheel［J］．Journal of Sound and Vibration，2002，253(2):401 －419．

［7］Nielsen J C O．Acoustic optimization of railway sleepers［J］．Journal of Sound and Vibration，2000，231(3):753－764．

［8］徐志胜，翟婉明．轨道交通轮轨噪声预测模型［J］．交通运输工程学报，2005，5(3):14 －19．XU Zhi－sheng，ZHAI Wan－ming．Prediction model of wheel－ rail noise for rail transit［J］．Journal of Traffic and Transportation Engineering，2005，5(3):14 －19．

［9］万淑敏，吴天行．铁路钢轨垂向振动的声辐射分析［J］．噪声与振动控制，2009(3):86 －89．WAN Shu－min，WU Tian－xing．Analysis of rail acoustic radiation due to vertical vibration［J］．Noise and Vibration Control，2009(3):86 －89．

［10］方 锐，肖新标．轨道结构参数对钢轨和轨枕振动特性的影响［J］．铁道学报，2011，33(3):71 －76．FANG Rui，XIAO Xin－biao．Effect of structure parameters of railway track on dynamic behavior of rail and sleeper［J］．Journal of the China Railway Society，2011，33(3):71－76．

［11］魏 伟，翟婉明．轮轨系统高频振动响应［J］．铁道学报，1999，20(2):33 －36．WEIWei，ZHAIWan－ming． Dynamicresponseof wheel/rail system to high frequency excitation［J］．Journal of the China Railway Society，1999，20(2):33 －36．

［12］刘林芽，吕 锐，刘海龙．无砟轨道垂向高频振动响应分析［J］．铁道科学与工程学报，2011，8(6):1 －6．LIU Lin－ya，LV Rui，LIU Hai－long．Vertical high frequency vibration response analysis of ballastless track［J］．Journal of Railway Science and Engineering，2011，8(6):1－6．

［13］刘林芽，刘海龙，雷晓燕．轮轨系统车轮的高频振动特性［J］．交通运输工程学报，2011，11(6):44 －49．LIU Lin－ya，LIU Hai－long，LEI Xiao－yan．High － frequency vibration analysis of wheels with wheel/rail system［J］．Journal of Traffic and Transportation Engineering，2011，11(6):44 －49．

［14］杨德庆，王德禹，刘洪林．舰艇振动声学特性数值分析［J］．上海交通大学学报，2002，36(11):87 －93．YANG De－qing，WANG De－Yu，LIU Hong－lin．Numerical analysis of vibro － acoustic characters of ship［J］．Journal of Shanghai Jiaotong University，2002，36(11):87－93．

［15］黎 胜，赵德有．半空间内结构声辐射研究［J］．船舶力学，2004，8(2):45 －51．LI Sheng，ZHAO De－you．Research on acoustic radiation in a three － dimensional half space［J］．Journal of Ship Mechanics，2004，8(2):45 －51．

［16］Moyne S L，Tebec J L．Ribs effects in acoustic radiation of a gear box－their modelling in a boundary element method［J］．Applied Acoustics，2002，63(5):223 －233．

［17］房建英，肖新标，金学松．行车速度对高速列车车轮振动声辐射特性的影响［J］．机械工程学报，2010，46(22):97－104．FANG Jian－ying，XIAO Xin－biao，JIN Xue－song．Effect of train speed on acoustic radiation characteristics of high－ speed train wheel vibration［J］．Journal of Mechanical Engineering，2010，46(22):97 －104．

［18］李再帏，雷晓燕，张鹏飞．减振型阻尼钢轨有限元分析［J］．噪声与振动控制，2009，29(4):64 －66．LI Zai－wei，LEI Xiao－yan，ZHANG Peng－fei．FEM analysis of damped rails for vibration reduction［J］．Noise and Vibration Control，2009，29(4):64 －66．