武器装备系统可靠性增长模型现状研究

2012-12-31樊胜利柏彦奇

装备学院学报 2012年5期

樊胜利，魏超，柏彦奇

（1.军械工程学院基础部，河北石家庄050003； 2.军械工程学院装备指挥与管理系，河北石家庄050003）

武器装备系统可靠性增长过程分析，是在武器装备系统的可靠性增长评定过程中，利用已知可靠性增长模型，如理想增长曲线、Duane模型、AMSAA模型和Compertz模型等，依据前期及当前试验数据，在运用最小二乘法和最大似然估计等方法确定模型参数的基础上，对下一阶段武器装备系统可靠性增长进行定量分析的研究方法。其中，可靠性增长模型是武器装备系统可靠性增长分析过程的重要组成部分。

当前，武器装备系统可靠性增长过程分析的研究重点在于：如何根据试验条件、试验环境和试验方法选择可靠性增长模型，并根据试验数据，运用参数估计法确定各参数的点估计或区间估计，从而对武器装备系统的可靠性增长趋势进行科学判定。为此，笔者对各类主要可靠性增长模型的研究现状进行了深入分析与阐述，进而为该领域的研究工作提供理论参考与借鉴。

1 方法分析与比较

1.1 方法分析

武器装备系统可靠性增长过程分析的核心内容之一是根据试验数据，利用可靠性增长模型，如Duane模型、AMSAA模型、Compertz模型、指数模型、Lloyd－Lipow模型和Dirichelt模型，分析武器装备系统可靠性增长趋势，为预测MTBF（mean time between failure）或可靠性R，估计达到可靠性指标所需试验时间提供一种科学、有效的研究方法。目前，此类可靠性增长模型较多，但主要集中在Duane模型、AMSAA模型、Compertz模型和Dirichelt模型4类。为此，文中主要对它们的研究方法进行分析与比较。

1.1.1 Duane模型

Duane模型［1－3］是一类确定性模型。它假设武器装备系统的可靠性增长是一个逐步提高，从门限值逐步增加到目标值的过程，不存在多个故障同时改进而使可靠性发生突变的可能。基于上述假设条件，Duane模型中的累积故障率和累积试验时间在双对数坐标系上趋向于一条直线，且平均故障间隔时间和瞬时平均故障间隔时间都是关于时间与增长率的线性函数。

模型参数的求解方法主要分为2类：

1）基于最小二乘拟合的参数确定法。最小二乘拟合，是以Duane模型的函数值与试验数据为基础，以二者偏差平方和最小为条件，利用极值点的偏导数为零构造方程组，通过计算增长率b和斜率a的值，对武器装备系统的可靠性增长过程进行分析与预测的研究方法。

2）基于导数最小二乘估计的参数确定法。它是针对传统最小二乘法在确定模型参数时，仅利用了曲线的静态试验数据信息，而对于曲线的动态变化规律未加以明确与说明，易导致武器装备系统在试验阶段外的适用性不高，误差较大的问题，运用各阶导数信息，以随机样本与各阶导数在概率意义下的距离之和最小为准则，以一般最小二乘法得到的模型参数为迭代初始值，对Duane模型的参数进行确定的研究方法。该方法不仅综合利用了模型导数试验信息，对曲线动态变化规律进行了分析与描述，而且通过控制模型曲线与导数变化规律实现了导数意义下的统计推断结论，提高了模型的分析与预测精度。

1.1.2 AMSAA模型

AMSAA模型［4－6］是以Duane模型为基础，利用非齐次泊松过程建立的可靠性增长模型。目前，AMSAA模型的参数求解方法很多，如作图法、回归分析法、矩估计法、最小二乘法和最大似然法等。然而，应用较多的主要为最大似然参数估计法和牛顿迭代参数估计法。

1）最大似然参数估计法。它是以武器装备系统的强度函数服从幂律过程和故障时间服从指数分布为假设条件，以n阶段武器装备系统的可靠性测试数据为基础，通过构造似然函数，利用尺度参数和增长参数的偏导数求极值的方法，得出上述参数的最大似然估计值。然而，利用最大似然估计求解参数估计值时，一般要计算联立的超越方程组，过程较为复杂，常规的迭代算法求解困难，收敛性较差。因此，在实际求解过程中：一方面利用概率权重矩阵法、双线性回归法、相关系数优化法、广义回归分析法和灰色估计等方法简化计算过程；另一方面应用模拟退火算法、蚁群算法和遗传算法等，通过加快参数求解的收敛速度，进一步提高参数的计算精度。

2）牛顿迭代参数估计法。针对AMSAA模型参数把时间t作为常量时易导致可靠性下降的问题，在AMSAA模型的基础上采用牛顿迭代法来预测某特定平均故障时间间隔下的试验时间。主要思路是：通过试验结束时的累积故障数、各故障点对应的故障时间和各个试验截止时的累积试验时间构造迭代函数，给出初始近似根及允许误差，在故障数大于或等于20的2种情况下分别预测达到预计平均寿命时的试验时间，进一步加快算法的收敛速度，提高模型的计算精度。

1.1.3 Compertz模型

Compertz模型［7－9］是由时间序列分析引申而来的，比较适用于离散型随机变量的数字特征分析。一般情况下，它假设武器装备系统寿命服从指数分布或Weibull分布。在描述武器装备系统可靠性增长速度时，认为在开始阶段的增长速度较慢，然后逐渐加快，到某点后增长速度逐渐减慢。因此，它既适用于成败型武器装备系统的试验信息，也适用于寿命型武器装备系统的试验信息。然而，它对于S型增长趋势可靠性数据的描述精度较差。

Compertz模型参数的确定方法主要分为以下3种情况：

1）Virene算法。它是把武器装备系统的可靠性增长过程分为N个阶段，每个阶段的试验组数为m，尔后把参数a，b，c的点估计转换为d的函数，并根据初值N＝0或t＝0求出X轴的截距。参数d的精度通过d的增量加以控制，最后再求出参数a，b，c的点估计。

2）非线性回归最小二乘法。它是以Virene方法确定的各类参数的点估计为基础，根据拟合曲线与数据点之间的水平距离与垂直距离的平方和最小为收敛准则，利用高斯－牛顿法将可靠性函数按泰勒级数展开，以线性项近似非线性项，用最小二乘法估计参数标正量，得到参数首次估计值。当邻近2项残差平方和迭代结果在允许误差范围内时，即得出Compertz模型各类参数的点估计值。

3）基于增长因子的线性回归法。它是通过运用增长因子表示相邻阶段武器装备系统可靠性比值，借助线性回归方法，引入随机变量（随机变量要满足Markov－Gauss假设条件），由前m阶段的可靠性评估结果预报出第m＋1阶段的系统增长因子，然后把增长因子转化为随机变量，通过第m阶段可靠性的点估计值和增长因子的分布函数，确定第m＋1阶段武器装备系统可靠性的分布函数。在试验过程中，它假设各次试验环境一致，武器装备系统的改进是逐步进行的，失效机理变化较小，Weibull分布中的形状参数变化不大，可用第m批武器装备系统形状参数的后验分布作为第m＋1批武器装备系统形状参数的后验分布（即服从Bayes相继率）。

1.1.4 Dirichlet分布模型

Dirichlet分布模型是由Mazzuchi提出的。它假设武器装备系统在m个试验阶段中，各阶段试验结果相互独立。每一阶段进行武器装备系统的修复，清除故障模式。随着“试验—改进—再试验”过程的重复进行，故障不断得到排除，武器装备系统的可靠性不断提高。

目前，Dirichlet分布模型分为2类：一是顺序Dirichlet分布模型［10－13］；二是新Dirichlet分布模型［14－15］。顺序Dirichlet分布模型的概率分布是利用Beta分布和m个阶段的可靠性或失效概率定义的1个多元Beta分布函数，参数包括α＝（α1，α2，…，αm＋1）和β。αi（i＝1，2，…，m＋1）表示第i阶段相比第i－1阶段的可靠性增量，是位置参数，可由先验信息确定；β为尺度参数，表示技术人员对α的确信程度，相对于α，β较难于确定。一般情况下，对于固定的α，β的值越大，得到的先验标准差越小，说明武器装备系统的可靠性的估计值越高。新Dirichlet分布模型则是针对只用1个形状参数β描述各个检验区间内武器装备系统可靠性的方差，不能很好符合工程需要的问题，构造了（Rk－1，1）上的Beta分布（Rk－1表示第k－1阶段武器装备系统的可靠性）。在每个检测区间内它都设有2个参数ak，bk（k表示第k个检测区间），能更准确的描述各阶段可靠性估计值以及估计值的可信度，与顺序Dirichlet分布模型相比，更具优越性。

1.2 方法比较

由上述分析可知：可靠性增长过程研究方法主要分为可靠性增长模型的选择与模型参数确定2部分。因此，研究方法的比较也主要围绕这二者展开。

1.2.1 可靠性增长模型比较

1）Duane模型和AMSAA模型的比较。Duane模型和AMSAA模型的共同之处在于二者的原理较为简单，使用方便，可操作性及适用性较强。而不同之处则主要体现在以下3个方面：①武器装备系统故障数或失效率的区分不同。在Duane模型中，它假设武器装备系统故障时间服从指数分布，故障率是常数，即固定时间间隔内的故障数是确定的，这与实际武器装备系统试验过程的吻合程度不高有关；而在AMSAA模型中，它认为故障数（失效数）和故障率均是随机变量，并认为故障数（失效数）服从非齐次泊松分布，而累积故障率则是一个以时间为自变量的分段线性函数。因此，它与Duane模型相比，其数学分析更为严密，适用面更宽，适应性更强。②模型参数的估计方法不同。Duane模型中对MTBF及参数a，b，c的估计都是较为粗糙的点估计，可靠性不高。而在AMSAA模型中，它不仅给出了各参数的点估计值，也给出了上述点估计值的置信区间，结果的可信性更高。③模型参数的物理意义不同。在Duane模型中，参数b表示增长率，而参数a的物理意义不明显；而在AMSAA模型中，参数a为尺度参数，且当b＝1时，Weibull故障率函数λ（T）＝a，MTBF服从均值为1／a的指数分布。与Duane模型相比，它的物理意义更容易理解，表示形式更为简洁，便于制定可靠性增长计划，且有利于可靠性增长过程的跟踪与评估。表1为Duane模型和AMSAA模型比较表。

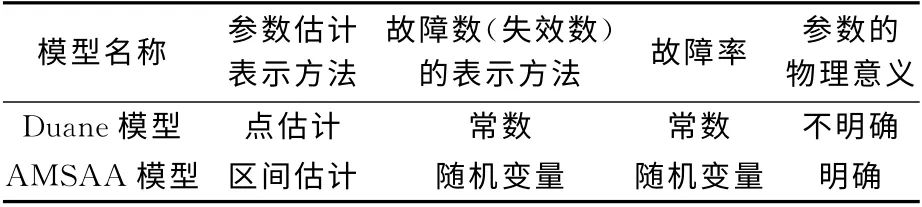
表1 Duane模型和AMSAA模型比较

2）Compertz模型与AMSAA模型和Duane模型的比较。Compertz模型与上述2种模型相比较，主要区别有以下3方面：一是由于Compertz模型是来源于时间序列分析的一种可靠性增长模型，因此它更适用于成败型武器装备系统的可靠性增长过程分析；二是它不涉及累积故障时间、故障率和失效率等参数，而主要由a，b，c，d等4个参数决定；三是对于具有S型增长趋势的可靠性数据，它的描述精度较差。

3）次序Dirichlet模型和新Dirichlet模型的比较。次序Dirichlet模型和新Dirichlet模型都是Bayesian可靠性评定模型的一部分。它是针对采用无信息先验试验或试验信息折合方法易导致评估结果可信性不高的问题提出的。二者的共同之处在于：一是它们都是Bayesian可靠性评定模型中各阶段武器装备系统可靠性向量的先验分布函数；二是它们都能够把边缘分布和联合分布特性与专家意见、经验和同类武器装备系统的试验信息相结合，进行准确的可靠性增长过程分析与管理。其不同之处则主要包括以下3个方面：①工程的适用背景不同。次序Dirichlet模型只用1个参数β描述检测区间武器装备系统的可靠性方差，其工程适用性不强；而新Dirichlet模型则可用2个参数ak，bk来描述各阶段武器装备系统可靠性估计值及估计值的可信度，其工程适用性较好。② 先验密度函数有差异。次序Dirichlet模型的先验密度函数是单峰值函数，当参数β取值较大时，各阶段的先验方差较小，易导致先验分布的主导性过强，试验结果对后验推断的影响较小；而新Dirichlet模型则利用各检测区间参数ak，bk解决了此问题。③参数的物理意义不同。次序Dirichlet模型参数的物理意义明显，ai（i＝1，2，…，m）表示第i阶段可靠性增量，β为尺度参数，表示技术人员对上述参数的确信程度；而在新Dirichlet模型中参数的物理意义不明显，难以用先验信息直接确定，易导致可操作性不强的问题。

1.2.2 可靠性增长模型参数求解方法比较

可靠性增长模型的参数求解方法较多，文中主要列举了导数最小二乘估计、最小二乘拟合、非线性回归最小二乘拟合、Virene算法和最大似然估计等方法。因此，笔者主要对上述方法的异同点进行详细的比较与分析。

1）参数估计的评价标准。从参数估计结果看，参数估计方法不同，估计量会有差别。因此，在评价参数估计量时，一般都会以无偏性、有效性和相合性等3方面进行比较。而以最小二乘法为基础的各类参数估计方法同最大似然估计相比，其有效性和无偏性较差。

2）参数应用的简易程度。以最小二乘法为基础的各类参数估计方法是通过图形观察，得出数据分布具有简单的线性或非线性特征后，以误差平方和最小为判定准则求解参数的计算过程。在应用过程中简便、易行，可操作性较强；而最大似然估计则必须知道各样本的概率密度函数，相比较前者而言，它的可操作性的难度更高。

3）模型参数的求解速度与精度。最大似然参数估计法与最小二乘法在求解模型参数时，对于较为复杂的问题，都需要建立超越方程组，求解速度较慢，而且参数的求解精度与收敛性不易控制；Virene算法、非线性回归最小二乘法和基于增长因子的线性回归法，是通过简化计算步骤，以线性项近似非线性项等方法，达到加快求解速度的目的。然而，精度较差；基于遗传算法和模拟退火算法等智能算法的模型参数求解法，是通过设置退火温度、遗传代数等方法，依据全局收敛的思想，实现参数求解从局部最优向全局最优的转化，提高参数的求解速度。然而，计算时间较长。

2 存在问题及改进方向

通过对可靠性增长模型的分析与比较可以看出，目前仍存在以下3方面问题：

1）在AMSAA模型中，当t→＋∞时，强度函数ρ（t）不收敛。

2）在武器装备系统可靠性增长过程分析中，样本异总体的问题将会对可靠性分析产生较大影响，特别是现场试验为小样本时更加明显。因此，如何体现不同试验阶段武器装备系统可靠性的差异性与相似程度，也是可靠性增长模型存在的问题之一。

3）可靠性增长模型的尺度参数β是技术人员对估计值的确信程度，也是对先验信息不确定的一种弥补措施。然而，它也不可避免的引入了主观因素，易影响结果的可信度。

针对上述存在问题，笔者认为应从以下3方面进行改进：

1）在AMSAA模型的强度函数中引入随机变量，完成其收敛过程的分析与判断；

2）在使用Bayes方法确定先验分布时，应在共轭先验分布中引入继承因子与更新因子，减少历史样本与样本异总体对武器装备系统可靠性的影响；

3）对于Dirichlet模型的尺度参数β，在量化过程中引入语言值与隶属度函数，使数值的量化结果更为准确、客观，减少人为因素的影响。

3 结论

系统性与复杂性是武器装备的重要特征。在武器装备系统的研制与发展过程中，它必须经过“试验—分析—改进—再试验”的过程，才能不断提高武器装备系统的可靠性。因此，进行武器装备系统可靠性增长分析，是减少序贯试验次数，节约研制经费，缩短研制周期，不断改进与完善武器装备系统可靠性的重要手段与方法。基于此，文中对可靠性增长模型，如Duane模型、AMSAA模型和Compertz模型等，进行了详细的分析与比较，并指出了存在问题与改进方向，希望能为武器装备系统可靠性增长研究提供理论参考与借鉴。然而，文中对其他诸如指数模型、Lloyd模型和Lipow模型等，并没有展开集中论述，而且可靠性评估和故障分析作为可靠性增长过程的重要内容，也有待于下一步继续深入研究与探讨。

（

）

［1］姜健，马振龙，姜悦岭.Duane模型的推广［J］.哈尔滨师范大学学报：自然科学版，1997，13（5）：83－86.

［2］王桂华，张连祥.采用Duane模型评估航空发动机平均故障间隔时间［J］.航空发动机，2006，32（1）：29－30.

［3］任建军，杨云，常文兵，等.Duane模型在确定装备可靠性门限值中的应用［J］.系统工程与电子技术，2004，26（8）：1148－1154.

［4］吕海峰，戴新生，王鹏，等.离散AMSAA模型在火箭发动机可靠性增长分析与评定中的应用［J］.弹箭与制导学报，2008，28（1）：171－176.

［5］代进进，李相民，刘振.基于AMSAA模型的装备可靠性增长评估方法［J］.舰船电子工程，2007，27（3）：213－215.

［6］张立民，孙永威，周帆.基于AMSAA模型的弹上电子设备可靠性增长试验研究［J］.计算机与数字工程，2010，38（2）：18－21.

［7］尹瑛，徐吉辉，端木京顺.基于非线性回归最小二乘法的改进Compertz模型参数估计［J］.空军工程大学学报：自然科学版，2005，6（6）：77－79.

［8］刘琦，冯静，周经伦.基于Compertz模型的液体火箭发动机可靠性增长分析［J］.航空动力学报，2004，19（3）：419－423.

［9］王玮，周海云，尹国举.使用混合Beta分布的Bayes方法［J］.系统工程理论与实践，2005（9）：142－144.

［10］姚宗静，佘强，邱荣.基于一般Dirichlet过程的非参数贝叶斯分析［J］.河南师范大学学报：自然科学版，2010，38（3）：8－10.