基于(T,s,S)策略的维修器材联合订购模型与算法
2012-12-31张建荣邢联大苏振华罗广珂
张建荣, 邢联大, 苏振华, 罗广珂
(1.军械工程学院 装备指挥与管理系,河北 石家庄050003; 2.空军驻山西地区军事代表室,山西 太原030006; 3.94754部队)
维修器材库存管理是装备保障管理工作中的一项重要内容。为应对作战和训练需求,维修器材仓库往往储备大量的维修器材。由于现有装备的可靠性和维修性还不够高,仍然需要把维修器材作为保持战备完好性的手段,但这种方法也导致了费用提高和其他一些问题。尽管如此,提高装备战备完好性的途径非常有限,维修器材在相当长一段时间内仍是维持战备完好性的最有效手段[1]。
由于维修器材需求的不确定性,使得进行战时维修器材供应保障决策时难以定夺,依靠传统大量预置储备的理念,虽然保障了战斗力,但会因增加成本造成浪费;而供应不足又将影响作战效能[2]。因此如何尽可能地满足不确定需求以获得最佳军事经济效益是战时维修器材供应保障工作的关键,采取联合订购是一种可行的办法。
多品种维修器材联合订购问题属于联合补充问题(joint replenishment problem,JRP)。针 对随机性JRP问题,国内外很多学者也进行了广泛研究,并提出了很多有实际意义的策略[3-4]。根据库存检查方式不同,联合补充策略可以分为定周期补充策略(periodic replenishment policy)和连续补充策略(continuous replenishment policy)。最典型的联合补充策略有3种:文献[5]提出的可订购点(s,c,S)策略;文献[6]和文献[7]提出了组订购点(Q,S)策略,后来文献[8]对需求服从泊松分布的该策略进行了研究;文献[9]提出了周期性补充策略(T,S)策略,每个订购间隔周期将所有品种的物资订购至最大库存。前2种策略都属于连续补充策略。在(T,S)策略中,各种物资定期补充而不考虑其每个周期的库存水平。这样做可以更具有柔性,更大程度上体现聚集效应,降低固定订购成本,但是订购任何一种物资都应该考虑其库存位置。
本文提出了(T,s,S)策略,该策略可以比定周期统一订购策略提供更大的柔性。其中,T表示库存检查间隔时间;s和S分别表示库存器材的订货点和最大库存量。按照该策略,库存的每种器材采用定周期检查库存的方式。每种物资采用一种独立的,定周期的(s,S)策略。每隔T时间检查一次库存,如果器材i的库存水平低于或等于其订购点,则补充至最大库存Si。每个周期发出订购申请,并支付一次运输启动成本。
1 模型设计
定周期检查库存的联合补充策略适用于需求波动比较平稳,上级供应及时,运输条件有利的情况。从器材种类上来说,该策略适用于重要度和缺货风险都不是很大的种类,但这些器材在库存数量中往往占据较大份额。定周期检查库存方式下,不需要持续监视库存水平变化。因此采用定期检查库存的策略可以节省更多时间和精力来管理其他重要的维修器材。本文不考虑维修器材的修复,并假定其需求服从正态分布。
1.1 符号约定
模型中用到的符号约定如下。
i为第i种维修器材;n为参与联合订购的器材数;K为运输启动成本;ki为器材i的可变运输成本;T为订货间隔周期;Ci(T)为第i种器材的单位时间可变运输成本和库存保管费用和;C(T)为单位时间库存费用的总期望值;λi为器材i的需求率服从已知的分布;hi为单位库存单位时间的保管费用;L为订购提前期,为常数,为简化计算,规定L<T/2,即不会出现交叉订购,每个时间段都只有一个在途订单;Di为随机变量,表示第i种器材单位时间的需求量;Si为器材i的最大库存量;si为器材i的订购点;α为服务水平,订购周期内维修器材需求被满足的概率。
1.2 策略流程
(T,s,S)策略运作流程如图1所示。可能发生缺货的时间有2个阶段:上次器材供应到货到下一次订购时这段时间内;补货提前期内,缺货采用补足处理。
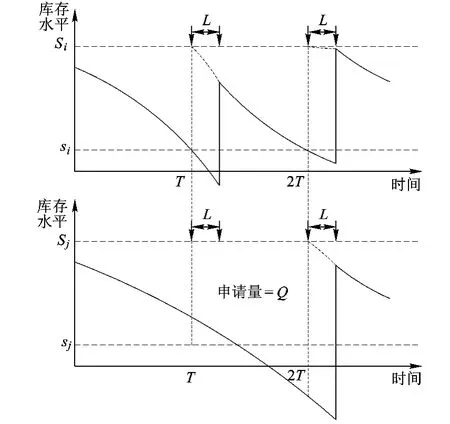
图1 (T,s,S)策略运作流程
某个库存盘点时刻,可能所有器材的库存都大于订货点,那么这个周期就不需要订货,可以节约运输启动成本。但只要订货点的设计合理的话,这种概率是很小的,所以可以忽略。假定每个盘点时刻至少有一种器材的库存水平低于订货点。这种策略是对现行单品种(s,S)策略的改进,是最容易改造后在实际工作中实施的一种策略,研究它的意义也正在于此。
1.3 建立模型
订货间隔周期T的长度,可根据最小费用来确定,也可根据维修器材供应实际需要事先确定。本文搜索最佳T的方法是根据费用最小确定的。如果T已知,设T等于确定型模型的基本订购间隔时间。间隔时间为T的周期性订购(s,S)策略下,总费用为
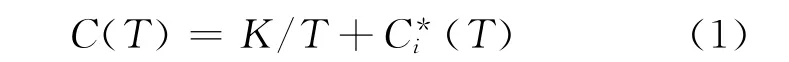
C*i(T)是物资i的单位时间(s,S)策略的费用,其中订购间隔时间为T。假定(s,S)策略的成本计算只与可变运输成本ki相关,故可采取求解单品种策略的方法求解这2个参数。实际上,(T,s,S)策略的费用要比式(1)的低。因为如果在1个周期内1个维修器材都没有订购的话,固定订购费用K是不会产生的。经分析认为可忽略这一差异,即每次至少有一种物品会低于订货点。
2 算法设计
T与(s,S)参数分别确定,故可分开设计算法,采用RAND算法求解T,(s,S)参数则采用一种近似求解方法,这样可以降低算法的难度,减小计算的工作量。
2.1 T参数的求解算法
文献[10]结合Goyal和Silver算法的优点,提出了具有重要影响的RAND算法。该算法将T的有效区间分为均等的m段,形成m个T的初始值,应用Silver的改进算法来求解T的初始值。RAND算法的步骤如下。
Step1 由式(2)计算系统的基本订购周期的最大值和最小值
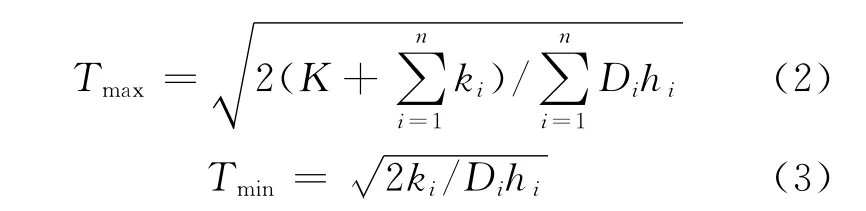
Step2 把[Tmax,Tmin]分为m等分,得到初始值(T1,…,Tj,…,Tm),m由决策者决定;设j=0。
Step3 设j=j+1,r=0。
Step4 设r=r+1,对每个Tj计算每种维修器材的周期乘子bjr,即
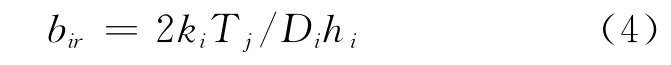
Step5 寻找Tj下的最优周期乘子b*ir=L,如L(L-1)<b2ir≤L(L+1)。
Step6 计算新的基本订购周期时间,即
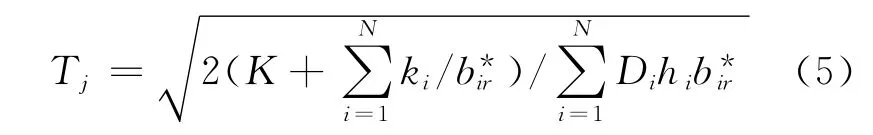
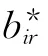
2.2 (s,S)参数的求解算法
2.2.1 最大库存量S的确定
确定最大库存量最简单的方法就是参照基本经 济 订 货 批 量(economic odering quantity,EOQ)来确定,采用期望值将随机需求处理为确定性的恒定需求,这在工程实现上是可以接受的。不过,由于S是订单发出后库存水平达到的目标,在决策时刻如果发出订单,则订购至最大库存量S。也就是说,如果需求是批量出现的,则每次补货批量不是固定不变的,Qi=Si-si。如果需求是逐个出现的,则等同于固定订购量模型。s是正常订购的参照点,这样利用EOQ计算出来的补货批量就对应于S与s的差值。需求取其均值λ,则补货目标为
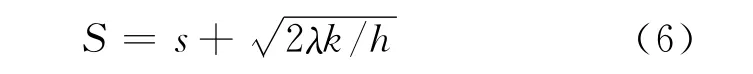
2.2.2 安全库存与订货点s的确定
单位时间的需求量D是随机变量,均值为λ,方差为σ2。订购提前期内的总需求量DL的均值为λL=λL,方差为σ2L=Lσ2,用FL(x)表示DL的概率分布函数。
盘点周期内的总需求量DT的均值为λT=λT,方差为σ2=Tσ2,用FT(x)表示DT的概率分布函数。
与连续性盘点不同,周期性判断订货点库存要满足的需求所对应的时间段不仅仅是订购提前期,还包括一个盘点周期。因为采用周期性盘点时,在盘点时间刻可能补货也可能不补货。如不补货,则补货的机会就在下一个盘点时刻。由此可知,在采用周期性盘点时,满足维修器材需求的服务水平是指(T+L)时间范围内的。安全库存及订货点s是基于(T+L)时间内总需求量来确定,其值为s=λ(T+L)+ss。其中,λ(T+L)=λT+λL,是(T+L)时间总需求量的期望值;ss为安全库存。图2表示(s,S)策略下的安全库存。
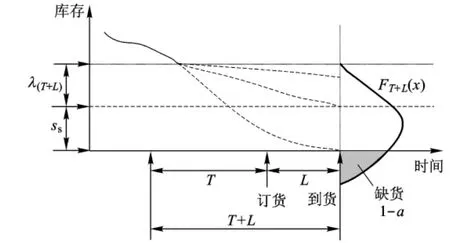
图2 (s,S)策略下的安全库存
假设要求服务水平不低于α。对于维修器材这样离散类型的货物,订货点应该是满足式(7)最小的s:
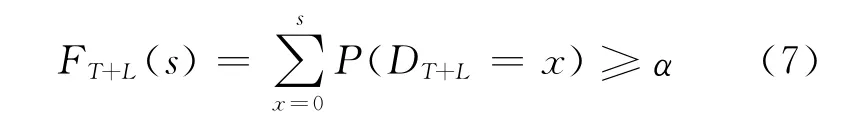
对于给定的服务水平要求α,查标准正态分布面积表可获得对应的安全系数z。每周期的订货点除满足提前期内需求量外还要满足盘点周期内的需求量,因此得到
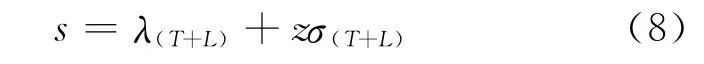
式中zσ(T+L)即 为 安 全 库 存 量,其 中σ(T+L)为 标准差。
根据维修器材的使用数据,按预测周期R,选择合适的预测方法对维修器材的需求量进行预测,得到λR和σR。假设各品种维修器材的需求量独立同分布,可得:
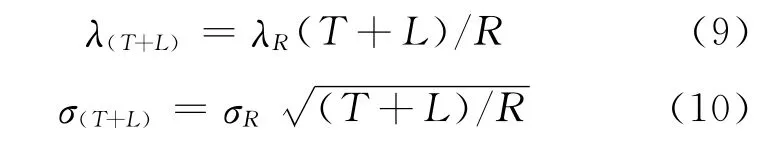
3 算 例
某军区器材仓库,选择10种器材作为研究对象,已知运输启动成本K=500元,订购提前期L=1/12;维修器材需求服从正态分布,其他数值如表1所示。
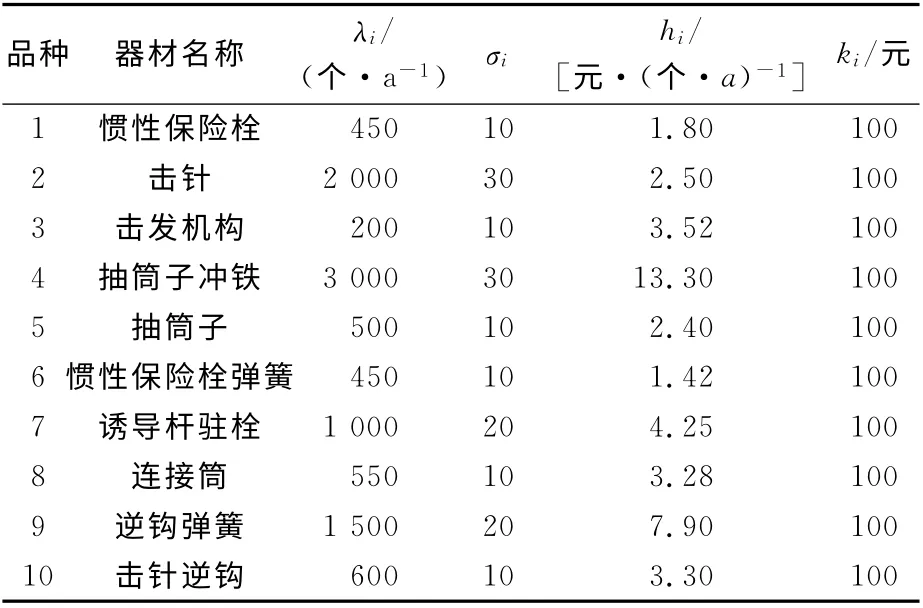
表1 算例数据
根据文献[11]得到保障度为P=0.95时(T,S)策略的解,采用本文的算法求解可以算得保障度为P=0.95时(T,s,S)策略的解,2种策略结果比较如表2所示。
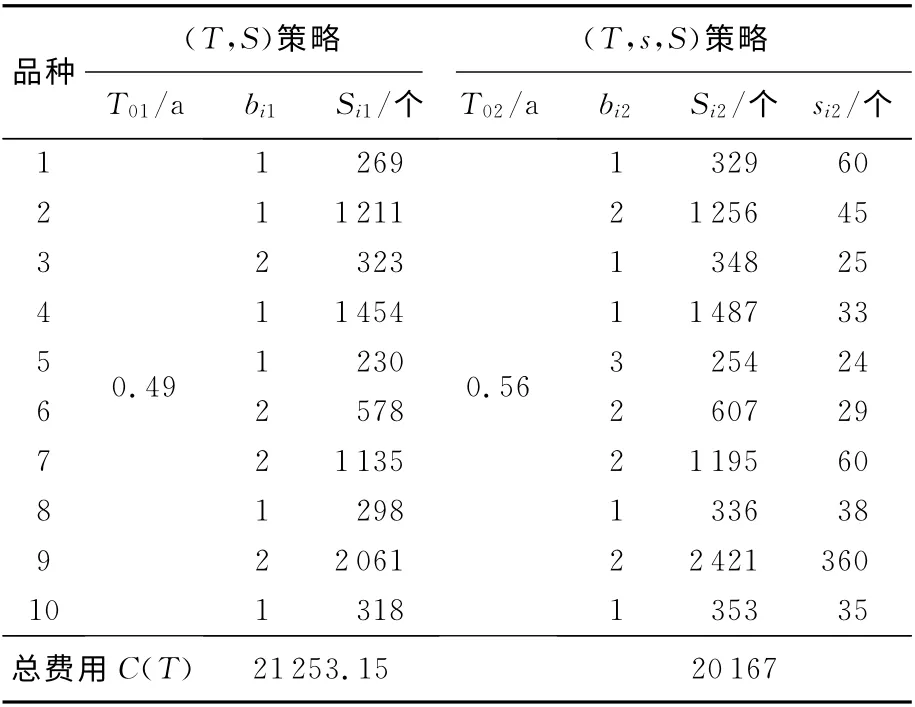
表2 (T,S)策略和(T,s,S)策略的解
从表2可看出,当保障度为P=0.95时,(T,s,S)策略比(T,S)策略的经费节省率为
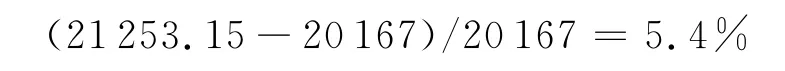
可以看出(T,s,S)策略比(T,S)策略的经费要节省。同理,在相同费用约束下,新策略的服务水平会更高。此外,(T,s,S)策略的库存检查周期更长一些,可以减少单位时间内的订购次数。
4 结 束 语
本文所提出的(T,s,S)策略只是维修器材联合订购策略中的一种,所采用的算法并非一定是最优,但它与(T,S)策略比较所产生的效果,简化了模型复杂程度,减少了算法工作量。根据要求的满足率确定订货点的方法可以确保维修器材服务水平,对维修器材库存控制不失为一种满意的方法。同时有多个在途订单的情况也是现实维修器材保障活动中常见的现象,用本文的方法无法描述这种情况,这也是下一步研究的方向。
(
)
[1]宋太亮.装备保障性工程[M].北京:国防工业出版社,2002:95-99.
[2]刘喜春.不确定需求下航空维修器材多阶段供应保障规划模型及动态协调机制研究[D].长沙:国防科技大学,2009:3-4.
[3]JOHSON E L.Optimality and computation of(q,s)policies in the multi-item inventory systems[J].Management Science,1967,13(1):475-491.
[4]NADDOR E.Optimal and heuristic decisions in single and multi-item inventory systems[J].Management Science,1975,21(11):1234-1249.
[5]BALINTFY J L.On a basic class of multi-item inventory problems[J].Management Science,1964,10(1):287-297.
[6]RENBERG B,PLANCHE R.A model of multi-item inventory replenishment policy for simulation[J].Operational Research,1967(6):47-59.
[7]PANTUMSINCHAI P.A comparison of three joint ordering inventory policies[J].Decision Sciences,1992,23(1):111.
[8]ATKINS D R,IYOGUN P O.Periodic versus can-order policies for coordinated multi-item inventory systems[J].Management Science,1988,34(6):791.
[9]HANS BLANC.Advanced inventory management:models and algorithms[M].Tilburg:Tilburg University,2011:32-34.
[10]KAPSI M,ROSENBLATT M.On the economic ordering quantity of jointly replenished items[J].International journal of Production Research,1991(29):107-114.
[11]高静,李成严.随机型联合补充问题的混合遗传算法的研究[J].哈尔滨理工大学学报,2008,13(2):11-14.
