一种空间可展开桁架结构杆件热膨胀系数的优化设计

刘振玉 冯纪生 张庆君

（北京空间飞行器总体设计部，北京 100094）

1 引言

空间可展开桁架结构尺寸较大，在空间经历恶劣的温度环境，往往受热变形的影响较大，特别是桁架结构支撑的平板阵列天线，为确保高精度、高分辨率的要求，通常对天线形面保持精度要求特别高，这就给结构设计提出了苛刻的要求［1］。

例如太阳同步轨道卫星，暴露在空间环境中的天线结构，其温度范围甚至超过（-100 ℃，100 ℃）的区间。温度的剧烈变化引起天线支撑桁架结构的变形，进而影响天线的形面精度，致使天线的电性能下降，因此必须对桁架结构进行热变形分析，对影响桁架热变形的主要因素进行参数设计［2］。

卫星设计时，往往需要根据天线精度的总体要求，通过精度分配，给出桁架结构热变形允许的最大值，并以此最大允许变形参数为前提，进行桁架结构设计，对相关因素进行参数预算，以便对桁架杆件参数提出指标要求。对于热变形来说，主要是杆件的轴向热膨胀系数（以下简称热膨胀系数）必须满足要求。传统的方法是利用经验法进行试凑，以经验热膨胀系数作为初值，计算桁架的变形大小，如果超出最大热变形的约束条件，就重新代入一组更优的值，直到满足要求为止，这样做虽然能满足工程实际的要求，但效率较低，费时费力。

本文提出了一种在给定最大热变形约束下，通过分析各杆件热膨胀系数对桁架热变形的影响，并计算了各杆件敏度，根据敏度绝对值的大小对杆件进行分组，采用工程优化的思想，计算热膨胀系数所能允许的可行范围的方法。

2 研究对象

本文以支撑某平板天线的空间可展桁架结构为研究对象，如图1所示。桁架由24根杆件和杆件之间的铰链及接头组成（为计算方便，对各杆件进行统一编号）。杆件材料为碳纤维环氧复合材料，形式为中空的管；铰链及接头主要为钛合金，形式为实心圆柱。其中，杆件1、杆件2、杆件3、杆件4和杆件12、杆件13、杆件14、杆件15组成两个平板天线的安装框架。

图1 可展开天线支撑桁架结构及杆件编号Fig．1 Truss structure of the deployable antenna and the numbers of bars

此桁架结构在空间环境下，由于温度的剧烈变化，会引起杆件的轴向伸缩，从而导致结构的变形。特别是天线安装框架的变形，会严重影响天线的电性能，必须加以控制。通过杆件热膨胀系数的设计，可以使天线安装框架的变形控制在允许的范围内，以确保天线形面的精度满足要求。

3 传统杆件热膨胀系数计算方法

在空间桁架结构杆件的热膨胀系数设计中，传统方法是利用经验值进行试凑，其设计流程如图2所示。

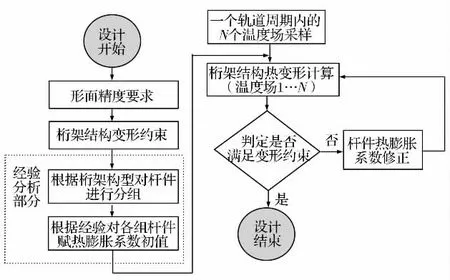
图2 传统热膨胀系数设计流程Fig．2 Flow diagram of conventional the design of the coefficient of thermal expansion

在桁架构型尺寸确定的情况下，设计师根据桁架结构构型特点对杆件进行简单分组，再根据国内外相关型号经验选定一组初值［3］，利用有限元软件进行热变形计算，通过分析一个轨道周期内不同温度场下的变形情况，找到桁架的最大变形量，如果此变形量不满足约束要求，就代入一组更优的热膨胀系数进行计算，直到找到符合热变形约束要求的值为止。需要特别强调的是受目前工艺水平的限制，不是任何热膨胀系数的杆件都能生产，部分对热膨胀系数要求较高的杆件目前还不能生产，这就要求设计人员在确定杆件参数指标时必须科学合理，既要满足热变形指标要求，又要考虑目前的工艺水平。经验试凑法只能找到一组离散的值，因此，其具有一定的局限性，显然，如果能通过计算，找到一个杆件热膨胀系数的可行范围是一件很有意义的事。

4 基于优化设计的杆件热膨胀系数计算方法

针对经验试凑法可能存在的局限性，本文采用工程优化的思想，提出了基于敏度分析对杆件进行分组、以及基于优化设计计算杆件热膨胀系数所允许范围的方法，供工程应用参考使用。本文采用西门子公司的I-DEAS软件作为热分析软件，采用MSC 公司的PATRAN／NASTRAN软件进行结构有限元分析，其设计流程如图3所示。

图3 基于优化分析的热膨胀系数设计流程Fig．3 Flow diagram of the design of the coefficient of thermal expansion based on the optimization analysis

设计流程具体实现如下：

（1）有限元建模，在I-DEAS软件中进行有限元建模，分别建立桁架结构的热分析模型和结构分析模型；

（2）温度场计算，分析卫星一个轨道周期内的温度场，根据时间对温度场进行采样，得到在同一个周期内的N个温度场采样，记作T1…TN；

（3）温度场数据映射，利用I-DEAS软件自带的Mapping命令［4］，将热分析模型的温度场数据映射到结构分析模型上，并利用软件的NASTRAN 接口，将此带有温度场数据的结构分析模型导入到PATRAN 软件中；

（4）杆件分组，选择第i个温度场Ti，计算各杆件对热变形的敏度，以杆件敏度绝对值占所有杆件敏度绝对值之和的某一比值为阈值（此阈值可以根据工程实际情况进行选取），敏度绝对值大于此阈值的杆件划分为敏感杆件，其余杆件归为不敏感杆件；重复计算N个采样温度场下的敏度情况，将各温度场下的敏感杆件取并集，归为敏感杆件组，其余杆件归为不敏感杆件组；

（5）确定热膨胀系数范围，将敏感杆件组的热膨胀系数设为设计变量，不敏感杆件组的热膨胀系数取某一工程易于达到的初值，在预定的热变形约束条件下，通过优化计算，得出敏感杆件组的热膨胀系数范围；

（6）参数设计及验证，在（5）所求得的热膨胀系数范围内，采用优化的方法进行参数设计，找到一个优值，通过计算此优值下的变形量是否小于约束条件来进行验证。

5 算例分析

基于图1所示的桁架结构，采用图3所描述的计算流程及方法进行具体算例分析。

5．1 温度场计算

在桁架结构热变形分析中，温度场数据是分析的前提条件。卫星在轨道上运行，温度场非常复杂，为确保结构设计满足热变形要求，往往需要找到最“恶劣”的温度场极端工况，即结构变形最大时的温度场。结构设计时，必须要求极端工况下结构热变形量控制在允许的范围内。卫星在轨道上要经历周期性的温度场变化，而且温度场受光照、遮挡、星体辐射等影响，往往非常复杂，因此要准确找到一个周期内的极端温度场工况非常困难，一种可行的近似措施是使用均匀采样法，在一个轨道周期内，对温度场进行采样，如每隔一个时间间隔采样一次温度场数据，通过计算每个样本温度场下的结构热变形，获得一组温度场与结构热变形的关联数据，最后通过数值拟合或简单取变形量最大值的方式，确定极端温度场工况，若要提高计算精度可以减小采样间隔。在本文中为分析的简化，不失一般性的选取两个典型工况：光照工况（卫星在光照区时的温度情况）和阴影工况（卫星在阴影区时的温度情况）进行实例分析。

利用I-DEAS 软件建立桁架结构的有限元模型：热分析模型和结构分析模型。热分析模型主要用于温度场的计算，结构分析模型用于结构热变形计算。需要说明的是，在本文中，结构分析采用NASTRAN 软件，因此在I-DEAS软件中建立的结构分析模型主要用于温度场的映射，为将温度场无缝导入NASTRAN 中做准备，以实现机-热一体化集成分析。利用所建立的热分析模型，计算桁架结构在所选定的两个典型工况下的稳态温度场，再利用I-DEAS软件中自带的Mapping 命令，将计算所得的温度载荷映射到结构分析模型上，这样就在I-DEAS软件中获得了带有温度载荷的结构分析模型，再利用I-DEAS软件的NASTRAN 接口，将此结构分析模型导入到PATRAN 中，这样就自动在PATRAN 中获得了带有准确温度场数据的结构分析模型，从而实现I-DEAS 与PATRAN／NASTRAN 之间的无缝结合。

5．2 杆件分组

利用5．1节获得的带有温度场载荷的结构分析模型，在NASTRAN 中分别计算两个典型工况下各杆件的敏度，再利用设定的阈值对所有杆件进行分组，这样就在每个温度场中将所有杆件分为两组：敏感组和不敏感组，将每个温度场下求得的敏感杆件取并集，获得所要求的敏感杆件组，其余杆件归为不敏感杆件组。

经计算，在所选定的两个典型工况下各杆件的敏度如图4所示。

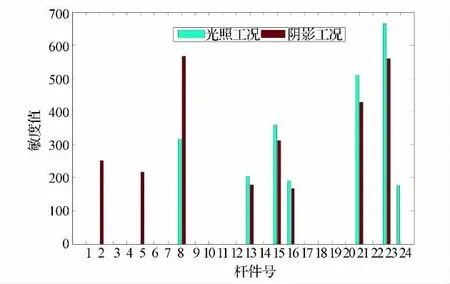
图4 各杆件的敏度Fig．4 Bars’sensitivity to the coefficient of thermal expansion

由图4可知，杆件编号为2、5、8、13、15、16、21、23、24的9根杆件为敏感杆件组，其余为不敏感杆件组。

5．3 杆件热膨胀系数范围计算

在工程中，平板天线形面精度主要受桁架底部安装框架的热变形影响。平板天线与桁架安装框架在X、Y方向上采取游离连接，隔离变形传递，因此，在计算过程中，取桁架安装框架的Z向位移变形为研究目标，在本算例中暂取0．8 mm 作为最大变形约束条件，工程实际计算可以根据需要调整。

通过对工程需求的分析，建立结构的优化数学模型如下：

1）取位移下限时（变形沿-Z方向）

2）取位移上限时（变形沿＋Z方向）

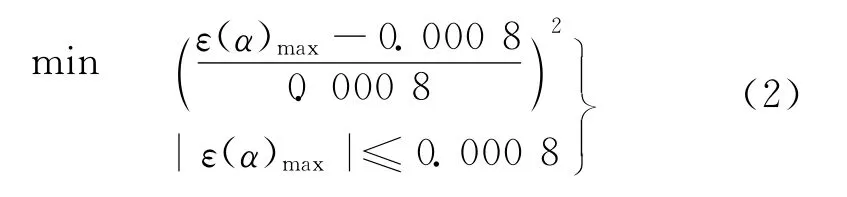
式中：α为敏感杆件组热膨胀系数，作为设计变量；为目标函数，ε（α）max表示安装框架上Z向的最大位移。

将不敏感杆件组热膨胀系数取某一工程易于达到的初值（在本算例中取3．0×10-6K-1），通过优化分析得出两种典型工况温度场下热膨胀系数范围如表1所示。

表1 两种典型温度场下热膨胀系数范围Table 1 Ranges of the coefficient of thermal expansion with two kinds of typical temperature field

取两种典型工况下热膨胀系数范围的交集，可得所要求取的敏感杆件组热膨胀系数范围为［-5．716 7×10-7K-1，2．645 2×10-6K-1］。即在所选的两个典型温度工况下，当编号为1、3、4、6、7、9、10、11、12、14、17、18、19、20、22的杆件热膨胀系数取值3．0×10-6K-1时，对于编号为2、5、8、13、15、16、21、23、24的杆件，只要其热 膨胀系数在［-5．716 7×10-7K-1，2．645 2×10-6K-1］范围内，就能满足桁架结构安装框架Z向最大变形不超过0．8mm的约束条件。

5．4 校验及参数分配

为了校验本文提出的热膨胀系数范围的优化设计方法，对5．3节所求取的范围进行验证，根据所求得的热膨 胀系数范围［-5．716 7×10-7K-1，2．645 2×10-6K-1］，从下限值到上限值，进行取整验证，分别计算当热膨胀系数取不同值时的结构最大热变形。由于本文只研究桁架结构的Z向最大位移，根据桁架结构形式，由于靠近卫星箱体一侧的边界条件约束了除绕Y轴转动外的其他五个自由度，在桁架结构安装框架平面上，结构Z向变形的最大位移必定出现在最外端前后两侧的398或者399号节点处，如图5所示。

图5 最大变形部位示意图Fig．5 Schematic diagram of maximum deformation location of the structure

因此验证桁架结构最大位移变形时，只需考虑398号节点和399号节点的位移值即可，计算结果如图6所示。

图6 热膨胀系数取值与位移关系图Fig．6 Diagram of relationship between the value of the coefficient of thermal expansion and the displacement of the structure

由图6可以看出，当敏感杆件组热膨胀系数范围取值［-5．716 7×10-7K-1，2．645 2×10-6K-1］时，结构最大变形满足0．8mm 的变形约束，特别是当敏感杆件组取两端点值时，可以计算出安装框架Z向最大变形分别为0．795 mm（取下限-5．716 7×10-7K-1时）和-0．8mm（取上限2．6452×10-6K-1时）。

利用NASTRAN 的优化功能，在所求取的杆件热膨胀系数范围内进行参数分配，计算出结构的最佳热膨胀系数为-2．579 5×10-7K-1。工程上，往往需要对此值进行取整处理，因此取优化值为-2．5×10-7K-1。经计算验证，当敏感杆件组的热膨胀系数值设定为-2．5×10-7K-1时，安装框架Z向的最大变形量为0．65mm。

需要特别说明的是，由于本算例所分析的桁架结构并不对称，且各杆件对热变形的影响各不相同，互相影响，互相制约，致使要求取一组各杆件热膨胀系数的最优范围值极其困难，利用本文所使用的方法所得的结果也只是工程可行解，并不是最优解，如果约束范围精度进一步提高，要得到比较好的解，需要调整不敏感杆件组的热膨胀系数初值。

6 结束语

本文针对桁架结构的热膨胀系数设计，提出了一种在给定最大热变形约束下，基于敏度分析对杆件进行分组、以及基于优化设计确定杆件轴向热膨胀系数极值，从而确定其所能允许的可行范围的方法，该方法相比于传统靠经验试凑法确定桁架杆件热膨胀系数的情况，提高了计算效率和计算精度。

（References）

［1］袁家军，陈烈民．卫星结构设计与分析［M］．北京：中国宇航出版社，2004

Yuan Jiajun，Chen Liemin．Satellite structure design and analysis［M］．Beijing：Astronautic Press，2004（in Chinese）

［2］闵桂荣．卫星热控制技术［M］．北京：中国宇航出版社，1991

Min Guirong．Thermal control technology of satellites［M］．Beijing：China Astronautic Press，1991（in Chinese）

［3］彭成荣．航天器总体设计［M］．北京：中国科学技术出版社，2011

Peng Chengrong．System design for spacecraft［M］．Beijing：China Science and Technology Press，2011（in Chinese）

［4］麻慧涛，李劲东．大型复杂空间结构机-热集成分析技术研究［J］．宇航学报，2008：29（2）：413-419

Ma Huitao，Li Jindong．Integrated thermal-structural analytical technology for space structure with large-scale and complicated construction［J］．Journal of Astronautics，2008：29（2）：413-419（in Chinese）

［5］张淑杰．空间可展桁架结构的设计与热分析［D］．杭州：浙江大学，2001

Zhang Shujie．Design and thermal analysis for deployable space truss structures［D］．Hangzhou：Zhejiang University，2011（in Chinese）

［6］杨玉龙．空间展开桁架结构设计理论与热控制研究［D］．杭州：浙江大学，2007

Yang Yulong．Structure design theory and thermal control study for space deployable truss structure［D］．Hangzhou：Zhejiang University，2007（in Chinese）

［7］张立华．有限元法在空间飞行器天线反射器热分析中的应用［J］．中国空间科学技术，1999，（1）：32-37

Zhang Lihua．Application of finite element method in the thermal analysis of spacecraft antenna reflector［J］．Chinese Space Science and Technology，1999，（1）：32-37（in Chinese）

［8］朱敏波．星载大型可展开天线热分析技术研究［D］．西安：西安电子科技大学，2007

Zhu Minbo．Thermal analysis technology study of a large deployable antenna［D］．Xi’an：Xi’an Electronics Science and Technology University，2007（in Chinese）

［9］闫照明．复合材料桁架结构热变形分析［D］．哈尔滨：哈尔滨工业大学，2007

Yan Zhaoming．Thermal deployable analysis of composite material truss structure［D］．Harbin：Harbin Institute of Technology，2007（in Chinese）

［10］李琴，朱敏波．星载大型可展桁架天线热变形分析［J］．计算机辅助工程，2010，19（3）：40-43

Li Qin，Zhu Minbo．Thermal deformation analysis of large deployable truss antenna on satellite［J］．Computer Aided Engineering，2010，19（3）：40-43（in Chinese）