航天器微振动稳态时域响应分析方法

邹元杰 王泽宇 张志娟 葛东明

（北京空间飞行器总体设计部，北京 100094）

1 引言

航天器结构的在轨微振动响应分析对于光学载荷成像质量评估、振动控制措施应用等都是非常重要的［1-4］。这类分析原则上属于结构动力学的范畴，因此，经典的动力学分析理论和方法都适用。然而，航天器在轨的动力学分析有其自身的特殊性：航天器处于自由-自由状态，与发射段的边界条件差异很大；系统基频较低（小于1 Hz）；激励频率可以达到几百赫兹，有限元模型的精细程度超过星箭耦合分析模型。这些特点使得常规的时程积分数值算法在进行时域响应分析时很不方便。具体说来，存在以下两个问题。

（1）由于航天器结构处于自由-自由状态，其动响应必然包含刚体模态和弹性模态两部分的影响。其中，刚体部分的响应由于没有阻尼作用，受载荷作用时会产生整体姿态“漂移”，呈发散状态。在航天器实际在轨工作时，并不会出现这种姿态发散，主要是因为航天器有姿态控制系统的作用，始终维持姿态在小范围内振荡。如果动力学模型中未引入控制系统的闭环作用，进行开环计算，必然出现姿态“漂移”［5-6］。这个问题可以通过在动力学模型中引入控制系统来消除，也可以人为施加一个低频阻尼器，把刚体模态近似看成一个低频的弹性模态，赋予其振荡特性，自然就不会无限发散。然而，第一种处理方式使动力学模型更为复杂，增加了控制的反馈作用，计算量大大增加；第二种方式中低频阻尼器的频率和阻尼选取在很大程度上取决于分析人员的工程经验，只能作为一种近似处理。

（2）弹性模态的位移由两部分组成，其中一部分是伴随自由振动项，其振动频率为弹性模态的阻尼自由振动频率，随着时间的增长呈指数衰减；另一部分是强迫振动项，其振动频率与外载荷频率相同。航天器长期在轨工作时，其响应应该为后一部分。然而采用时程积分进行数值计算时，伴随自由振动项会参与到总响应中。伴随自由振动项的衰减快慢取决于模态阻尼和模态频率的大小。对于航天器微振动响应来说，因为系统的频率（通常取决于大型柔性附件的频率）很低、在轨振动阻尼较小，其衰减时间尤其长。举例来说，假定第j阶弹性模态的阻尼比ξj＝0．003，系统自由-自由状态基频ωj为0．1Hz，若要使伴随自由振动项振幅衰减为初始时刻的5%，令e-ξjωjt＝0．05，可得所需计算时长t＝1589s（约26 min）。对于时域响应的数值计算来说，通常的计算时长为秒级，26 min的计算时间是难以接受的。

本文提出了基于复频理论的时域响应分析方法，可以不引入控制系统而消除刚体姿态“漂移”，并且不需要长时间的计算就能直接得到稳态时域响应结果。

2 微振动稳态时域响应分析理论

结构系统的动力学时域方程为［7］

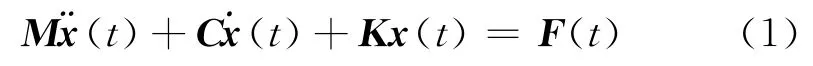
式中：M为质量矩阵；C为阻尼矩阵；K为质量矩阵；F为外载荷向量；x为节点位移向量，t为时间。

利用模态叠加法进行解耦处理，设

式中：Φ和q分别为模态振型集和模态主坐标向量；Φr和Φe分别为刚体和弹性体模态振型集，其中n为弹性模态阶数；qr和qe分别为刚体和弹性体模态主坐标向量，其 中

将式（2）代入式（1），考虑到模态的正交性，且刚体模态刚度阵和阻尼阵为0，可得

再采用质量归一，将式（3）和式（4）的方程解耦后得到

航天器微振动最主要的干扰源为动量轮等活动部件的不平衡力，这类载荷F（t）近似呈正弦波（或余弦波）叠加的形式［3-4］。这样，式（5）和式（6）可以分别表达成以下形式：

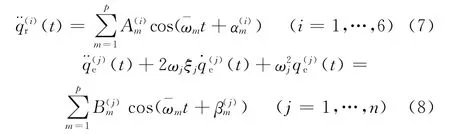
在初始条件qr（0）＝qr（0）＝0，qe（0）＝qe（0）＝0，以及小阻尼假设条件下，式（7）和式（8）的位移解可以分别表达为以下形式：

式中：第j阶弹性模态阻尼自由振动频率分别为第j阶弹性体模态在频率处的瞬态位移响应幅值、以及与激励的相位差，分别为第j阶弹性体模态在频率ωm处的稳态位移响应幅值、与激励的相位差。当然，式（9）、（10）的结果只能通过时域数值计算得到，且激励频率上限越高，需要的计算时间步长越短，花费的总时间越多。

将式（7）、（8）改写成复频域形式：

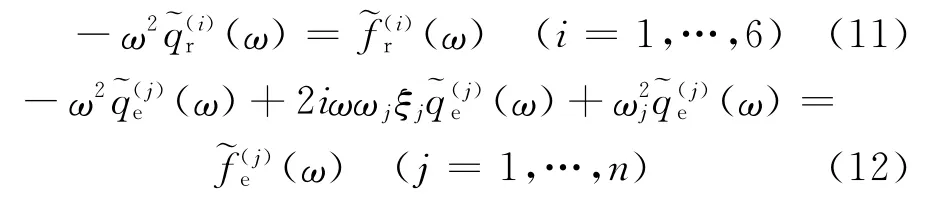
对于任意的离散频率点ω＝ωm，有

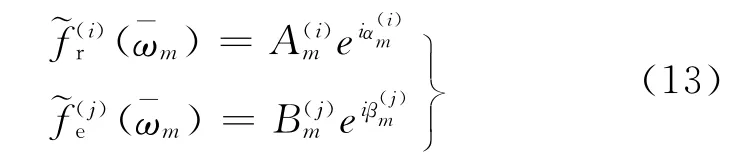
代入式（11）、（12），求解可以得到频域内的模态位移

为了得到稳态的系统时域动力学响应，进而用于成像质量评估，还需要在上述频域计算完成后，获得时域响应结果。这需要首先提取对应各激振频率的响应幅值和相位，而后采用复响应的实部形式表达时域响应，最后将各频率成分进行代数累加。转换后的时域响应为

比较式（16）、（17）与式（9）、（10）可以看出：由复频理论获得的时域响应结果式（16）、（17），正是我们预期获得的对应（9）、（10）两式除去刚体“漂移”和伴随自由振动衰减项后的结果。

上述频域计算只在p个离散的频点上计算，需要花费的时间比时域计算来说小得多，且计算精度很高，不受时域计算步长、不同时程积分算法的影响。因此，本文的方法较时程积分算法有较大的优势。

3 工程应用实例

本节将上述分析理论应用于某航天器（构型示意图及坐标系见图1），计算其在控制力矩陀螺不平衡力（矩）作用下的微振动响应。在分析时，首先应用通用有限元分析软件PATRAN／NASTRAN 建立了航天器有限元模型，并进行了频响分析，而后利用Matlab软件编程实现了频域到稳态时域响应的转换。

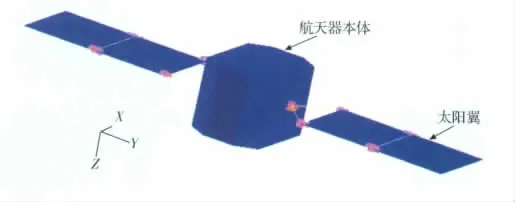
图1 航天器在轨构型的示意图Fig．1 Schematic of spacecraft on-orbit configuration

3．1 系统自由模态分析

为了在计算响应时利用模态叠加法，首先要进行航天器系统在轨自由模态分析。表1给出了9阶模态的分析结果。前6阶模态为系统的刚体模态；7～9阶为太阳翼的弯曲模态。图2～图4为弹性模态的振型图。

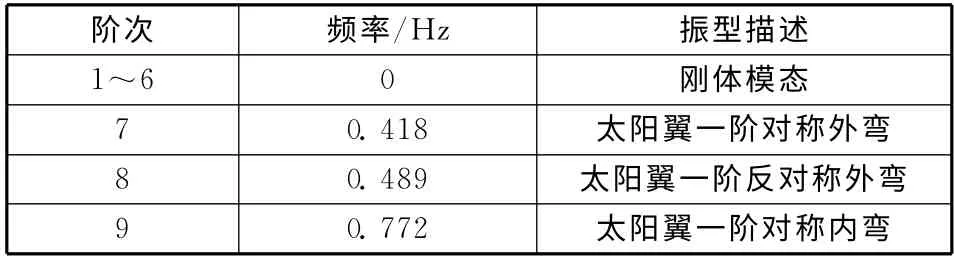
表1 系统模态的振型Table 1 Mode shapes of on-orbit spacecraft

图2 太阳翼一阶对称外弯（绕X 轴）Fig．2 First symmetrical bending mode（X-axis）

图3 太阳翼一阶反对称外弯（绕X 轴）Fig．3 First anti-symmetrical bending mode（X-axis）

图4 太阳翼一阶对称内弯（绕Z 轴）Fig．4 First symmetrical bending mode（Z-axis）

3．2 系统稳态响应分析

计算航天器在控制力矩陀螺不平衡力（矩）作用下相机安装界面的角位移和加速度响应，并统计了积分时间内最大角位移（峰峰值）、角位移均方根值和加速度均方根值。给定的不平衡力矩由一系列谐波构成，各谐波频率与幅值如表2所示。

表2 不平衡力（矩）幅值Table 2 Disturbance force／moment amplitude

分别针对刚体模型、弹性体模型和“刚体＋弹性体”模型的微振动响应进行了计算。计算中选取0～300Hz内的约900阶模态，模态阻尼比取为0．01。

1）刚体模型分析结果

将航天器视为刚体（与式（11）对应），分析其稳态响应，得到相机安装面和扰动源处的位移和加速度。相机安装面角位移的时域曲线、频域曲线（由时域曲线经快速傅里叶变换（FFT）得到）分别见图5和图6。50ms积分时间内角位移峰峰值见表3。

图5 刚体模型的转角位移时域曲线Fig．5 Time-domain rotation displacements with rigid-body model

图6 刚体模型的转角位移频域曲线Fig．6 Frequency-domain rotation displacements with rigid-body model

表3 50ms积分时间内的最大角位移峰峰值（刚体模型）Table 3 Maximum displacements in 50ms integration time with rigid-body model （″）

从图5可以看出，本文所计算的刚体时域响应并无“漂移”现象，即没有出现响应振幅随时间无限增大（如后文中的图9所示）的现象，从根本上解决了常规时程积分算法出现的位移发散问题。从图6可以看出，频谱中较大的响应集中在扰动源的6个激振频率。

2）弹性体模型分析结果

将航天器视为弹性体（与式（12）对应），得出相机安装面和扰动源处的位移和加速度。相机安装面角位移的时域曲线、频域曲线，分别见图7、图8。50ms积分时间内角位移峰峰值见表4。

图7 弹性体模型的转角位移时域曲线Fig．7 Time-domain rotation displacements with flexible-body model

图8 弹性体模型的转角位移频域曲线Fig．8 Frequency-domain rotation displacements with flexible-body model

表4 50ms积分时间内最大角位移峰峰值（弹性体模型）Table 4 Maximum displacements in 50ms integration time with flexible-body model （″）

从图7可以看出，本文所计算的弹性体时域响应已经消除了瞬态效应（即伴随自由振动项）的影响，从时域计算一开始就达到了稳态，而不需要长时间的稳定过程。

对比表4和表3的角位移峰峰值可以看出，对于该航天器在本文给定的扰动源下的微振动响应来说，弹性体模型的角位移比刚体模型高两个量级以上，即在航天器微振动响应时，弹性模态的影响较刚体模态大得多，因此，结构柔性的影响在微振动分析中必须考虑。

3）“刚体＋弹性体”模型的分析结果

同时考虑刚体及弹性体的作用，分析稳态响应。由于该模型的计算结果实质是弹性体模型和刚体模型线性叠加，因此其相应的位移响应曲线与弹性体模型较为接近。此外，计算了加速度响应，统计后的加速度均方根值见表5。加速度响应计算结果表明，从扰动源安装位置到相机安装界面，加速度响应呈下降趋势，说明结构系统对外扰动有一定的衰减作用。

表5 加速度均方根值Table 5 RMS of Acceleration gn

3．3 与传统时程积分法的对比

首先，对比了本文的方法与传统时程积分方法的时域曲线。图9为采用传统时程积分方法计算的相机界面转角位移。对比图9与图5、图7 可以发现，采用传统时程积分方法计算，转角位移时域曲线是在一条直线（本文称为刚体“漂移”）上叠加若干个余弦波，总位移是无限增加的，而本文的方法却直接获得稳态时域响应。

然后，对比了本文的方法与传统时程积分方法的频谱曲线，选取相机界面RY角位移量作为分析对象。图10给出了频谱曲线的对比结果。从图10可以看出，两种方法在激振频率处的响应幅值较为接近，但低频段（一阶共振频率以下）的频谱差别很大。这主要是由于传统时程积分法中刚体“漂移”响应的影响，以及非共振频率处弹性模态响应在5s的计算时间内不能完全衰减的结果。

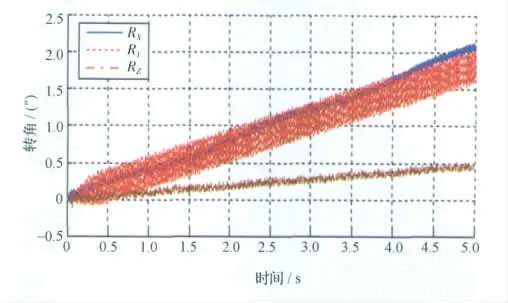
图9 传统时程积分法计算的相机安装界面角位移Fig．9 Rotation displacements for satellite camera calculated with traditional time-integration method

图10 相机界面角位移（RY）的频谱Fig．10 Frequency spectrum of RYfor the camera

最后，计算了积分时间内的相机界面角位移响应的峰峰值，对比了本文的方法与传统时程积分方法的计算结果。

表6给出两种方法的角位移峰峰值对比情况。从表中数据可以看出，当积分时间较长时（如50ms），传统时程积分方法统计出的角位移峰峰值比本文的方法大，如前者RZ峰峰值约为本文方法的2 倍。过于保守的角位移峰峰值估计，必然对光学载荷成像质量评估和设计带来不利影响。此外，随着积分时间的减小，两者的差别也在减小。

表6 积分时间内的最大角位移峰峰值Table 6 Maximum displacements in the integration time

4 结论

本文通过航天器微振动稳态时域响应分析理论和工程应用研究，得到以下结论：

（1）提出的基于复频理论的航天器微振动稳态时域响应分析方法，同传统的时程积分方法比较，对于谐波形式干扰源作用下的航天器微振动时域响应计算，可以完全消除刚体“漂移”和弹性体瞬态效应的影响，直接获得稳态时域响应，应用也非常简便。

（2）航天器微振动响应包含刚体运动和弹性变形两部分的影响，其中弹性体变形引起的响应占主要成分。

（3）相机安装界面处的加速度响应小于扰动源安装位置的加速度，说明结构对扰动的传递起到了一定的衰减作用。

（4）对于较长的积分时间，传统时程积分法可能给出较为保守的角位移峰峰值，这给光学载荷成像质量评估和设计带来不利影响。随着积分时间的减小，传统时程积分法计算的响应峰峰值与本文方法的差别有减小的趋势。

（References）

［1］Gutierrez H．Performance assessment and enhancement of precision controlled structures during conceptual design［D］．Cambridge：Ph．D．Dissertation of Massachusetts Institue of Technology，1999

［2］Liu K，Maghami P．Reaction wheel disturbance modeling，jitter analysis，and validation tests for solar dynamics observatory，AIAA 2008-7232［R］．Washington：AIAA，2008

［3］Mosier G E，Howard J M，Johnston J D，et al．The role of integrated modeling in the design and verification of the james webb space telescope［J］．SPIE，2004：96-107

［4］LoBosco D M，Blaurock C，Chung Soon-Jo，et al．Integrated modeling of optical performance for the terrestrial planet finder structurally connected interferometer［J］．SPIE，2004：278-289

［5］葛东明，邹元杰，张志娟，等．基于全柔性卫星模型的控制闭环微振动建模与仿真［J］．航天器工程，2012，21（5）：58-63

Ge Dongming，Zou Yuanjie，Zhang Zhijuan，et al．Control closed-loop micro-vibration modeling and simulation based on flexible satellite model［J］．Spacecraft Engineering，2012，21（5）：58-63（in Chinese）

［6］张志娟，邹元杰，关晓东，等．基于柔性多体理论的遥感卫星颤振分析方法研究［C］／／高分辨率遥感卫星结构振动及控制技术研讨会．北京：中国宇航学会，2011：329-335

Zhang Zhijuan，Zou Yuanjie，Guan Xiaodong，et al．Study on remote sense satellite jitter based on flexible multi-body theory［C］／／Symposium on Structure Vibration and Control Techniques for High Revolution Remote Sense Satellite．Beijing：Chinese Society of Astronautics，2011：329-335（in Chinese）

［7］邹经湘，于开平．结构动力学［M］．2版．哈尔滨：哈尔滨工业大学出版社，2009

Zou Jingxiang，Yu Kaiping．Structure dynamics［M］．2nd ed．Harbin：Press of Harbin Institute of Technology，2009（in Chinese）